關于圓切線的考向例析與探究思考

顧亞平

[摘? 要] 圓切線是初中幾何的重點，其性質、定理也是常考知識. 分析近幾年的中考試題會發現，中考試題題型靈活，考查知識點多，綜合性強，對學生的知識綜合運用能力及思維能力有著較高的要求，所以結合考查方法對圓切線內容加以探究有著重要的意義. 文章結合實例對幾個圓切線常見考查視角進行探討，提出相應的建議.

[關鍵詞] 圓切線;考向;性質;判定;三角形;翻折

圓是初中數學的核心圖形，含有眾多的考點，其中與圓切線相關的定理既是中考考查的重點，又是幾何問題突破的關鍵. 而切線的考查方向及視角較為多樣，下面結合實例對圓切線的考向進行探究.

關于圓切線的考向舉例

圓切線的概念相對容易理解，但切線背后隱含了幾何數量關系和位置關系，由切線所構成的直角更是特殊圖形形成的基礎. 中考對圓切線的考向較多，其中有如下幾個重要方向：圓切線的計算及證明、三角形的內切圓、切線性質的推理與計算.

1. 切線的計算及證明

論證圓切線的關系有多種考查方式，通常有如下兩個方向：一是從動點角度命題，直接考證圓運動過程中與直線的交點;二是從量的角度出發，偏重與圓相切時隱含的數量關系. 但無論如何命題，考查切線的判定定理這一本質是不變的，只需要充分結合切線的判定方法來構建思路即可.

例1? （2019年遂寧中考卷）如圖1，△ABC內接于⊙O，直徑AD交BC于點E，延長AD至點F，使DF=2OD，連接FC并延長交過點A的切線于點G，且滿足AG∥BC，連接OC. 若cos∠BAC= ，BC=6.

（1）求證：∠COD=∠BAC;

（2）求⊙O的半徑OC的長;

（3）求證：CF是⊙O的切線.

解析? 此處主要剖析第（3）問，證明OC⊥GF或∠OCF=90°即可. 直接進行角度推導存在一定的難度，可在圖形中提取相似三角形. 已知Rt△COE，若能證明△COE與△FOC相似，即可直接推導出∠OCF=∠OEC=90°，即CF是⊙O的切線，過程如下.

因為DF=2OD，所以OF=3OD=3OC. 所以 = = . 又∠COE=∠FOC，所以△COE∽△FOC. 由相似三角形的性質可得∠OCF=∠OEC=90°. 所以CF是⊙O的切線.

評析? 切線的計算及證明，實質就是考查圓相切關系的證明方法. 相切意味著垂直，故可通過角度推導和三角形邊長關系分析來加以論證. 該考查方向還可以綜合三角形相似、勾股定理、三角形全等等知識.

2. 三角形的內切圓

三角形的內切圓是考查圓切線的另一特殊考向. 三角形的內切圓與三角形的三條邊均相切，此時的圓心為三角形的內心. 分析圖像可知，圓心到三角形三邊的距離相等，深入分析可將其與角平分線的性質相關聯，故該考向主要考查三角形內切圓的性質、角平分線的性質等.

例2? （2019年興化期末卷）如圖2，△ABC的周長為20 cm，BC=6 cm，△ABC的內切圓為⊙O，MN是⊙O的切線，MN與AB相交于點M，與CA相交于點N，則△AMN的周長為______.

解析? 題干設定△ABC的內切圓為⊙O，則圓心O到△ABC三條邊的距離相等. 同時可在圖形中提取角平分線，獲得相應的全等三角形，進而進行等線段轉化，完成△AMN的周長求解，具體如下.

過點O分別作AB，BC，AC和MN的垂線，垂足分別為E，F，D，G，連接BO. 分析可知OF=OE，顯然BO為∠FBE的平分線，進而可證△FBO≌△EBO. 由全等性質可得BE=BF. 同理可得CF=CD，DN=NG，EM=GM，AD=AE. 因為△ABC的周長為20 cm，BC=6 cm，所以可推得AE=AD=4. 所以△AMN的周長=AM+AN+MN=AE+AD=8.

評析? 三角形的內切圓問題涉及角平分線、三角形全等等知識，利用其中的等角和全等圖形可完成等線段轉化，因此，其中的周長問題實則就是等線段轉化問題. 可見，理解考向的本質是解題突破的關鍵.

3. 切線性質的推理與計算

切線性質的推理與計算是常見的考查方向，雖考點一般，但其中涉及的知識點較多，通常融合了三角函數，圓周角、圓心角、弧、弦之間的關系，深刻理解切線的性質，充分利用其性質進行關聯轉化是問題突破的關鍵.

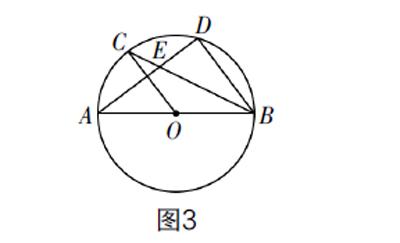
例3? （2019年成都中考卷）如圖3，AB是⊙O的直徑，C，D為⊙O上的兩點，OC∥BD，弦AD，BC相交于點E.

（1）求證： = ;

（2）若CE=1，EB=3，求⊙O的半徑;

（3）在（2）的條件下，過點C作⊙O的切線，交BA的延長線于點P，過點P作PQ∥CB交⊙O于F，Q兩點（點F在線段PQ上），求PQ的長.

解析? 上述與圓相關的問題涉及證明弧長相等、求圓半徑長和求線段長三大問題，分析時需要充分利用圓的性質.

（1）等弧所對的圓周角相等，只需證明∠OBC=∠CBD即可. 由于OC=OB，所以∠OBC=∠OCB. 又OC∥BD，所以∠OCB=∠CBD. 所以∠OBC=∠CBD. 所以 = .

（2）求⊙O的半徑可先求直徑AB，連接AC，則∠ACB=90°. 分析可知BC=4，△ACE∽△BCA，由相似性質可得 = ，則AC2=CB·CE=4. 所以AC=2. 在Rt△ACB中，由勾股定理可得AB= =2 ，所以⊙O的半徑為 .

（3）根據題干信息作圖，再過點O作PQ的垂線，垂足為H，如圖4. 因為PC是⊙O的切線，所以∠PCO=90°. 所以∠PCA=∠BCO=∠CBO. 又∠CPB=∠CPA，所以△APC∽△CPB. 由相似性質可得PC=2PA，PC2=PA·PB，所以PA= ，PO= . 分析可證△PHO∽△BCA，由相似性質可得 = = ，可解得PH= ，OH= ，所以HQ= = . 所以PQ=PH+HQ= .

評析 上述求證弧長相等及求線段長，考查了切線性質等與圓相關的知識，其中相似三角形的性質、勾股定理是本題思路構建的關鍵. 因此，對于圓切線的綜合性問題，應關注復合圖形的特點，充分利用特殊圖形及特殊關系來進行線段、角度的轉化.

4. 幾何翻折與圓切線

幾何翻折是初中幾何的重點內容，圓切線知識也可與幾何翻折聯合起來考查. 解析時需要充分理解圖形翻折的過程，利用翻折過程中“變”與“不變”的量、圓的切線性質來剖析圖形、構建思路.

例4? 如圖5，AB為⊙O的直徑，點C在⊙O上，現將 沿著直線BC進行翻折，恰好 的中點D落在圓心O處. 連接OC，CD，BD，過點C的切線與BA的延長線交于點P，連接AD，于PB的另外一側作∠MPB=∠ADC.

（1）分析PM與⊙O的位置關系，并簡述理由;

（2）若PC= ，試求四邊形OCDB的面積.

解析? （1）連接DO并延長交PM于點E. 根據折疊性質可得OC=DC，BO=BD，又BD=CD，所以四邊形OBDC為菱形. 由菱形性質可得OD⊥BC. 又OD=OC=OB，所以△OCD和△OBD均為等邊三角形. 所以∠COP=∠EOP=60°. 通過證明PM∥BC得到OE⊥PM，進一步推得OE= OP，根據切線的性質可得OC⊥PC，且有OC= OP，故OC=OE，從而可判定PM是⊙O的切線.

（2）在Rt△OPC中，OC= PC=1，所以四邊形OCDB的面積=2S =2× ×12= .

評析? 本題的翻折背景中涉及圓切線的性質，由切線中的垂直關系來構造圖形是突破的關鍵. 綜合考查折疊、圓切線性質、圓周角定理也是中考的重點考向，在復習階段應重視對幾何知識的整合，提升解題的綜合能力.

關于圓切線考向的學習建議

1. 挖掘定理，串聯定理

圓切線的判定、性質定理雖內容較為簡單，但在學習時應深入挖掘定理內涵，理解其中的知識原理，如圓與線段相切中隱含著如下特殊關系：數量關系——圓半徑與圓心到切線的距離相等，垂直關系——切線和圓心與切點的連線垂直. 而對于切線判定定理，則應把握其中的條件，包括公共點、垂直關系等. 定理之間并不是獨立存在的，學習幾何定理時還應聯系前后知識加以串聯，關注圓切線與角平分線性質、勾股定理、圓周角定理等定理之間的聯系，建立完整的定理體系，為后續綜合問題的突破奠定基礎.

2. 考向綜合，技能提升

圓的性質定理是中考的重點，上述例子探討了圓切線性質定理的主要考向，其中包括基本的相切論證、線長推斷，也涉及綜合性的三角形與圓內切、翻折與圓切線. 從考查內容來看，涉及相似性質、全等性質、勾股定理、角平分線性質、三角函數、翻折特性等，這些內容是平面幾何的核心，因此對于該部分的學習需要立足基礎，綜合知識，發展思維. 同時，圓切線問題的解決離不開輔助線，合理添加輔助線有助于挖掘圓內特性，有利于解題思路的構建，因此應掌握圓切線問題中輔助線添加的技巧，增強作圖能力，促進綜合素養的提升.

總之，圓切線的考向較多，充分理解定理、把握知識關聯、關注問題類型、總結解題技巧是該內容學習的關鍵. 另外，圓切線問題的求解中滲透著數學思想，合理利用數形結合、模型思想、轉化思想可提高解題效率，故應重視思想方法的學習，綜合提升解題能力.