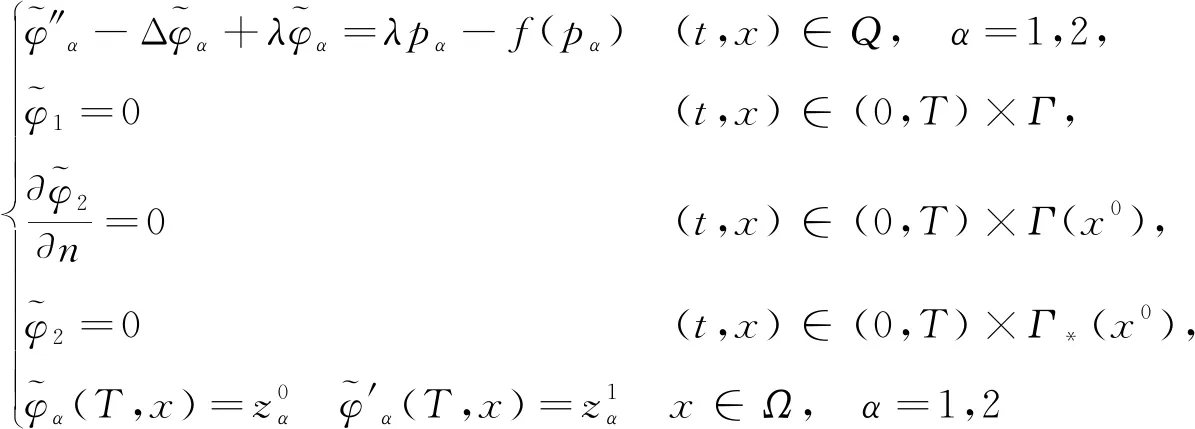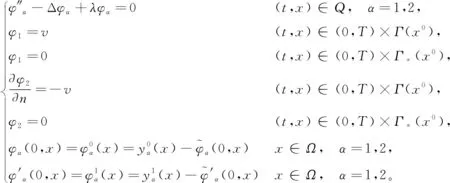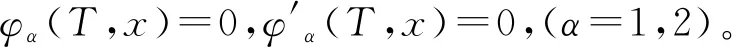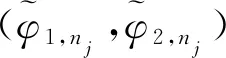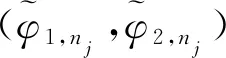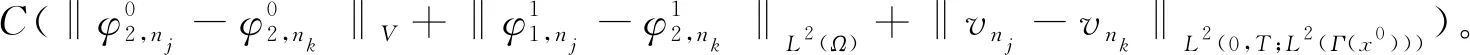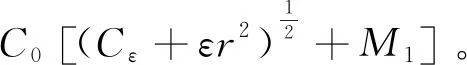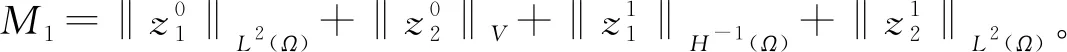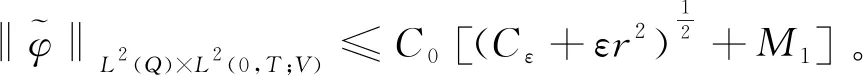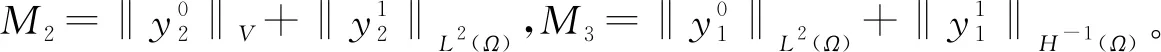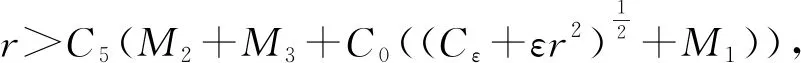兩個非線性波方程的同時邊界控制
武潔瓊,張宏偉
(山西大學 數(shù)學科學學院,山西 太原 030006)
0 引言
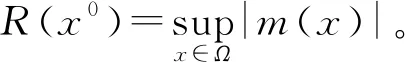
考慮下述問題
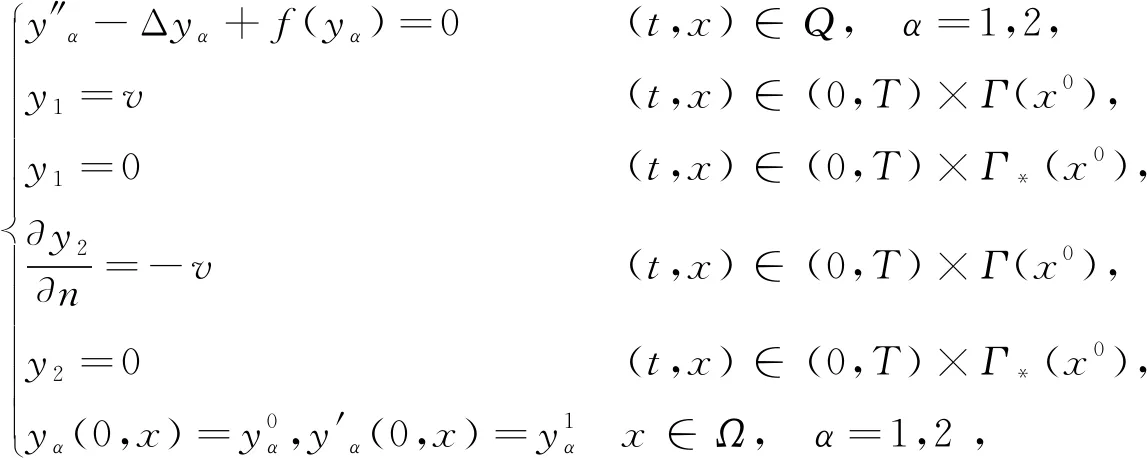
(1)
其中v是邊界控制函數(shù),f∈C1(R)是一個非線性函數(shù)并且滿足:存在常數(shù)C>0和σ>0使得
|f(s)-f(r)| (2) 和 (3) 從(3)易得任給ε>0,存在Cε>0使得 |f(s)-λs|≤Cε+ε|s|, ?s∈R。 (4) 注意到在(1)中有兩個受控系統(tǒng),一個是具有Dirichlet邊界控制的波動系統(tǒng),另一個是具有Neumann邊界控制的波動系統(tǒng)。考慮是否可用同一個控制函數(shù),使得系統(tǒng)(1)的兩個波動方程都精確能控,也就是系統(tǒng)(1)的同時能控性問題。 令 V={φ|φ∈H1(Ω),φ(x)=0, ?x∈Γ*(x0)}。 (5) “同時精確能控性”這個概念是Russell[1]在研究矩形區(qū)域中Maxwell方程的能控性時首先提出的。文獻[1]中,作者將Maxwell方程的能控性問題轉(zhuǎn)化成兩個解耦波方程的同時能控性,其中一個波方程具有Dirichlet邊界控制,而另一個具有Neumann邊界控制。Lions[2]研究了線性解耦波方程組的同時精確能控性,即(1)中的f(·)≡0。關(guān)于波動方程的同時內(nèi)部能控性,已有不少文獻,如文[3-6]。利用唯一延拓性,Haraux[3]證明了矩形區(qū)域中一維波的內(nèi)部同時精確能控性。文獻[4-5]分別討論了線性和非線性解耦波方程的同時精確能控性,其中非線性項f滿足式(2)與(3)。利用不動點理論,文獻[5]得到了系統(tǒng)的內(nèi)部同時能控性。文獻[4-5]的波動系統(tǒng)均是無阻尼系統(tǒng),文[6]研究了幾個阻尼波系統(tǒng)的同時內(nèi)部精確能控性。關(guān)于波方程能控性的研究還可見文[7]。文[8]研究熱彈性板的同時精確和近似能控性。文獻[9]研究了兩個抽象系統(tǒng)(其中一個是有限維系統(tǒng)而另一個是無限維系統(tǒng))的同時精確能控性。文[10]研究帶有約束條件的同時能控性并給出在同時辨識方面的應用。 注意到,關(guān)于帶有滿足條件(2)-(4)的非線性外力源的非線性波動系統(tǒng)的邊界同時精確能控性還沒有研究成果。這篇文章做這方面的工作。 為方便起見,先引入如下記號。令μ0是使得下式成立的常數(shù): (6) (7) 本文的主要結(jié)論如下: (8) 對于任意的p1∈L2(Q)與p2∈L2(0,T;V),引入一個線性系統(tǒng) (9) 在這一節(jié),將證明系統(tǒng)(9)是同時精確能控的,即 (10) 為證明定理2,先證明一個觀測性不等式。為此,引入(9)的對偶系統(tǒng) (11) 系統(tǒng)(11)的能量定義為 (12) 定理3設T>T(x0),則(11)的解滿足 (13) 證明先證明 (14) 在(11)的主方程兩邊乘以m·φα,α=1,2,在Ω×(0,T)上積分,然后相加,得 (15) (16) 下面估計(16)中各項。由(6)和E0的定義,我們有 (17) 此外,有 (18) 和 (19) 所以由(16)-(19),得 (20) (21) 結(jié)合(20)與(21),我們得到(14)。 假設χ滿足 (22) 令 (23) 則下述方程成立 (24) 當T充分大時,由(14)可得 (25) 其中 (26) 定理2的證明令(Ψ1,Ψ2)滿足 (27) 我們定義映射Λ∶F→F′如下 (28) F的范數(shù)定義為 (29) 由不等式(13)和Lax-Milgram定理可得Λ是從F到F′的同構(gòu)映射,因此系統(tǒng)(9)是精確能控的。 這一節(jié)將用Schauder不動點定理證明定理1。 定理1的證明令p=(p1,p2)∈L2(Q)×L2(0,T;V),考慮下面的偏微分方程(PDE)系統(tǒng) (30) 和控制系統(tǒng) (31) 要完成定理1的證明,只需證明K有不動點。下面先證明K是連續(xù)映射。假設(pn)在L2(Q)×L2(0,T;V)中收斂于p。將證明點列(K(pn))在L2(Q)×L2(0,T;V)中收斂到K(p)。由Riesz定理,在(pn)中存在子列(pnj)使得(pnj(x,t))幾乎處處收斂到p(x,t)。由(4)和廣義勒貝格控制收斂定理,得(f(pnj))在L2(Q)×L2(0,T;V)中收斂到f(p)。 由波方程解的正則性[11],得 C‖λp1,nj-f(p1,nj)-λp1,nk+f(p1,nk)‖L2(Q) (32) 和 C‖λp2,nj-f(p2,nj)-λp2,nk+f(p2,nk)‖L2(0,T;V)。 (33) 下面證明映射K2的連續(xù)性。當α=1時,由文[12]中的定理2.5,我們有 (34) 下面考慮(vnj)。因為Λ是一個同構(gòu)映射,由(31)得 ‖vnj‖L2(0,T;L2(Γ(x0)))≤ (35) 因此(vnj)是L2(0,T;L2(Γ(x0)))上的柯西列,并且收斂到函數(shù)v。 當α=2時,利用文獻[12]中的定理4.7,可得 (36) 用相似的方法,知(φ2,nj)是柯西列。因此,(φ1,nj,φ2,nj)在L2(Q)×L2(0,T;V)中收斂到(31)關(guān)于p的解φ=(φ1,φ2)。故映射K2是連續(xù)的。因此,映射K是連續(xù)的。 令r>0,Br={z∈L2(Q)×L2(0,T;V);‖z‖L2(Q)×L2(0,T;V)≤r}。我們將證明?p∈Br,(9)滿足(8)的解y仍屬于Br。由(4)知?ε>0, (37) 由波方程解的正則性和(37)可得?ε>0, (38) 則由(38)可得 (39) 對于‖φ‖L2(Q)×L2(0,T;V),利用波方程解的正則性,得 (40) 和 (41) (42) 結(jié)合(39)與(42),得 (43)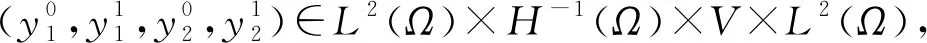
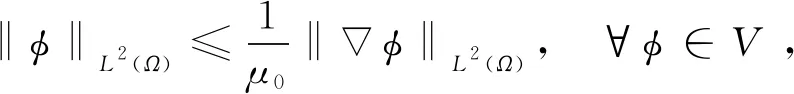
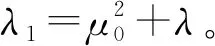

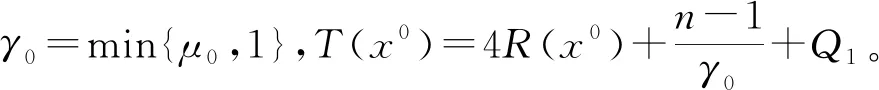
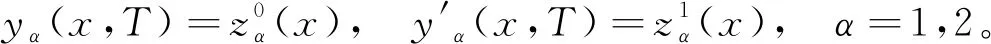
1 線性化系統(tǒng)
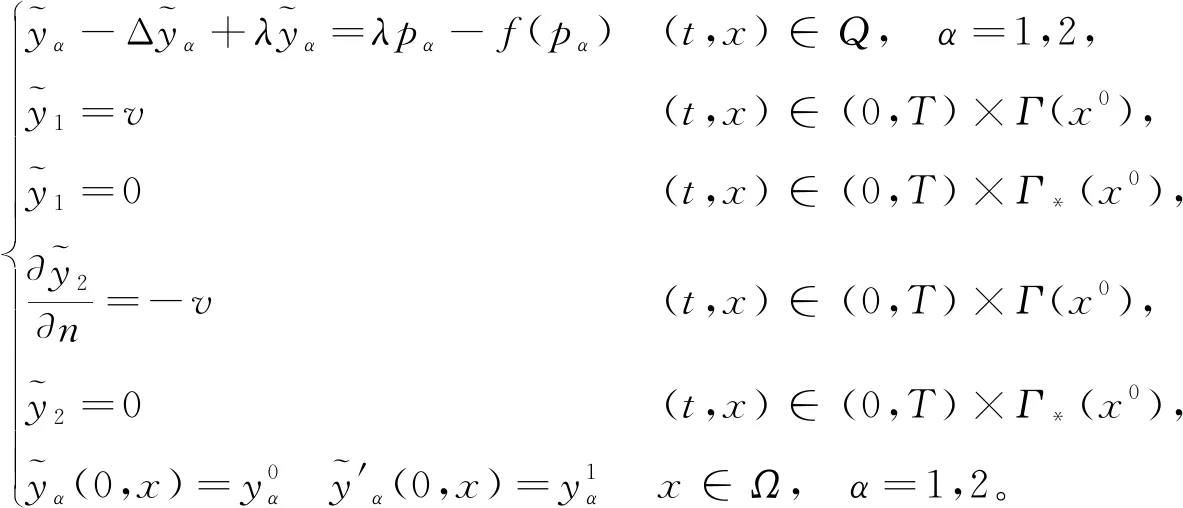
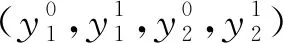
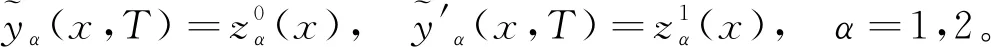
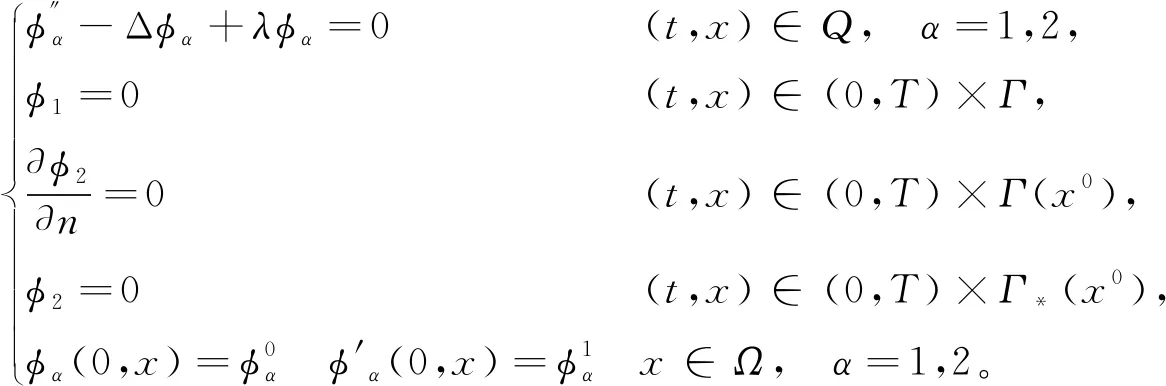
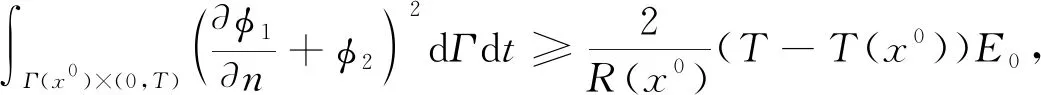
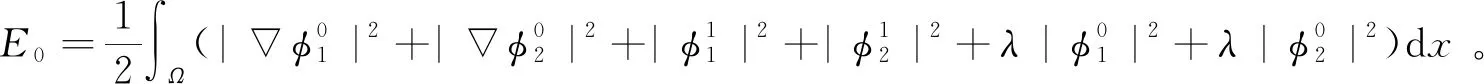

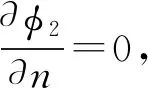
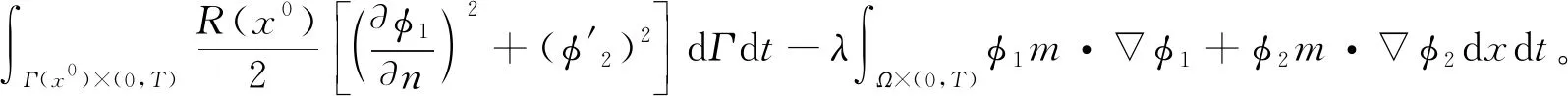

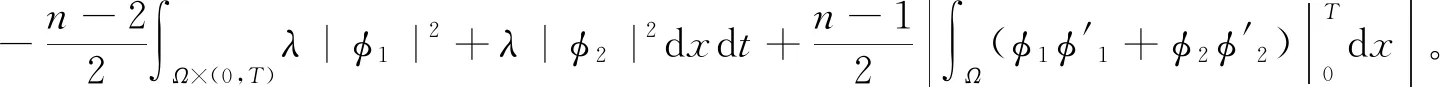
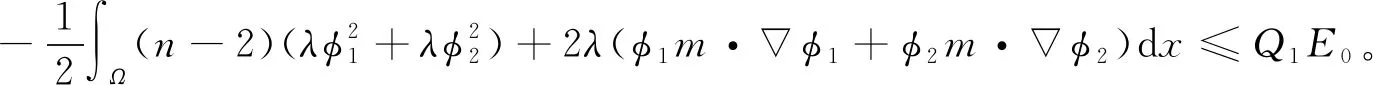
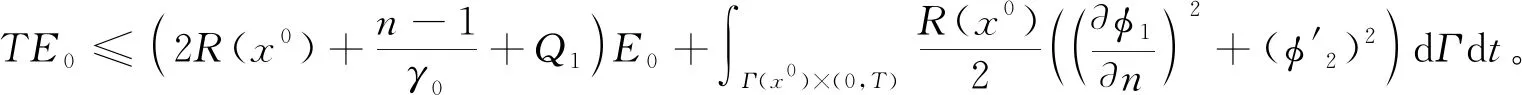
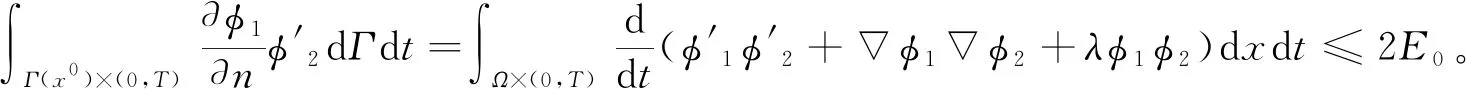
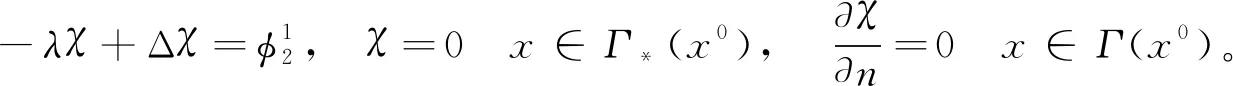
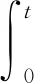
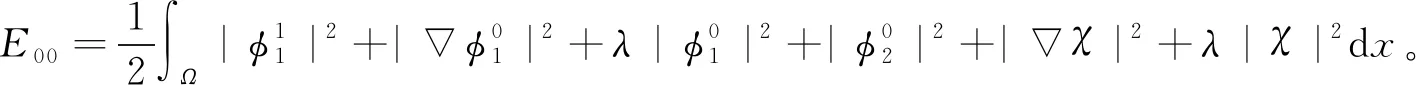
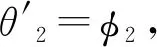
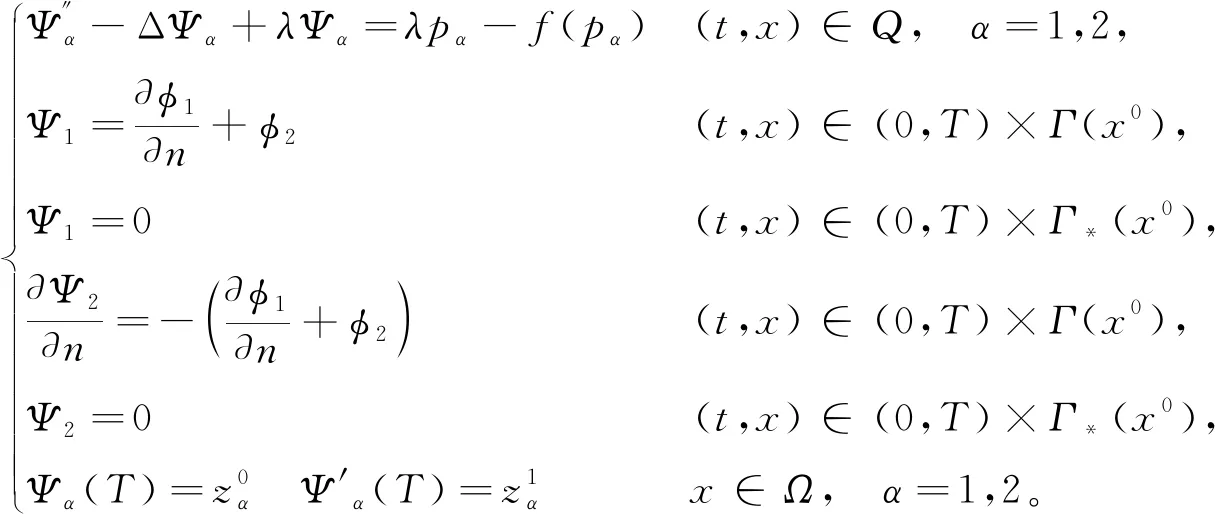
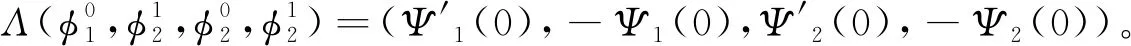
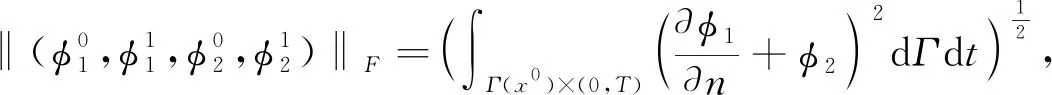
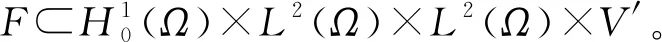
2 非線性系統(tǒng)