向量值子空間上弱Gabor對偶超標架的刻畫

賈慧芳,蔡婉亭

(山西大學 數學科學學院，山西 太原 030006)

0 引言

標架的概念是1952年Duffin和Schaeffer在研究非調和傅里葉級數時提出的[1]。1946年,Gabor在L2()中引入了Gabor系的概念[2]。對其嚴格的數學分析開始于Janssen在1980 年左右的系列論文[3-4]。近年來，Gabor標架理論在圖像識別和信息處理等領域有廣泛的應用[5-7]。向量值空間上的標架也稱為超標架,超標架的概念是由Balan[8]和Han等[9]引入的。因其在多路復用技術領域有廣泛的應用價值,超標架引起了眾多數學學者和工程專家的關注。現有的關于超標架的理論研究大都集中于L2(,L)和l2(S,L)上的小波標架和Gabor標架[10-15]。在實際應用中，我們常常需要處理的信號是落在某個子空間上的。此時我們希望在保留觀測數據全部特征的同時,能以更有效的方式來進行信號的Gabor分析或小波分析[16-21]。

設H是一個可分的希爾伯特空間,{ei}i∈I是H中的至多可數序列。若存在兩個正的常數C1,C2使得：對任意的f∈H,均有不等式

(1)

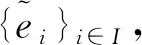
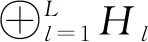
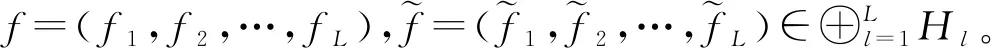
supp(f)={x∈:f(x)≠0}

顯然，在相差一個零測度集的意義下,它是唯一確定的。對f∈L2(,CL),定義調制算子Mx0和平移算子Tx0如下(x0∈):

Mx0f(·)=(e2πix0·f1(·),e2πix0·f2(·),…,e2πix0·fL(·)),

Tx0f(·)=(f1(·-x0),f2(·-x0),…,fL(·-x0))。

顯然,這兩個算子都是酉算子。對任意實數α>0,我們稱上的任一正測度集S是α-周期的,是指對任意的n∈,有S+nα=S。給定這樣的周期集S,我們定義L2(S,L)為：

L2(S,L)={f∈L2(,L):supp(f)?S},

易知它是L2(,L)的一個閉子空間。對g∈L2(,L),定義由g生成的Gabor系為:G(g,α,β)={MmβTnαg:α,β>0,m,n∈Z}。如果G(g,α,β)構成L2(,L)上的超標架,則稱其為L2(,L)的Gabor超標架。兩個Gabor系(G(g,α,β)，G(h,α,β))稱為L2(S,L)的一組Gabor對偶超標架是指：G(g,α,β)和G(h,α,β)是空間的兩個超標架且滿足對任意的f∈L2(S,L),有：

下面我們引入L2(S,L)上弱Gabor對偶超標架的定義:

定義1給定g,h∈L2(S,L),(G(g,α,β)，G(h,α,β))稱為L2(S,L)的一組弱Gabor對偶超標架是指存在L2(S,L)的一個稠子集V,使得對任意的有：

其中上述級數是絕對收斂的。此時我們也把(G(g,α,β)，G(h,α,β))稱為L2(S,L)上一組與V相關聯的弱Gabor對偶超標架。

注若G(g,α,β)和G(h,α,β)都是L2(S,L)上的超Bessel序列,那么(G(g,α,β)，G(h,α,β))是L2(S,L)上的Gabor對偶超標架。因此,弱Gabor對偶超標架是Gabor對偶超標架的推廣。

給定α>0, 且S是上的α-周期子集。記

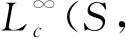
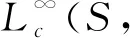
1 輔助引理

本節將給出一些輔助引理,以便為后面的證明作鋪墊。

引理1給定g∈L2(,L)及,L)，則有

(2)

且對任意的m∈,有

〈f,Mmβg〉。

(3)

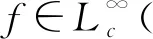
(4)

進而可得

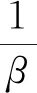
證畢。

引理2給定β>0,以及g,h∈L2(，L),則對任意的，L)有：

(5)

其中左端的級數是絕對收斂的。

證明根據引理1,我們可得對任意的m∈,有：

〈f,Mmβg〉=

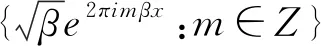
記

則上式可寫成：

根據(2)式,我們易有

由Lebesgue控制收斂定理,可得：

證畢。

引理3給定α,β>0,以及g,h∈L2(,L),則對任意的,L)有：

(6)

其中上述左端的級數是絕對收斂的。

(7)

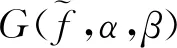
〈f,MmβTnαg〉=〈M-mβT-nαf,g〉,

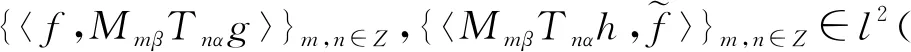
(8)

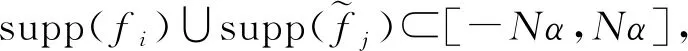
因此，由(8)式可得(6)式成立。證畢。

2 主要定理

定理1給定α,β>0,以及S是上一個α-周期子集。假設g,h∈L2(S,L),則有(G(g,α,β)，G(h,α,β))是L2(S,L)上一組與L∞(S,L)相關聯的弱Gabor對偶超標架等價于對所有的l∈,1≤i,j≤L及有：

(9)

成立。

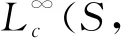
(10)

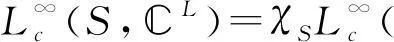
(11)

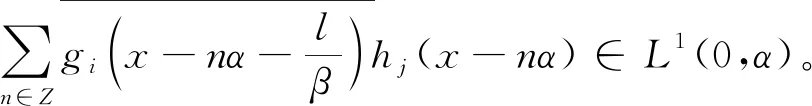
因此,(0,α)上幾乎處處的點都是

的Lebesgue點。結合零測度集的性質,對任意的1≤i,j≤L,l∈,固定x0為

和χS(x)的Lebesgue點。當i≠j時,固定l0∈,1≤i0≠j0≤L,對取,L)滿足：

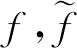
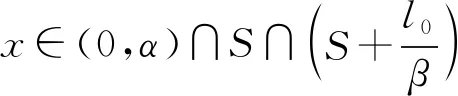
(12)

當i=j時,不妨設i=j=i0，固定l0∈, 1≤i0≤L,對取,L)為：

代入(11)式可得：

根據Lebesgue點的定義,令ε→0,我們可有:

(13)

綜合(12)式和(13)式,根據x0,l0,i0的任意性,我們可得(9)式成立。證畢。

注：該定理推廣了文獻[23]中的定理3.1。這一推廣是非平凡的,因為向量值子空間上的內積結構幾何性質較復雜。