傳統礦柱安全系數計算公式優化研究①

黃 敏， Kulatilake P H S W， 羅嗣海， 方偏桃， 趙聰聰

（1.江西理工大學 資源與環境工程學院，江西 贛州341000； 2.長沙礦山研究院有限責任公司，湖南 長沙410012； 3.金屬礦山安全技術國家重點實驗室，湖南 長沙410012； 4.亞利桑那大學 巖體模擬與計算力學實驗室，美國 亞利桑那州 圖森85721）

礦產資源的地下開采是一個長期的過程，在采掘生產過程中，許多礦山形成了大量的采空區。 據2015年長沙礦山研究院有限責任公司對全國4 606 家地下非煤礦山的統計調查表明，超過50%的地下非煤礦山以空場法進行采礦，形成采空區規模約12.8 億立方米，其中未經處理的空區約占80%。 大量未處理的采空區危害著礦山的后續開采，采空區誘發的冒頂、片幫等事故屢見不鮮，更有甚者引發大面積坍塌、巖移，直至地表塌陷，時刻威脅著礦山工作人員的生命及財產安全，采空區災害已經成為我國分布最廣泛、且危害最大的礦山災害類型之一［1-3］。 而對于如此巨大的空區體積，短期內不可能全部完成治理。 因此，為緩解空區治理壓力，同時確保井下生產安全，對采空區進行穩定性分析十分必要。 對于空場法開采的礦山，頂板與礦柱是維持地下空區穩定的兩大結構單元，國內外學者對于空區的穩定性研究也主要針對這兩方面展開。 對于頂板較為穩固的空區，礦柱的穩定與否更是對空區的支撐有著決定性作用。 礦柱不僅用于維護礦房的穩定，也用于隔離大面積空場，同時還肩負著保護井巷、地表及建筑物的安全作用。 為了保持采場長時間的穩定狀態，保證井下生產工作的安全有序進行，在進行開采設計時，相鄰礦柱的間距必須保證在頂板極限跨度之下，礦柱本身的橫斷面尺寸也必須滿足強度要求［4］，以免因礦柱尺寸太小而無法承受其上覆荷載，導致礦柱被壓垮。 礦柱一旦被壓垮，其上覆巖層荷載將重新分布，該礦柱所承載的巖層質量將由其相鄰的其他礦柱來承擔。 因此，本文主要針對礦柱穩定性展開深入研究，可為類似工程提供技術參考。

1 礦柱穩定性研究現狀

早期對采空區穩定性的研究主要靠礦山工作人員的經驗積累，近年來，隨著巖石力學研究不斷深入和科學技術發展，特別是現代檢測手段及計算機模擬分析技術被廣泛應用于空區穩定性研究，并取得了良好效果，極大地豐富了關于空區穩定性的理論研究與工程實踐［5］。 礦柱穩定性主要取決于礦柱自身強度和礦柱所承受的上覆巖層荷載。 對礦柱穩定性進行分析，其關鍵是對礦柱自身強度和上覆巖層荷載的正確計算［6-8］。 經過長時間的發展，國內外眾多學者在這一方面作了許多研究，并總結了相關理論，包括壓力拱理論、概率密度函數法、兩區約束理論和面積承載理論等，同時在大量室內實驗和工程實踐的基礎上，得到了多種關于礦柱強度的計算公式，主要有安全系數法、理論分析法、數值模擬法等。 其中，安全系數法能定量地對礦柱穩定性進行評價，且簡單實用，因此被廣泛應用于工程實際。

1.1 礦柱所受荷載

礦柱的平均應力取決于在單位面積內礦柱所承受的荷載。 國內外對于礦柱荷載的研究由來已久，也提出了多種假設與理論，目前具有代表性的主要有普氏平衡拱理論、有效區域理論、兩區約束理論及面積承載理論等。

1.1.1 普氏平衡拱理論

普氏平衡拱理論基于自然平衡拱存在，坑道開挖過后，在無支護措施的情況下，坑道頂部會發生巖體自然冒落現象，直至形成一個短時間內保持相對平衡的拱形，稱為平衡拱。

基于普氏拱的礦柱的承載機理如圖1 所示。 巖體開挖后，采空區內的承壓礦柱受到上覆巖層施加的自重應力，頂板巖層出現下沉位移，形成一定范圍的免壓拱，隨著回采的進行，相鄰礦柱上部所形成的免壓拱會發生鏈接，形成一個位于所有采空區礦柱頂部的大免壓拱，即在采空區的上部會產生一個半徑為Rp的免壓拱塑性區。 塑性區的范圍不僅受到巖體性質、開采斷面的影響，還與采空區的埋深有關。 礦體開挖后，采空區的頂板圍巖中會產生一個普氏拱，只要礦柱能承受頂板圍巖免壓拱塑性區范圍內巖體的自重應力，就能保證長期穩定。

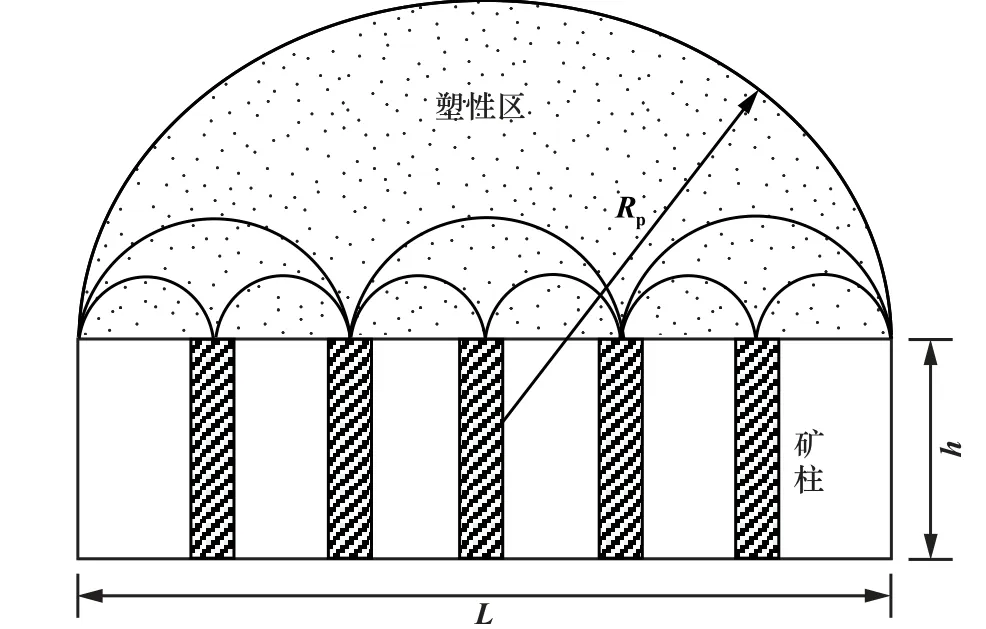
圖1 基于普氏理論的礦柱承載機理分布

根據普氏拱理論和礦柱承壓機理可知，礦柱所承受的荷載為其頂板上方塑性區范圍內所有巖體的重力之和，可計算出免壓拱中塑性區的半徑Rp為：

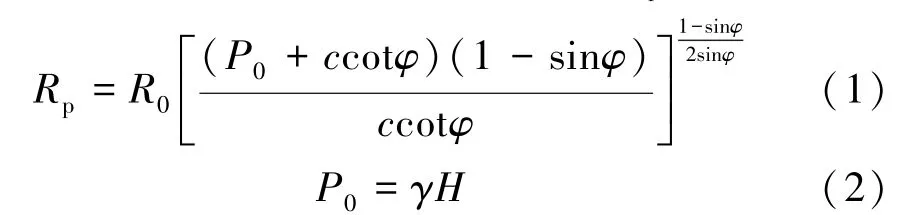
式中R0為開挖半徑，m；P0為開挖處的垂直自重應力，MPa；c為巖體內聚力，MPa；φ為巖體內摩擦角，（°）；γ為上覆巖層巖石容重，kN/m3；H為開采深度，m。

在任何一種情況下，礦柱寬高比都會對礦柱強度產生“尺寸”效應。 單個分層中的礦柱可采用平均應力進行受力平衡分析［9］。 在分層中設計礦柱尺寸時應該考慮礦柱中的峰值壓應力集中。 事實上，在單層礦柱設計方法中，基于平均壓力的設計方法而非峰值應力應用最為廣泛。 礦柱設計的面積承載方法是基于簡單的力學平衡分析，如圖2 ～3 所示，當采場力學平衡時，要求底板對礦柱向上的力Fp等于上覆巖層荷載W，即：

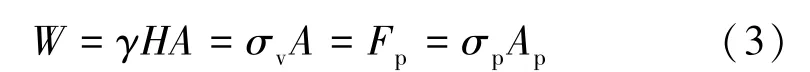
式中σv為平均上覆巖層應力，MPa；A為礦柱所承載巖柱的橫截面積，m2；σp為礦柱內平均應力，MPa；Ap為礦柱橫截面積，m2。

而礦柱所承載區域的面積A ＝Ap+Am，其中Am是礦柱所支撐采空區的面積，則礦柱所受的應力σp為：

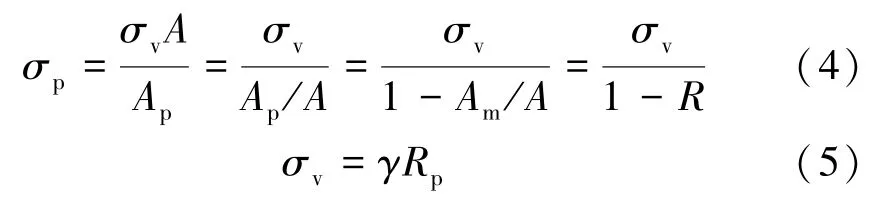
式中R ＝Am/A，定義為面積提取率；Ap＝Wp× Lp；A＝（Wo+Wp） ×（Lp+Wc），Am＝Wo×（Lp+Wc）+Wc×Wp；Wo為礦房寬度；Wp礦柱寬度；σv為礦柱上覆塑性區引起的自重應力。

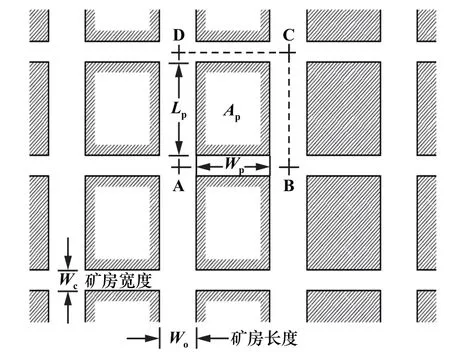
圖2 礦房和礦柱組成的開挖示意圖

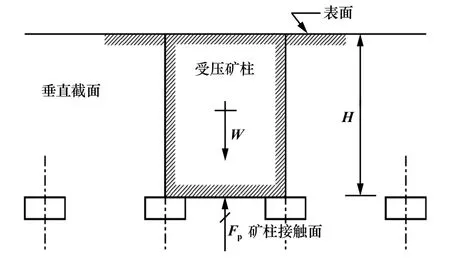
圖3 單個礦柱受力示意圖

因此，礦柱內的應力σp為：

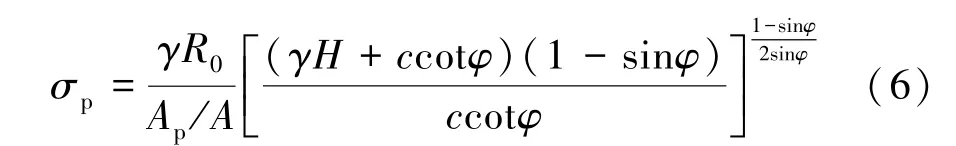
1.1.2 有效區域理論

杜瓦爾首先提出有效區域理論，而后被不斷發展與完善，但其主要用于條帶式開采的礦柱設計中［10］。有效區域理論假定各礦柱支撐上部及與其相鄰的礦柱所平分的采空區上覆巖層的質量。 該方法計算方便、簡單易行，在條形礦柱安全設計方面得到了廣泛應用。

1.1.3 兩區約束理論

兩區約束理論由威爾遜提出并沿用至今，它根據不同的應力狀態，將礦柱受力分為核區和屈服區兩部分，兩端屈服點向里為應力核區（礦柱變形較小），屈服點向外為屈服區（礦柱主要變形區域），并基于實驗數據，確定了屈服區寬度和礦柱承載能力的計算公式［5，11］。 該理論綜合考慮了礦柱的三軸強度特性，更加貼合于工程實際，應用廣泛，但在巖體力學參數取值方面未加以闡述，實際應用過程中仍受到不少限制。

1.1.4 面積承載理論

目前國內設計院應用最為廣泛的是礦柱面積承載理論，即空區內各礦柱所受到的荷載為采空區到地表巖層的自重應力，并假設礦柱支撐面積等于礦柱所分攤的頂板面積與其自身面積的總和［12-13］。 該理論在礦柱荷載計算方面簡單易行，被廣泛應用于工程實踐，其礦柱內平均應力為：

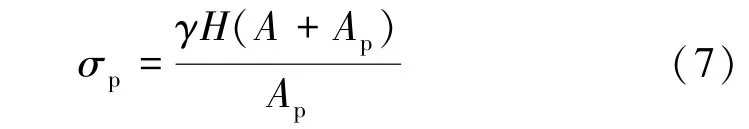
上覆巖柱分攤的開采面積與礦柱布置形式緊密相關，礦山可根據研究內容的需要以及實際情況，選取最為恰當的平均應力計算公式。 在初期對研究區內采空區的礦柱穩定性分析中，可采用正方形礦柱平均應力計算公式來簡化計算，此時礦柱平均應力為：

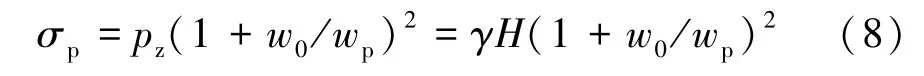
1.2 礦柱強度

100 多年以來，各國學者主要通過室內實驗、現場原位實驗2 種方式對礦柱強度展開研究。 根據實驗結果和現場實際調查，并結合相關理論，得到了多種關于礦柱強度計算的公式。

Bieniawski 對煤柱強度尺寸效應進行了大量實測，認為煤柱強度不是簡單地表現為尺寸越大強度越小，而是存在著一個臨界煤柱尺寸，當礦柱實際尺寸大于臨界尺寸時，煤柱強度將不再隨尺寸增加而減小。 該理論認為煤柱強度與試樣的尺寸之間存在如下關系：

式中Sp為礦柱強度；σc為試樣單軸抗壓強度，MPa；h為礦柱高度，m。

1981 年，Bieniawski 對之前所提出的礦柱強度計算公式進行了修正，修正后的公式為：

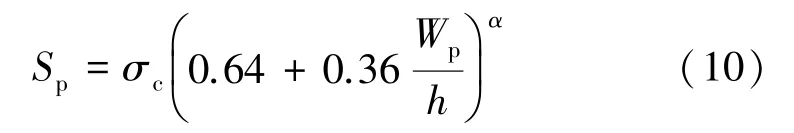
式中α 為常數，主要取決于礦柱寬高比，當其寬高比大于5 時，α 取1.4；否則α 取1.0。

1.3 礦柱安全系數

1.3.1 基于面積承載理論

礦柱安全系數是礦柱強度與礦柱平均應力的比值，根據前文所選取的礦柱強度與平均應力的計算公式，可以得到基于面積承載理論的礦柱安全系數K為：

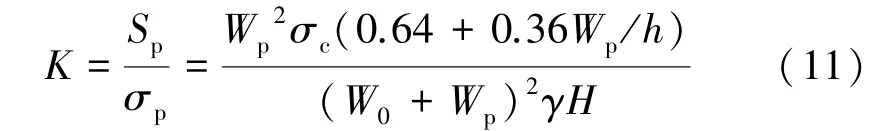
1.3.2 基于普氏理論

基于普氏理論和面積承載理論得到的礦柱應力σp（式（6））和Bieniawski 礦柱強度公式得到的礦柱強度Sp（式（10）），進行理論推導得到礦柱的安全系數為：

對于正方形礦柱，礦柱的安全系數為：

2 工程實例

湖南省某鉛鋅礦經歷了約40 年的以空場法為主的地下開采，形成了數量巨大、范圍廣泛、空區層疊的采空區群。 體量巨大的采空區群時刻威脅著工作人員的生命和財產安全。 據統計，2009～2015 年間，鉛鋅礦區曾發生多起冒頂片幫、透水事故，造成數十名人員傷亡和大量財產損失。

本文以湖南省某鉛鋅礦區群采空區為研究對象，圈定了井下1 365 根礦柱樣本。 對這些礦柱的安全系數進行逐一計算，最終得到了基于面積承載理論及普氏理論的各礦柱安全系數，如表1 所示。 篇幅有限，表2 為鉛鋅礦區Ⅴ礦區第3 采區礦柱安全系數計算結果。

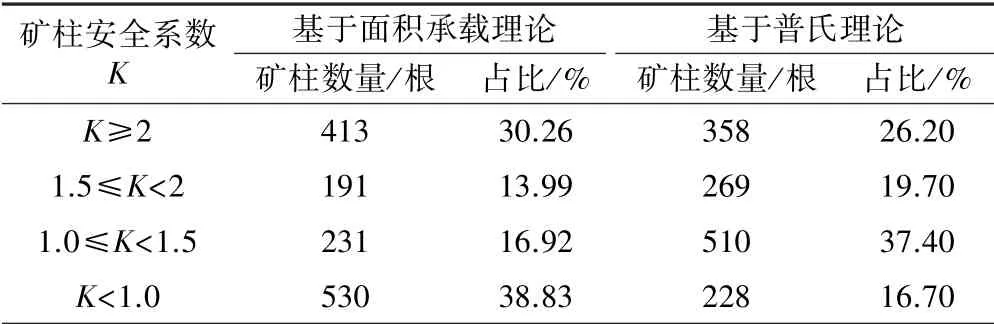
表1 基于面積承載理論及普氏理論的礦柱安全系數分布情況

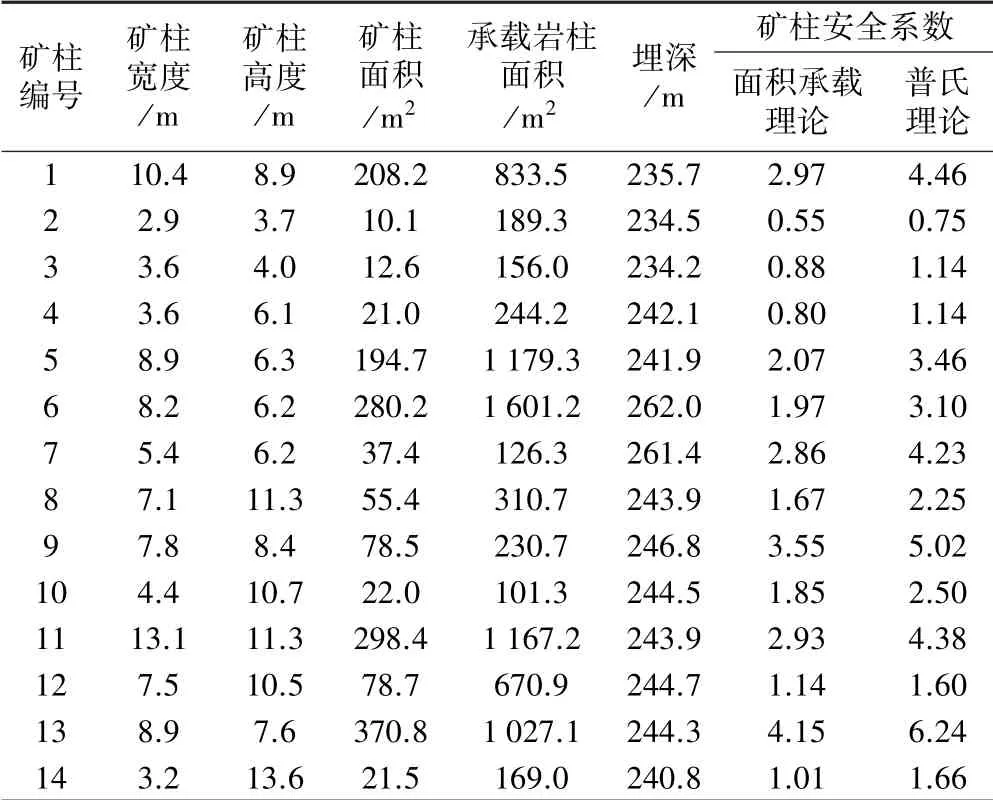
表2 鉛鋅礦區Ⅴ礦區第3 采區礦柱穩定性計算結果

通過以上分析可知，基于面積承載理論的礦柱安全系數有33.83%小于1，處于不穩定狀態。 但據現場實際觀察，這些礦柱仍保持良好的穩定形態，在一定時期內仍能起到對空區的支撐作用，這反證了基于面積承載理論的礦柱安全系數計算方法在該礦區的應用效果不佳，結果過于保守。 同時，與基于普氏理論的礦柱安全系數計算結果也有較大差異。

對比分析，得知該礦區兩種礦柱安全系數計算方法之間的關系可分為3 類：①礦柱埋深50～100 m，兩者數據基本相差不大，該類礦柱約占總數的10%。 ②礦柱埋深100～300 m，兩者結果呈線性相關，該類礦柱約占總數的85%，兩者線性關系為：K普＝1.472 2K面-0.023 1。③礦柱埋深300 m 以上，該類礦柱約占總數的5%，兩者線性關系為：K普＝1.536 9K面-0.006 2。

3 礦柱安全系數三維數值模擬計算與分析

為尋找適合該鉛鋅礦區礦柱安全系數的計算公式，對該礦區1 365 根礦柱安全系數進行計算分析。通過正交試驗可知，影響該鉛鋅礦區礦柱安全系數的關鍵因素主要為礦柱埋藏深度、礦柱橫截面積、礦柱承載巖柱橫截面積、礦柱高度。 為研究采場間距和埋深對礦柱穩定性的影響，通過Midas GTS 和FLAC3D耦合建模的方法，建立了礦柱間距分別為8 m、12 m、16 m、20 m，埋深100～1 000 m，礦柱尺寸均為6 m × 6 m × 8 m。以20 m 間距標準空區模型為例，空區高度8 m，礦柱間距20 m，空區內有9 根礦柱。 根據圣維南原理，所建立的模型尺寸為X ×Y ＝90 m × 490 m，Z方向以空區為界線分為兩部分，上部分高度為埋深高度，下部分高度為200 m，模型的上部直達地表。 將在Midas 中建立好的三維網格模型，利用轉換接口程序轉換到FLAC3D軟件中。 20 m 間距標準空區模型網格如圖4所示。 由于篇幅有限，這里只列出20 m 間距部分標準空區模型及其計算結果，如圖5 所示。

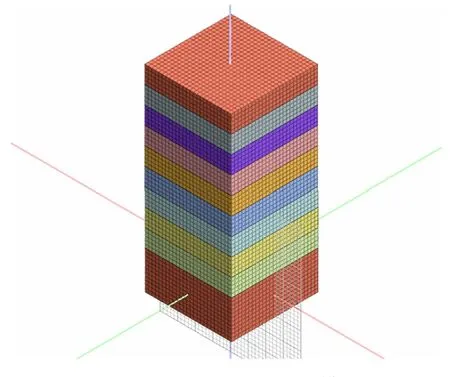
圖4 20 m 間距標準空區模型

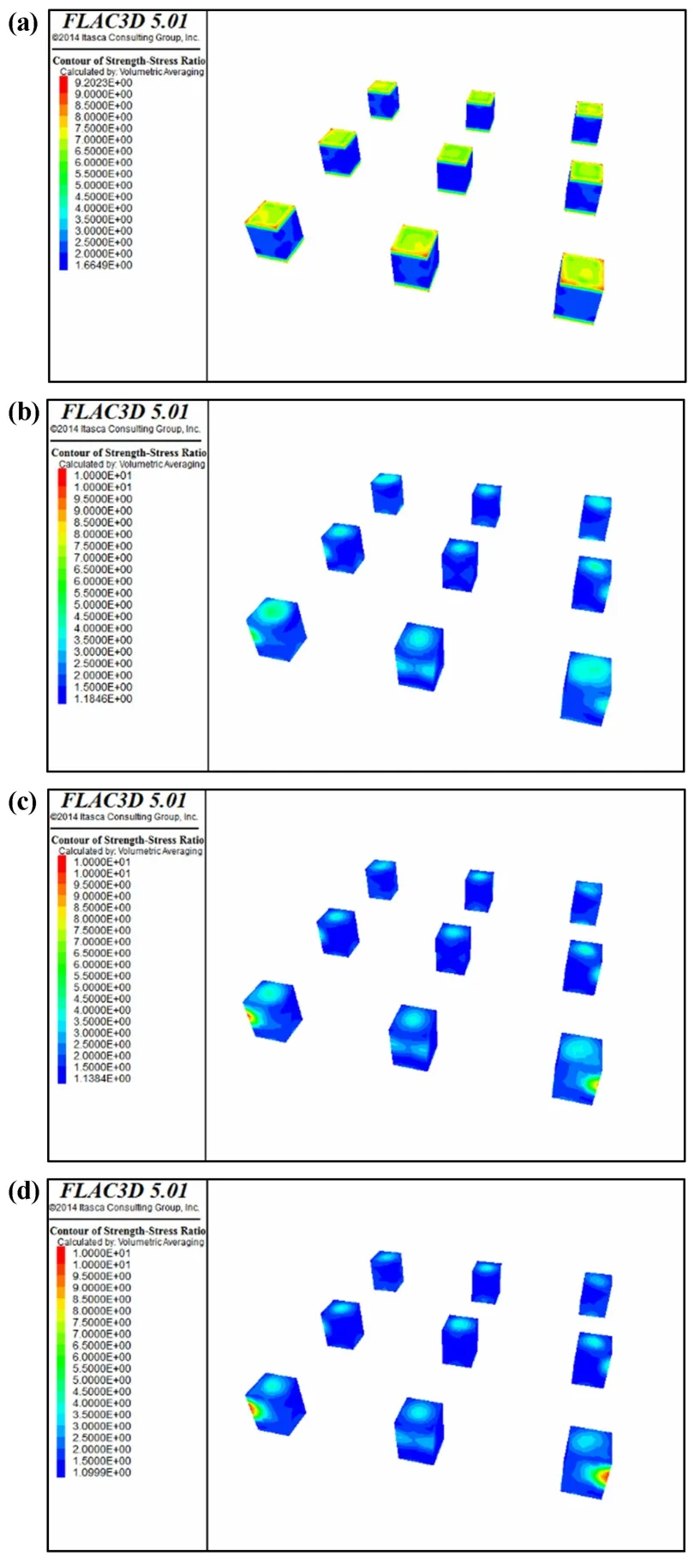
圖5 不同埋深礦柱安全系數云圖

在礦柱穩定的情況下，為了準確分析礦柱應力與礦柱埋深、礦柱間距之間的關系，統計不同間距、不同埋深情況下所有礦柱的安全系數，如表3 所示。

表3 20 m 間距下礦柱安全系數

可以看出在100 m、200 m 和300 m 埋深時，最小安全系數往往出現在礦柱的外表面位置，同時最小安全系數隨著埋深增加而逐漸減小且都大于1，表明礦柱穩定性良好。 隨著埋深增加，最小安全系數出現在礦柱的四周和頂部位置，表明隨著上覆巖層重力增加，礦柱頂部所受壓力增加，其安全系數也會相應減小。

4 礦柱安全系數優化研究

為了深入分析礦柱應力與礦柱埋深、礦柱間距之間的關系，通過Matlab 軟件對所有的礦柱安全系數進行二元多項式擬合（如圖6 所示），可得到礦柱應力與礦柱埋深、礦柱間距之間的函數關系式。 本文在進行礦柱穩定性分析時，均選用Bieniawski 礦柱強度公式，因此基于擬合出的函數關系，可推導出礦柱應力計算公式為：

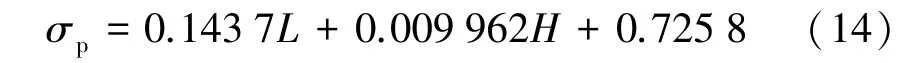
式中σp為礦柱應力，MPa；L為礦柱間距，m；H為礦柱埋深，m。

圖6 二元多項式擬合曲面圖

基于Bieniawski 礦柱強度公式，可得出適合該礦區的礦柱安全系數計算公式為：

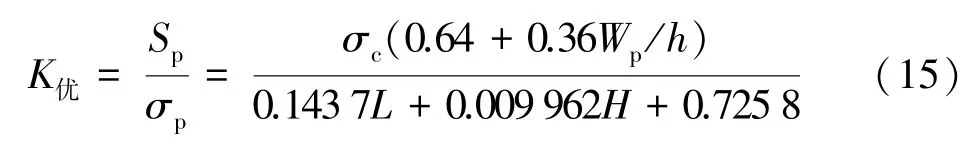
5 結 語

1） 基于面積承載理論對礦柱所受荷載進行了詳細分析，推導出基于面積承載理論的礦柱安全系數的計算公式。 基于普氏理論推導了礦柱實際承載上覆巖層的厚度，通過力學平衡分析推導了單個礦柱內荷載的計算公式，最終推導出基于普氏理論的礦柱安全系數的計算公式。

2） 基于面積承載理論和普氏理論計算了采空區內1 365 根礦柱的安全系數，結果表明基于面積承載理論的礦柱安全系數計算公式過于保守，與現場實際不符。 對比分析可知，對于鉛鋅礦區埋深100 ～300 m的礦柱（占比85%），2 種理論計算的礦柱安全系數之間存在著線性相關性。

3） 通過Midas GTS 和FLAC3D耦合建模的方法，以鉛鋅礦區Ⅴ礦區3 采區為例，構建了不同礦柱間距與礦柱埋深的標準空區模型，研究礦柱應力與礦柱間距、礦柱埋深之間的關系，并通過Matlab 軟件進行二元多項式擬合，最終得到了優化后的礦柱安全系數計算公式。

4） 本文僅對礦柱上覆荷載進行了優化研究，未對礦柱強度公式作進一步討論，有待下一步細化研究。