基于合數階雙線性對的可搜索加密方案分析與改進

鄧志輝,王少輝,王 平

(1.南京郵電大學 計算機學院,南京 210003; 2.江蘇省無線傳感網高技術研究重點實驗室,南京 210003)

0 概述

隨著互聯網技術的迅速發展,人們在日常工作和生活中產生及使用的數據量不斷增大,數據規模已由PB級發展到EB級甚至ZB級,如何存儲和處理大規模數據成為亟待解決的問題。云計算是通過互聯網提供動態、易擴展和虛擬化資源的計算方式,而云存儲是云計算的應用模式,其可遠程高效存儲數據,能節省大量存儲空間,因此引起了人們的廣泛關注,并成為存儲大數據的有效手段。

在云存儲應用初期,部分用戶以明文形式上傳數據,由于云存儲具有開放性和分布性,數據脫離用戶的物理控制存儲在云端后,一旦被外部攻擊者截獲或被惡意云服務提供者泄露,將無法挽回損失。因此,為保證所傳數據的隱私性和安全性,用戶會將數據加密后再上傳到云端。加密存儲數據在一定程度上可以保證數據的隱私與安全,但卻給數據檢索帶來困難。

由于基于明文關鍵字的傳統檢索模型無法在密文下進行檢索,因此2000年SONG等人[1]在對稱密碼體制的基礎上提出可搜索加密的概念,并設計出可在密文下進行檢索的SWP方案。2004年BONEH等人[2]首次提出公鑰關鍵字搜索加密(Public Key Encryption with Keyword Search,PEKS),并設計一種應用于郵件路由分發場景的方案,將不同郵件分發到不同設備中,公鑰關鍵字搜索加密允許服務器根據接收到的陷門對不同關鍵字郵件選擇分發路由,且不會泄露郵件內容,但是該方案在安全和效率方面存在不足。WATERS等人[3]隨后提出用來構造可搜索加密審計日志的新PEKS方法。GOLLE等人[4]也提出基于連接關鍵詞的可搜索加密方案,可實現對多個關鍵詞的搜索功能。2006年BYUN等人[5]分析了文獻[2]中PEKS方案,指出該方案容易遭受關鍵字猜測攻擊[6-7],此后研究者們提出大量抗關鍵字猜測攻擊的PEKS方案[8-10]。2016年XU等人[11]提出合數階雙線性群下的PEKS方案,該方案系統參數比其他方案更少,且其安全性是基于靜態假設下合數階子群的不可區分性。文獻[12]提出雙服務器模型,通過2個獨立服務器分享秘密檢索陷門執行搜索算法抵抗關鍵字猜測攻擊。文獻[13]通過加入發送者公私鑰生成可搜索密文和陷門,使服務器無法自行生成關鍵詞陷門測試密文。文獻[14]提出一種通過采用非確定算法生成關鍵字密文和陷門的方案,可高效抵抗關鍵字猜測攻擊。

然而PEKS框架本身存在一定不足,即多數PEKS方案都需在服務器與接收者之間建立安全信道以傳送陷門,否則外部攻擊者很容易截獲關鍵字陷門進行搜索操作,進而得到加密數據信息,但是建立安全信道代價太高且很難實現。為解決該問題,文獻[15]提出無安全信道的公鑰關鍵字搜索加密(Secure-Channel Free Public Key Encryption with Keyword Search,SCF-PEKS)方案,由于關鍵字密文的生成需要云服務器公鑰參與,因此只有云服務器能夠使用自身私鑰檢查關鍵字密文和陷門是否包含相同關鍵字。通過該方式,用戶可在無安全信道的情況下將關鍵字陷門發送到數據存儲服務器。但是上述方案依賴于隨機oracle模型,而隨機oracle模型不能真正反映方案在現實世界中的安全性。2009年FANG等人[16]提出首個在標準模型下安全的SCF-PEKS方案,但該方案檢測算法太復雜,不具備高效性。2011年EMURA等人[17]利用匿名IBE、標簽加密方案和一次性簽名提出SCF-PEKS方案的通用設計方法。近期LI等人[18]從靜態假設出發提出在標準模型下安全高效的SCF-PEKS方案,該方案主要基于判定性子群假設和DBDH假設,與現有在標準模型下構造的相關方案相比,具有更簡潔的結構。

2009年RHEE等人[19]指出SCF-PEKS方案不能抵抗由外部攻擊者發起的離線關鍵字猜測攻擊,并在文獻[20]中引入陷門不可區分性的概念,證明抵抗關鍵詞猜測攻擊的充分條件是陷門的不可區分性。本文對文獻[11,18]提出的基于合數階雙線性對的可搜索加密方案進行分析,發現上述方案的關鍵字陷門生成算法無法滿足搜索關鍵字陷門的不可區分性。針對該問題,本文在文獻[11,18]方案的基礎上,提出一種改進的無安全信道公鑰可搜索加密方案,同時基于DBDH假設對其是否滿足關鍵字陷門的不可區分性進行證明,并研究了該方案的計算復雜度和空間存儲復雜度。

1 基本知識

1.1 合數階雙線性群

定義1(合數階雙線性映射) 設G和GT是2個階為N=p1p2p3的乘法循環群,g是G的生成元。雙線性映射e:G×G→GT滿足以下性質:

1)可計算性:映射e:G×G→GT可以被有效計算。

3)非退化性:e(g,g)≠1。

e(h1,h2)=e(gp2p3α1,gp1p3α2)=e(gα1,gp3α2)p1p2p3=1

(1)

如果選取i≤j、hi∈Gpi、hj∈Gpj,則e(hi,hj)是群GT中的單位元,這說明合數階雙線性群中各子群Gp1、Gp2和Gp3相互正交。

1.2 判定性子群假設

假設1給定群生成器G(λ),定義其分布如下:

(2)

Pr[A(D,T1)=1]|關于λ是可忽略的。

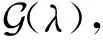
(3)

1.3 DBDH假設

1.4 PEKS和SCF-PEKS

PEKS和SCF-PEKS方案都涉及發送者(數據擁有者)、接收者(用戶)和云服務器三方參與者。發送者生成關鍵字的可搜索密文并將其連同密文數據發送給云服務器,接收者生成關鍵字陷門,云服務器根據關鍵字密文和陷門執行數據檢索操作,并將匹配的密文數據發送給接收者。

1.4.1 PEKS方案

定義2公鑰可搜索加密方案由以下4個算法組成:

1)Setup(λ)算法。輸入安全參數λ,算法生成全局參數gp,用戶公鑰pk和私鑰sk。

2)PEKS(gp,pk,ω)算法。由發送者執行,輸入全局參數gp、用戶公鑰pk和關鍵字ω,輸出關于關鍵字ω的可搜索密文C。

3)Trapdoor(gp,sk,ω)算法。由用戶執行,輸入全局參數gp、用戶私鑰sk和關鍵字ω,生成關鍵字陷門Tω。

4)Test(gp,C,Tω)算法。輸入全局參數gp、可搜索密文C和關鍵字陷門Tω,服務器對關鍵字密文和陷門進行驗證,如果驗證匹配則輸出1,否則輸出0。

1.4.2 SCF-PEKS方案

SCF-PEKS方案與PEKS方案主要區別在于云服務器的公鑰和私鑰是否分別參與了可搜索密文生成算法和檢測匹配算法。由于PEKS方案沒有使用云服務器的公私鑰對,因此其傳送關鍵字陷門時需要使用安全信道才能避免受到攻擊。而因為SCF-PEKS方案中云服務器的公鑰參與了可搜索關鍵字密文生成過程,只有擁有對應私鑰的云服務器才能進行檢測匹配算法,所以傳送關鍵字陷門時不需安全信道參與。

定義3無安全信道的公鑰可搜索加密方案由以下4個算法組成:

1)Setup(λ)算法。輸入安全參數λ,生成全局參數gp,并輸出云服務器的公私鑰對(pkS,skS),以及接收者的公私鑰對(pkR,skR)。

2)SCF-PEKS(gp,pkS,pkR,ω)算法。輸入gp、接收者的公鑰pkR、云服務器的公鑰pkS以及關鍵字ω,由發送者輸出關鍵字ω的可搜索密文C。

3)Trapdoor(gp,skR,ω)算法。輸入gp和接收者的私鑰skR,由接收者輸出關鍵字ω的陷門Tω。

4)Test(gp,skS,C,Tω)算法。輸入gp、關鍵字密文C和關鍵字陷門Tω,云服務器利用自身私鑰對密文和陷門進行匹配驗證,如果匹配則輸出1,否則輸出0。

1.5 陷門不可區分性

為避免關鍵字猜測攻擊,在設計方案時要保證關鍵字密文和陷門的不可區分性。本節只給出陷門不可區分性的安全性定義,其他可參考文獻[18]。根據文獻[20]提出的陷門不可區分性概念及安全模型,假設敵手A為外部攻擊者(不是服務器和接收者),關鍵字陷門的不可區分性通過多項式時間的挑戰者B與敵手A之間交互游戲來描述,具體過程如下:

1)Setup。給定安全參數λ,挑戰者B生成全局參數gp、云服務器和接收者的公私鑰對(pkS,skS)和(pkR,skR),并將gp、pkR和pkS發送給敵手A。

2)Queryphase1。敵手A可適應性的詢問如下預言機OT,訪問次數以多項式時間限定:

(1)搜索陷門預言機OT。輸入接收者的私鑰skR和選擇的關鍵字ω∈KSω,OT預言機返回關鍵字陷門Tω←Trapdoor(gp,skR,ω)給敵手A。

(2)Challenge。一旦敵手A決定Queryphase1結束,A選擇未詢問過OT預言機的關鍵字(ω0,ω1),并將其發送給挑戰者B。挑戰者B隨機選擇b∈{0,1},計算關鍵字ωb對應的陷門Tωb←Trapdoor(gp,skR,ωb)并返回給敵手A。

3)Queryphase2。敵手A可以繼續訪問OT預言機,但要求不能就關鍵字(ω0,ω1)對預言機OT進行詢問。

4)Guess。敵手A猜測b′,如果b′=b,則敵手A獲勝,否則敵手A失敗。

2 可搜索加密方案分析

本節主要對文獻[11,18]分別提出的2個基于合數階雙線性對的公鑰可搜索加密方案進行分析。上述方案對關鍵字陷門的設計均無法保證關鍵字陷門不可區分性,存在安全問題。

2.1 文獻[11]方案分析

文獻[11]方案的安全性主要基于合數階雙線性群的子群不可區分性,該方案具有IND-CKA安全性,方案具體設計可參考文獻[11],下文對其中的Setup算法和Trapdoor算法進行闡述。

對文獻[11]方案的安全性分析如下:

假設存在1個外部攻擊者A,給定2個關鍵字(ω0,ω1),且A可獲取包含目標關鍵字ωb∈{ω0,ω1}的陷門Tωb=[T1,T2]=[gα(uωbh)rR3′,grR3],外部攻擊者A可通過以下攻擊方式來區分該陷門中的關鍵字:

1)外部攻擊者A通過系統參數gp={G,GT,e,N,u,g,h,e(g,g)α}獲取u、g、h的值。

2)A隨機選擇ω′∈{ω0,ω1},并計算得到:

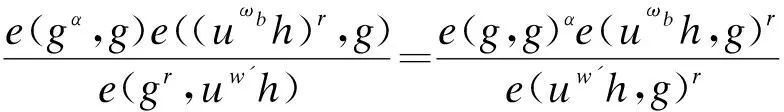
(4)

3)若ωb=ω′,則M=e(g,g)α,由于e(g,g)α已知,外部攻擊者A可不通過驗證測試算法就能區分并獲取陷門中的關鍵字,因此該方案不滿足陷門的不可區分性。

2.2 文獻[18]方案分析

文獻[18]提出在標準模型下利用合數階雙線性對的SCF-PEKS方案,該方案具有安全性和高效性,且主要基于判定性子群假設和DBDH假設,方案具體設計可參考文獻[18],以下對其中的Setup算法、SCF-PEKS算法和Trapdoor算法進行闡述。

3)Trapdoor(gp,skR,ω)算法。接收者確認關鍵字后,隨機選取R3∈Gp3,計算Tω=u1/(y+ω)R3,返回Tω。

對文獻[18]方案的安全性分析如下:

由于該方案在無安全信道的環境下傳送關鍵字陷門,因此陷門很容易被攻擊者獲取,且攻擊者只需按如下攻擊方式進行計算,便可輕易區分并獲取陷門中的關鍵字,具體攻擊過程為:

1)給定2個關鍵字(ω0,ω1),假設存在1個外部攻擊者A,將包含目標關鍵字ωb∈{ω0,ω1}的陷門Tωb=u1/(y+ωb)R3發送給A。

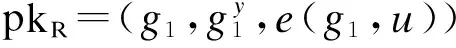
3)A隨機選擇ω′∈{ω0,ω1},并計算得到:

(5)

4)若ωb=ω′,則M=e(u,g1),由于e(u,g1)在pkR中已知,攻擊者A可區分陷門中的關鍵字,因此該方案不滿足陷門的不可區分性。

3 SCF-PEKS改進方案

針對文獻[11]和文獻[18]方案存在的安全問題,本文提出一種改進的基于合數階雙線性對的無安全信道可搜索公鑰加密方案,該方案可保證關鍵字陷門的不可區分性,且能抵抗外部關鍵字猜測攻擊。

3.1 本文方案設計

本文方案由4個算法組成,其中Setup(λ)算法、SCF-PEKS(gp,pkS,pkR,ω)算法與文獻[18]方案中算法一致,另外改進的2個算法具體如下:

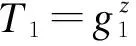
2)Test(gp,Tω,C,skS,ω)算法。服務器先使用自身私鑰計算t=H(e(U,h)x)和n=H(e(T1,h)x),再檢驗e(Vt,T2)=Wn是否成立。若等式成立,則輸出1,否則輸出0。

對本文方案的正確性證明如下:

(6)

(7)

(8)

由式(6)～式(7)可知,服務器通過自身私鑰可計算出正確的t和n,將其代入式(8)計算得知,陷門和可搜索密文能夠正確匹配,從而證明了本文方案具有正確性。

本文方案主要在生成陷門的Trapdoor算法基礎上進行重新設計。根據上述分析,改進方案在生成陷門時增加1個n次冪,其中n=H(e(X,h)z),z為隨機值。從而保證陷門即使在被攻擊者獲取的情況下,也無法通過計算區分出關鍵字,且必須計算出n值才能進行驗證操作,雖然增加了計算量,但是可保證關鍵字陷門的不可區分性。采用對文獻[18]方案相同的攻擊方式對本文方案進行攻擊,可以得到:

(9)

若ω′=ωb,則M=e(u,g1)n,此時對于外部攻擊者而言,雖然e(u,g1)已知,但n值需要通過云服務器或接收者的私鑰計算得到,攻擊者無法通過M值判斷ω′是否等于ωb,不能對陷門中的關鍵字進行區分,因此,本文方案能抵抗外部關鍵字猜測攻擊。

3.2 安全性證明

本文主要證明改進方案關鍵字陷門的不可區分性,而由于可搜索密文的不可區分性等其他安全性基于判定性子群假設和DBDH假設,因此本文安全性證明過程與文獻[18]中的安全性證明過程基本一致,具體可參考文獻[18]。

定理1如果DBDH假設是困難的,那么對于任意概率多項式時間算法的敵手A,能區分關鍵字陷門的概率優勢可忽略。

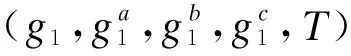
敵手A和挑戰者B進行游戲如下:

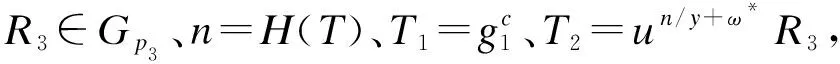
4)Guess。敵手A輸出猜測b′。在驗證過程中,當b′=b時,n=H(e(T1,h)a)=H(e(g1,g1)abc),T=e(g1,g1)abc,則Tω*為合法輸出,返回1;當b′≠b時,T≠e(g1,g1)abc,則T是GT中隨機元素,返回0。

如果敵手A能區分陷門中的關鍵字,那么挑戰者B便可攻破DBDH假設。因此,本文方案的關鍵字陷門具有不可區分性,可抵抗外部攻擊者的關鍵字猜測攻擊。

3.3 性能比較

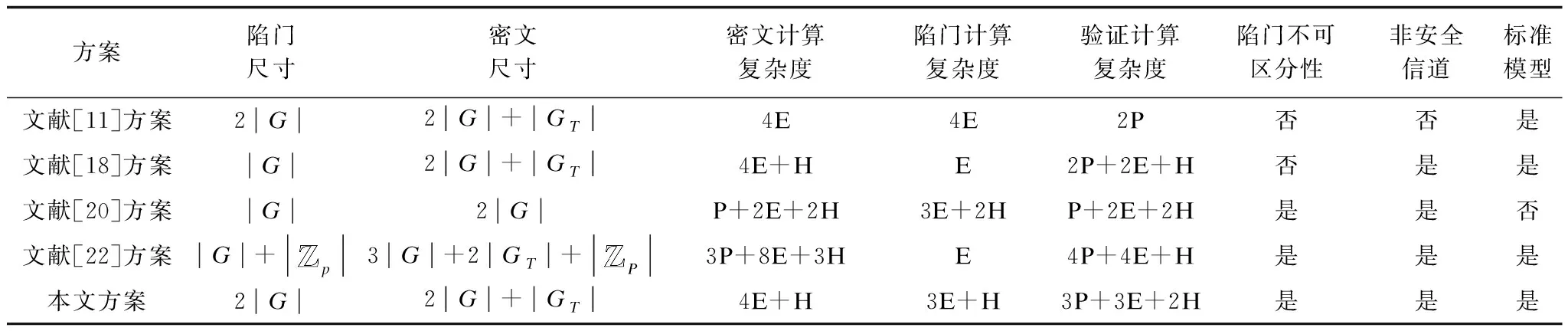
表1 本文方案與其他方案的性能對比

4 結束語

本文對傳統基于合數階雙線性對的可搜索公鑰加密方案進行研究,指出其中陷門算法不具有關鍵字不可區分的安全屬性,并提出一種改進的基于合數階雙線性對的可搜索加密方案。該方案在陷門、密文尺寸及計算復雜度與原方案接近的情況下,可保證關鍵字陷門的不可區分性,從而抵抗外部關鍵字猜測攻擊。關鍵字猜測攻擊較多由外部攻擊者發起,如果由內部攻擊者(惡意服務器)發起猜測攻擊,則更容易造成數據泄露。后續將在本文對外部關鍵字猜測攻擊研究的基礎上,繼續對合數階雙線性對進行改進,以抵抗內部關鍵字猜測攻擊并提高計算效率。