基于結構化的小學數學教學策略
江蘇連云港市東海縣牛山小學 黃春雷
在新課改時代背景下,小學生數學核心素養的培養已經成為數學教學的價值取向。最新的教育研究指出,核心素養是一種結構化的學習能力。對于教師而言,教給學生數學知識的關鍵,不是教給學生多少的問題,而是怎么教的問題,也就是教學結構化的問題。在小學數學教學中,結構化教學以完善和發展學生數學認知結構為目的,幫助學生真正融通和建構數學知識,并充分感受和把握知識結構和方法結構,形成完善的思維結構,促進學生的知識、策略、思維的系統化和結構化,為培養學生的核心素養提供強有力的支撐。那么如何實施結構化教學呢?筆者認為,結構化教學要從三個方面進行實踐和落實,一是讓學生掌握數學雙基,二是讓學生掌握典型例題,三是培養學生數學思想方法。通過這樣層次分明的結構化教學,讓學生領會數學的本質,發展數學思維。
一、串聯知識網絡,培養整體觀念
在小學數學教學中,很多數學知識都起著承上啟下的重要作用,它既是課堂教學某一個階段的終點,但同時又是另一個階段的起點。知識之間層層關聯,形成系統化的知識網絡。因此,教師要串聯知識網絡,幫助學生梳理小知識與大知識之間的關系,從整體的高度去全面把握數學結構,培養學生的數學整體觀念。
比如,在教學“三角形單元復習”這一內容時,根據學情,筆者發現學生對這一單元的知識順序并沒有一個整體的把握和聯系,所學的知識比較零散,無法系統建構知識結構。為此,筆者帶領學生對所學內容展開了梳理,要求學生將有關聯的知識進行歸類。學生通過討論交流后,將三角形的相關知識根據知識點歸類,以此形成了相關三角形的知識結構:三角形有兩個分支,一個是邊,一個是角。在邊的分支中,可以按照位置關系和長短進行分類,在角的分支中,既可以按照角的大小進行分類,又可以借此研究三角形的內角和。與此同時,學生通過梳理知識結構,深刻理解和把握三角形的關鍵要素:三角形的邊和角的特點決定著三角形的穩定性。筆者讓學生根據自己的分類,形成一個思維導圖(如圖1)。
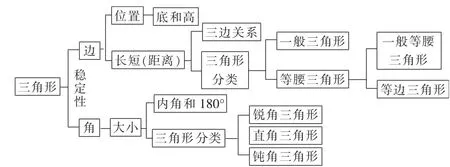
圖1
通過這樣結構化的圖示,學生將所學的整個單元的知識串聯起來,形成一個知識網絡,不但有利于對數學整體概念的理解和記憶,也能夠幫助學生拓展后續的關于圖形與幾何的知識學習,構建數學整體觀念。
二、重視基本技能,發展動手能力
在小學數學課堂教學中,基本的數學技能是執行和支撐數學學習的關鍵環節。只有讓學生扎實掌握了數學基本技能,才能夠將數學知識內化于心,在實踐生活中活學活用。因此,教師不僅要重視數學技能的培養,還要重視基本技能的結構化教學,既授之以“魚”,又授之以“漁”,讓數學技能以結構化、體系化為動力生長起來,整體發展學生的動手能力。比如,在教學“三角形的高”這一內容時,學生存在的一個學習難點在于:無法理解直角三角形的直角邊是高;也無法理解鈍角三角形的高在三角形外。究其原因在于,學生不能將高和垂線段建立關聯。為了讓學生突破三角形的高的畫法這一難點,筆者將畫高和畫垂線段的技能進行關聯,幫助學生建立畫高的結構化技能。筆者先讓學生復習一下學過的畫垂線段的技能,學生經過操作,再次深刻確認垂線段就是“過一點作已知直線的垂線”,接著筆者讓學生確定三角形中高的定義,借此引導學生將高和垂線段建立關聯,學生由此有了正向遷移,認識到高和垂線段一樣,都是從一點作已知直線的垂線。那么,在三角形中,畫高就是從頂點作底邊的垂線段。由此,學生通過操作,深刻理解了高與垂線段的關聯,就能夠運用已經學過的畫垂線段的技能解決新的畫高的問題,這時候畫高不再是一個獨立的新問題和新技能,而是原有的畫垂線段的技能的延伸和拓展。通過以上環節的結構化教學,學生將畫垂線段和畫高建立了結構化的關聯,形成了更大的技能體系,從而學會理性變通,系統化運用已有的技能解決面臨的新問題,習得新技能,發展動手能力。
三、注重策略引導,培養探究精神
在小學數學課堂教學中,教師要注重結構化策略引導,在尊重學生認知規律的基礎上,帶領學生進行結構化體驗、感受,進而探究、推理,一步步尋找方法,實現對數學概念的深刻理解,并讓策略教學成為常態模式。
比如,在教學“三角形三邊關系”這一內容時,筆者先讓學生自主猜想,并將自己猜想的三角形的三邊關系進行自主驗證,驗證的過程是學生集體討論、集體操作、集體推理的過程。學生通過自主探究,對三角形的三邊關系建立了一個結構化的研究策略,在面對同樣的問題時也可以積累相應的方法進行研究。在學習“三角形的內角和”時,學生從自己在不同的地方得到的結論出發,展開驗證。驗證的過程是一個用量、拼、折、畫進行操作的過程,通過操作最終得到結論。對于學生來說,這樣的教學引導,就是一個構建策略模型的結構化歷程,學生能夠由此形成探究策略的結構化,在探究中找到科學的探究方法,并在此過程中發展探究精神,建立科學的數學觀。
四、滲透數學思想,提升數學思維
對于數學教學來說,思維是學習的靈魂。沒有數學思維,數學活動就是毫無價值的空洞的行為。因此,在小學數學課堂教學中,教師要滲透數學思想方法,尤其是培養學生具有結構化的數學思維,不但能夠理性、科學地看待數學問題,而且能夠學會運用數學思維進行創造,順利解決數學問題。
比如,在教學蘇教版數學“三角形的三邊關系”這一內容時,學生有一個認知上的難點,即兩點之間線段最短。這個難點也是學生學習三角形三邊關系的關鍵點。為此,筆者先從學生的直觀感知入手,出示A、B兩地之間的4條路線(如圖2),讓學生思考:想要更快到達B地,你選擇哪條路?學生根據日常經驗,自然而然地選擇第三條。筆者追問學生:為什么?說說你的理由。學生根據將毛線拉直的生活經驗,認為彎曲的線段(如第二條線)會比拉直的線段更長。在這四條線段中,第三條相比而言,拉得更直。透過這樣直觀的感知,學生逐漸領悟到化曲為直的轉化思想。有了這個直觀的數學思想方法,學生就可以展開有根據、有結構的數學思維和數學判斷,得到直觀認知:兩點之間線段最短。
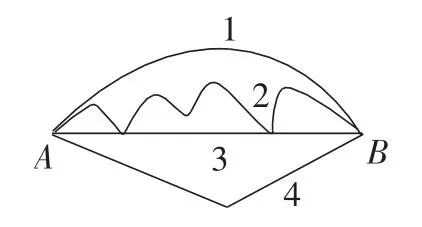
圖2
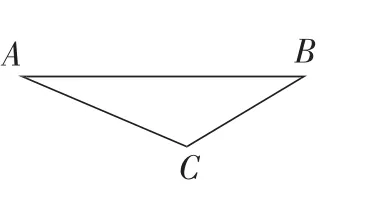
圖3
緊接著,筆者引導學生驗證三角形三邊關系的結論。學生在進行結論推理之后,筆者將問題再次引入兩點之間距離最短的問題上(如圖3),讓學生證明三角形兩邊之和大于第三邊。
經過例證環節后,學生再一次感受轉化思想的價值和意義。教師在數學思想方法的滲透過程中,不僅幫助學生學會了理性思維,而且培養了思維的整體化和結構化,大大提升了學生的數學思維能力。
總之,在小學數學課堂教學中,教師要注重引導學生從知識、技能、策略、思維四個方面進行結構化建構,全面理解和學習數學知識,踐行數學理論,尋找有效的問題解決策略,由此培養數學核心素養。

