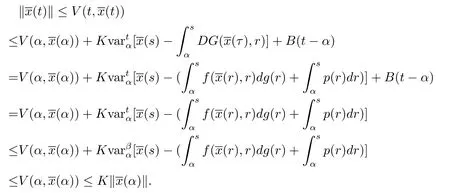測度微分方程的Lipschitz穩定性
李寶麟,席 婭
(西北師范大學數學與統計學院,甘肅 蘭州 730070)
1 引言
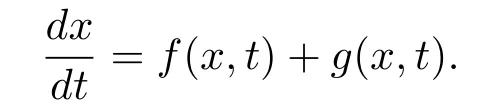
如果擾動項g(x,t)是連續可積的,那么受擾動之后的系統仍舊是常微分方程,它的解仍舊是連續的,如果擾動項是脈沖型的,那么擾動之后系統的狀態就不會隨著時間連續變化而變化,而是呈現出一種瞬時狀態.為了研究這類問題,我們對上述方程加上一種脈沖型的擾動,這就給出如下形式的方程

其中Dx和Du分別表示函數x和u的分布導數.形如(1.1)的方程叫做測度微分方程.由于測度微分方程的解沒有連續性,又沒有隨機系統那么復雜,因此,我們可以說測度微分方程是一種不同于經典不連續系統的新的不連續系統.測度微分方程已經被很多學者研究(見文獻[1–4]).
在文[5]中Dannan和Elaydi研究了常微分方程的Lipschitz穩定性;文[6]中作者討論了一類脈沖微分系統的Lipschitz穩定性;文[7]中作者給出了脈沖泛函微分方程的Lipschitz穩定性;文[8]中作者建立了廣義常微分方程的變差一致Lipschitz穩定性,一致Lipschitz穩定性和一致整體Lipschitz穩定性,并通過滯后型脈沖微分方程在一定條件下與廣義常微分方程的等價關系,討論了滯后型脈沖微分方程的Lipschitz穩定性.本文是在文[8]的基礎上,通過測度微分方程與廣義常微分方程的等價關系,定義了測度微分方程

和擾動后的測度微分方程

的變差一致Lipschitz穩定性,一致Lipschitz穩定性和一致整體Lipschitz穩定性,并建立了測度微分方程和擾動后的測度微分方程的Lipschitz穩定性定理.方程(1.2)和方程(1.3)的等價方程為
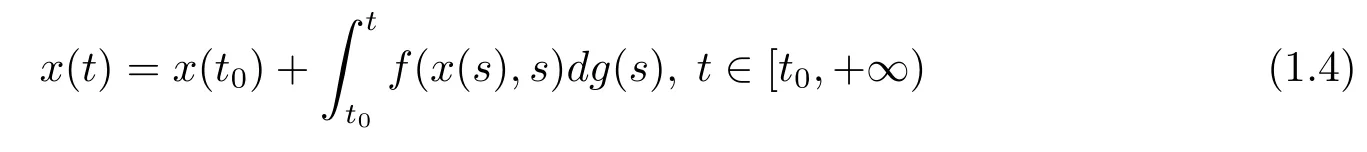
和
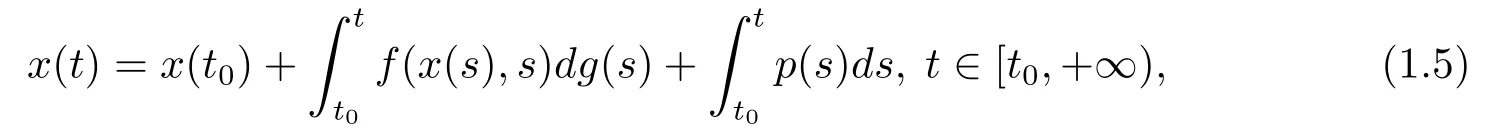
其中f:Bc×[t0,+∞)→Rn,Bc={y∈Rn,‖y‖<c},g:[t0,+∞)→R,p:[t0,+∞)→Rn是比Lebesgue-Stieltjes可積更廣泛的Kurzweil-Henstock-Stieltjes可積函數和Kurzweil-Henstock可積函數(見文[10]).
函數x:[a,b]→Rn為[a,b]上的正則函數是指若函數x的左右極限
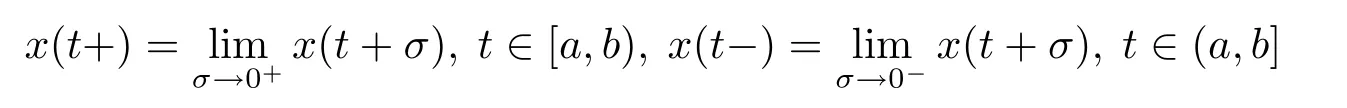
分別存在且有限(正則函數在有限區間上有界,在無窮區間上不一定有界).記G*([a,b],Rn),[a,b]?[t0,+∞)是定義在[a,b]上的正則函數全體,并且是左連續的.G*([t0,+∞),Rn)為關于函數x:[t0,+∞)→Rn的一個向量空間,使得對所有[a,b]?[t0,+∞),x|[a,b]屬于空間是關于所有x∈G*([t0,+∞),Rn)的一個向量空間,使得
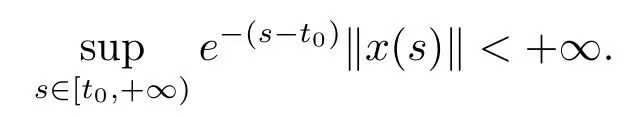
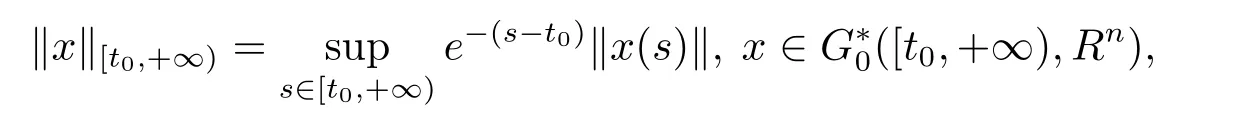
記Ω=Bc×[t0,+∞),本文假定函數f:Ω→Rn,g:[t0,+∞)→R,p:[t0,+∞)→Rn滿足下列條件
(H1)函數g:[t0,+∞)→R在[t0,+∞)上是不減的左連續函數.
(H2)對每一個x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),Kurzweil-Henstock-Stieltjes積分存在.
(H3)存在一個關于g的局部Kurzweil-Henstock-Stieltjes可積函數M:[t0,+∞)→R+,使得對任意的x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),s1<s2,
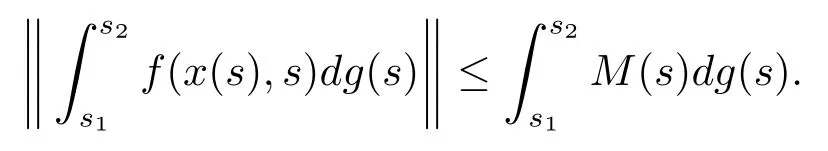
(H4)存在一個關于g的局部Kurzweil-Henstock-Stieltjes可積函數L:[t0,+∞)→R+,使得對任意的x,,s1,s2∈[t0,+∞),s1<s2,
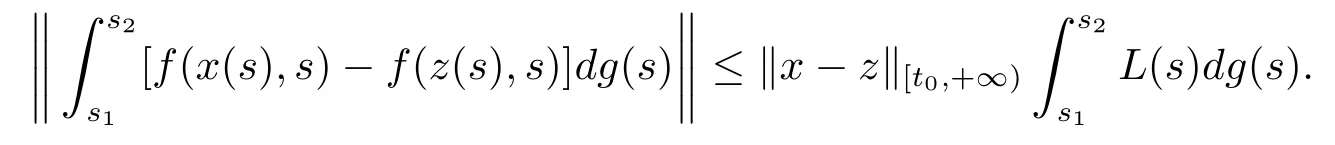
(H5)對每一個x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),Kurzweil-Henstock積分存在.
(H6)存在一個局部Kurzweil-Henstock可積函數N:[t0,+∞)→R+,使得對任意的x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),s1<s2,
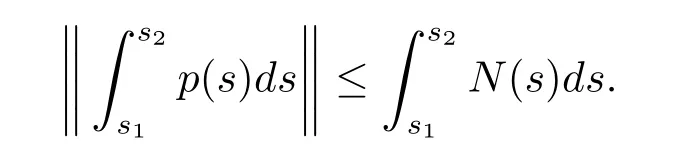
本文主要分為三個部分.第二部分給出了本文所需要的一些定義和引理,第三部分定義了測度微分方程和擾動后的測度微分方程的變差一致Lipschitz穩定性,一致Lipschitz穩定性和一致整體Lipschitz穩定性,并建立了測度微分方程和擾動后的測度微分方程的Lipschitz穩定性定理.
2 預備知識
本節介紹了廣義常微分方程的相關定義和引理及測度微分方程與廣義常微分方程的等價關系.
定義2.1[9]稱函數U:[a,b]×[a,b]→Rn在區間[a,b]上Kurzweil可積,如果存在I∈Rn,使得對任意的ε>0,存在正值函數δ:[a,b]→(0,+∞),使得對[a,b]上的任何δ(τ)-精細分劃D={(τj,[αj-1,αj]),j=1,2,···,k},其中τj∈[αj-1,αj]?[τj-δ(τj),τj+δ(τj)],有

稱I為U在[a,b]上的Kurzweil積分,記作特別地,當U(τ,t)=f(τ)g(t)時,
定義2.2[9]設函數F:Ω→Rn,如果對所有的t∈[α,β],(x(t),t)∈Ω,且對任意的s1,s2∈[α,β],有等式成立,則稱x:[α,β]→Rn是廣義常微分方程

在區間 [α,β]?[t0,+∞)上的解.
定義2.3[9]設不減函數h:[t0,+∞)→R,函數F:Ω→Rn屬于函數族F(Ω,h),是指F滿足以下條件:對任意的(x,s1),(x,s2)∈Ω,有
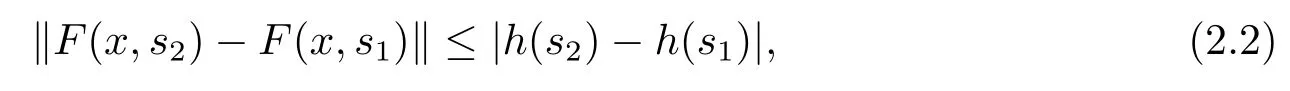
且對任意的(x,s1),(x,s2),(y,s1),(y,s2)∈Ω,有

引理 2.1[9]設F:Ω→Rn滿足(2.2)式,如果x:[α,β]→Rn,[α,β]?[t0,+∞)是方程(2.1)的一個解,則x在 [α,β]上有界變差,且并且在 [α,β]上x與函數h具有相同的連續性,其中表示x在[α,β]上的全變差.
引理2.2[10]假設f:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),對任意的τ0∈[t0,+∞),并且定義函數F:Ω→Rn為
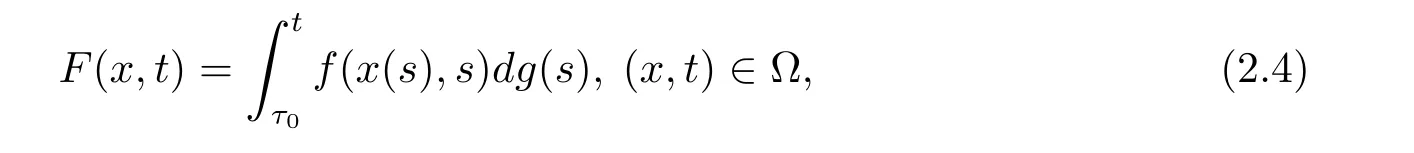
則F∈F(Ω,h),其中h:[t0,+∞)→R是不減的左連續函數,且
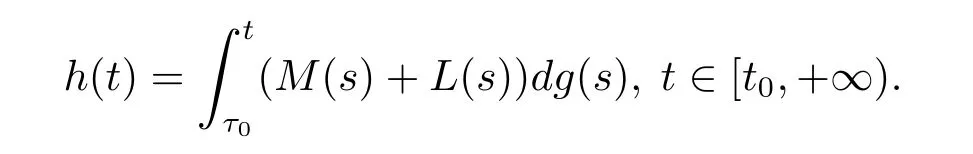
引理2.3[11]假設f:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),且p:[t0,+∞)→Rn滿足條件(H5)和(H6),對任意的τ0∈[t0,+∞),并且定義函數G:Ω→Rn為
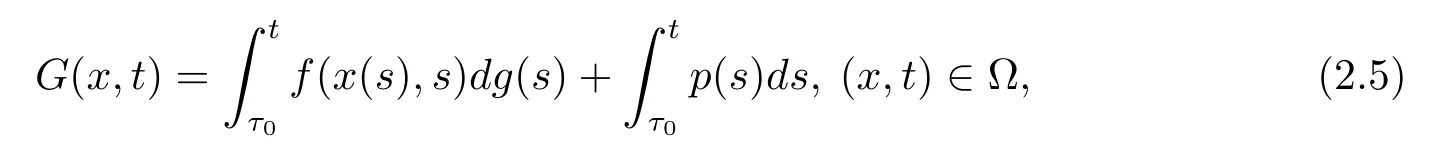
則G∈F(Ω,h),其中h:[t0,+∞)→R是不減的左連續函數,且
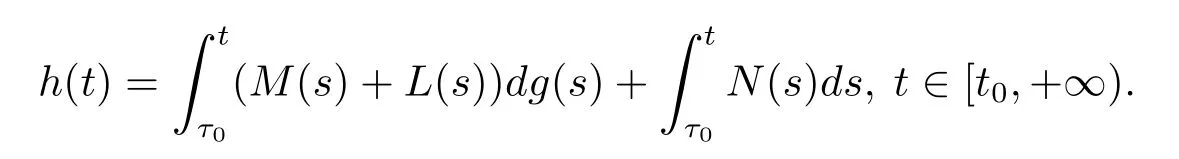
引理2.4[10]假設f:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),如果函數x:[a,b]→Rn,[a,b]?[t0,+∞)是測度微分方程(1.2)的解,當且僅當x是廣義常微分方程

在[a,b]上的解,其中函數F由(2.4)式給定.
引理2.5[11]假設f:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),且p:[t0,+∞)→Rn滿足條件(H5)和(H6),如果函數x:[a,b]→Rn,[a,b]?[t0,+∞)是測度微分方程(1.3)的解,當且僅當x是廣義常微分方程

在[a,b]上的解,其中函數G由(2.5)式給定.
引理 2.6[9]設F∈F(Ω,h),假設x:[α,β]→Rn,[α,β]?[t0,+∞)在 [α,β]上是有界變差函數,使得對每一個s∈[α,β],(x(s),s)∈Ω,則積分存在.
引理2.7[9]設F∈F(Ω,h),假設V:[t0,+∞)×Rn→R+是使得對任意的y∈Rn,函數V(·,y):[t0,+∞)→R+在(t0,+∞)上是左連續的,假設以下條件成立
(i)對任意的(t,x),(t,y)∈[t0,+∞)×Rn,常數L>0,有|V(t,x)-V(t,y)|≤L‖x-y‖.
(ii)存在一個實函數Φ:Rn→R,使得對于廣義常微分方程(2.6)在區間(a,b)?[t0,+∞)上的每一個解y:(a,b)→Rn,對于t∈(a,b),有
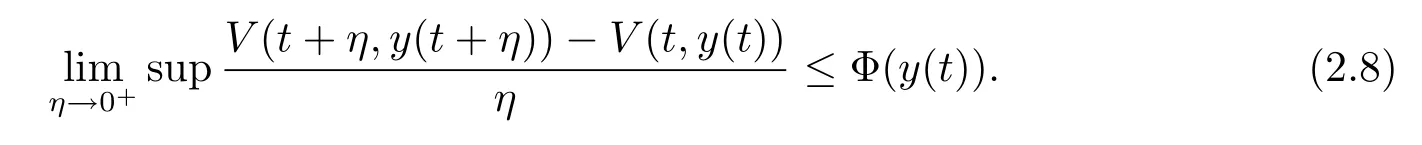
若:[α,β]→Rn,t0≤α<β<+∞是區間 [α,β]上的有界變差函數,并且在 (α,β]上是左連續的,則不等式
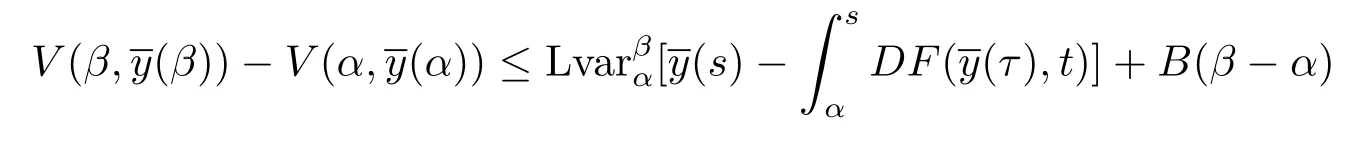
引理2.8[9]設G∈F(Ω,h),假設V:[t0,+∞)×Rn→R+是使得對任意的y∈Rn,函數V(·,y):[t0,+∞)→R+在(t0,+∞)上是左連續的,假設以下條件成立:
(i)對任意的(t,x),(t,y)∈[t0,+∞)×Rn,常數L>0,有|V(t,x)-V(t,y)|≤L‖x-y‖.
(ii)存在一個實函數Φ:Rn→R,使得對于廣義常微分方程(2.7)在區間(a,b)?[t0,+∞)上的每一個解y:(a,b)→Rn,對于t∈(a,b),有

若:[α,β]→Rn,t0≤α<β<+∞是區間 [α,β]上的有界變差函數,并且在 (α,β]上是左連續的,則不等式
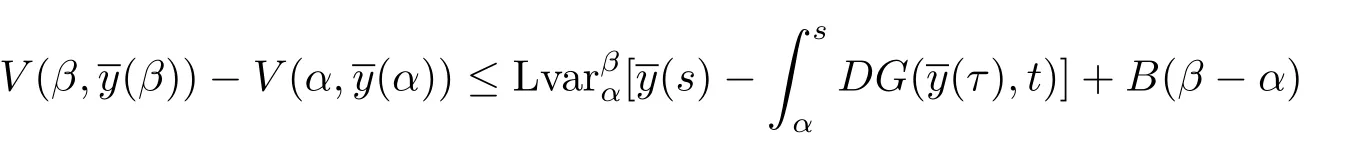
3 主要結果
本節定義了測度微分方程(1.2)及擾動后的測度微分方程(1.3)的變差一致Lipschitz穩定性,一致Lipschitz穩定性和一致整體Lipschitz穩定性.利用廣義常微分方程的Lipschitz穩定性結果給出了測度微分方程的變差一致Lipschitz穩定性,一致整體Lipschitz穩定性定理及其證明.
定義3.1測度微分方程(1.2)的平凡解x≡0是變差一致Lipschitz穩定的,若存在A>0,以及δ>0,使得若:[α,β]→Bc,t0≤α<β<+∞是 [α,β]上的有界變差函數,并且在(α,β]上左連續,當(α)‖<δ和

時,則有
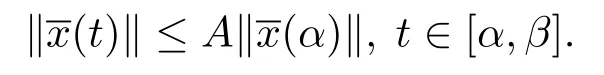
定義3.2測度微分方程(1.2)的平凡解x≡0是
(i)一致Lipschitz穩定的,若存在A>0,δ>0,使得若:[α,β]→Bc,t0≤α<β<+∞是測度微分方程(1.2)在[α,β]上的一個解,當(α)‖<δ時,則(t)‖ ≤(α)‖,t∈[α,β].
(ii)一致整體Lipschitz穩定的,若存在A>0,使得若:[α,β]→Bc,t0≤α<β<+∞是測度微分方程(1.2)在[α,β]上的一個解,則(t)‖ ≤(α)‖,t∈[α,β].
注若測度微分方程(1.2)的平凡解x≡0是變差一致Lipschitz穩定的,則它是一致Lipschitz穩定的.
定義3.3測度微分方程(1.3)的平凡解x≡0是變差一致Lipschitz穩定的,若存在A>0,以及δ>0,使得若:[α,β]→Bc,t0≤α<β<+∞是 [α,β]上的有界變差函數,并且在(α,β]上左連續,當(α)‖<δ和
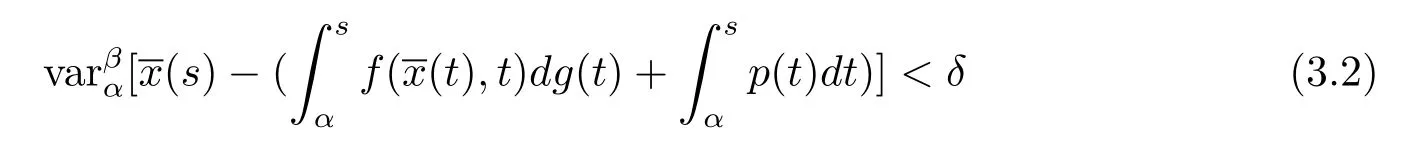
時,則有
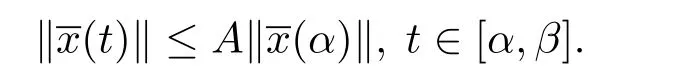
定義3.4測度微分方程(1.3)的平凡解x≡0是
(i)一致Lipschitz穩定的,若存在A>0,δ>0,使得若:[α,β]→Bc,t0≤α<β<+∞是測度微分方程(1.3)在[α,β]上的一個解,當(α)‖<δ時,則
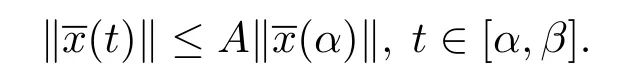
(ii)一致整體Lipschitz穩定的,若存在A>0,使得若:[α,β]→Bc,t0≤α<β<+∞是測度微分方程(1.3)在[α,β]上的一個解,則
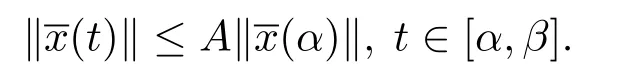
注若測度微分方程(1.3)的平凡解x≡0是變差一致Lipschitz穩定的,則它是一致Lipschitz穩定的.
定理3.1設,其中假設V滿足以下條件
(i)對所有的t∈[t0,+∞),有V(t,0)=0.
(iii)存在一個常數K>0,使得
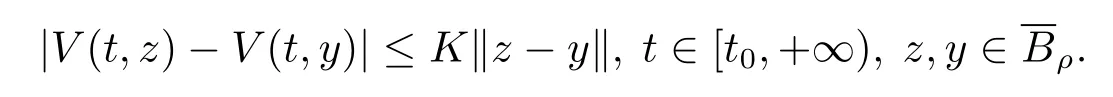
(iv)存在一個單調遞增函數b:[0,+∞)→[0,+∞)滿足b(0)=0,使得對所有的t∈[t0,+∞),有V(t,x)≥b(‖x‖).

則方程(1.2)的平凡解x≡0是變差一致Lipschitz穩定的.
證根據引理2.2,需驗證F∈F(Ω,h),F由(2.4)式給定,Ω=Bc×[t0,+∞).因為f:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),使得對任意的(x,s2),(x,s1)∈Ω,有

且對任意的(x,s2),(x,s1),(z,s2),(z,s1)∈Ω,由條件(H4),有

所以F∈F(Ω,h),其中τ∈[t,+∞),且h:[t,+∞)→R是000不減的左連續函數.
由引理2.4可知,測度微分方程(1.2)的解也是廣義常微分方程(2.6)的解,因此它們的解都是有界變差函數.
以下證明測度微分方程(1.2)的平凡解x≡0是變差一致Lipschitz穩定的.
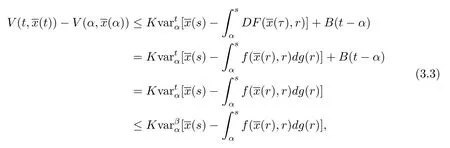
因為Φ≡0,所以且由條件(i)和(iii),有即

對于ε>0,使得不等式成立.設δ>0,使得 2Kδ<b(ε).若

因此由(3.3)和(3.4)式,有

由于2Kδ<b(ε),則有
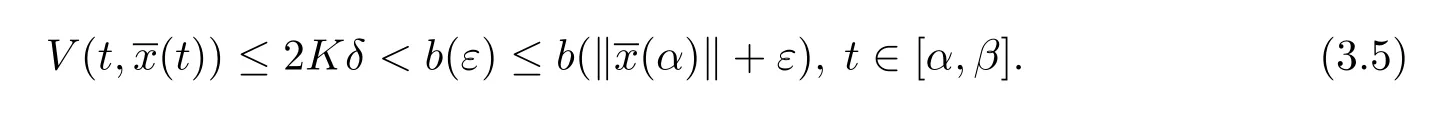
另外,由條件(iv),有
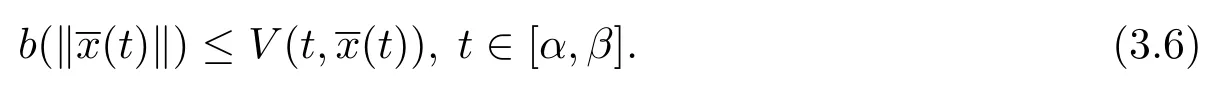
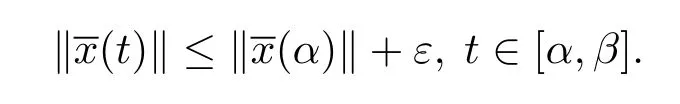
由定義3.1,取A=1,并且由ε的任意性,則滿足,則測度微分方程(1.2)的平凡解x≡0是變差一致Lipschitz穩定的.
定理3.2設滿足定理3.1中的條件(i),(ii),(iii)和(v),并且滿足條件
(iv′)對所有的,有V(t,x)≥‖x‖.
則方程(1.2)的平凡解x≡0是一致整體Lipschitz穩定的.
證設是測度微分方程 (1.2)在 [α,β]上的解.由條件(iii),(v)及引理2.4和引理2.7,其中Φ≡0,所以對任意的t∈[α,β],有
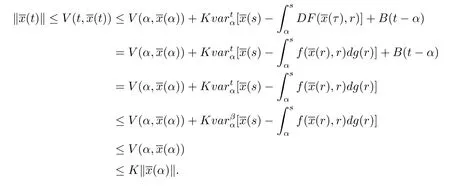
定理3.3設,其中假設V滿足以下條件
(i)對所有的t∈[t0,+∞),有V(t,0)=0.
(iii)存在一個常數K>0,使得
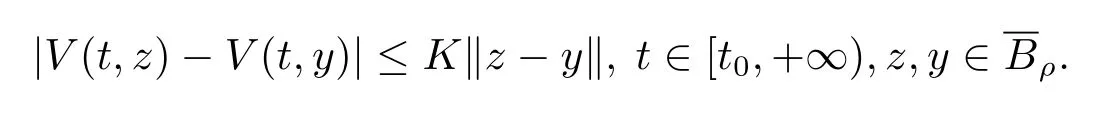
(iv)存在一個單調遞增函數b:[0,+∞)→[0,+∞)滿足b(0)=0,使得對所有的t∈[t0,+∞),有V(t,x)≥b(‖x‖).
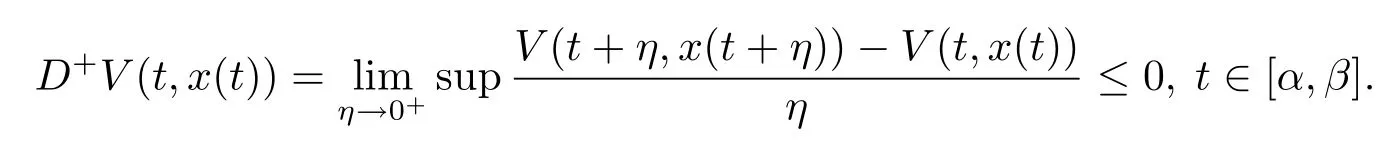
則方程(1.3)的平凡解x≡0是變差一致Lipschitz穩定的.
證根據引理2.3,需驗證G∈F(Ω,h),G由(2.5)式給定,Ω=Bc×[t0,+∞).因為f:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),p:[t0,+∞)→Rn滿足條件(H5)和(H6),使得對任意的(x,s2),(x,s1)∈Ω,有
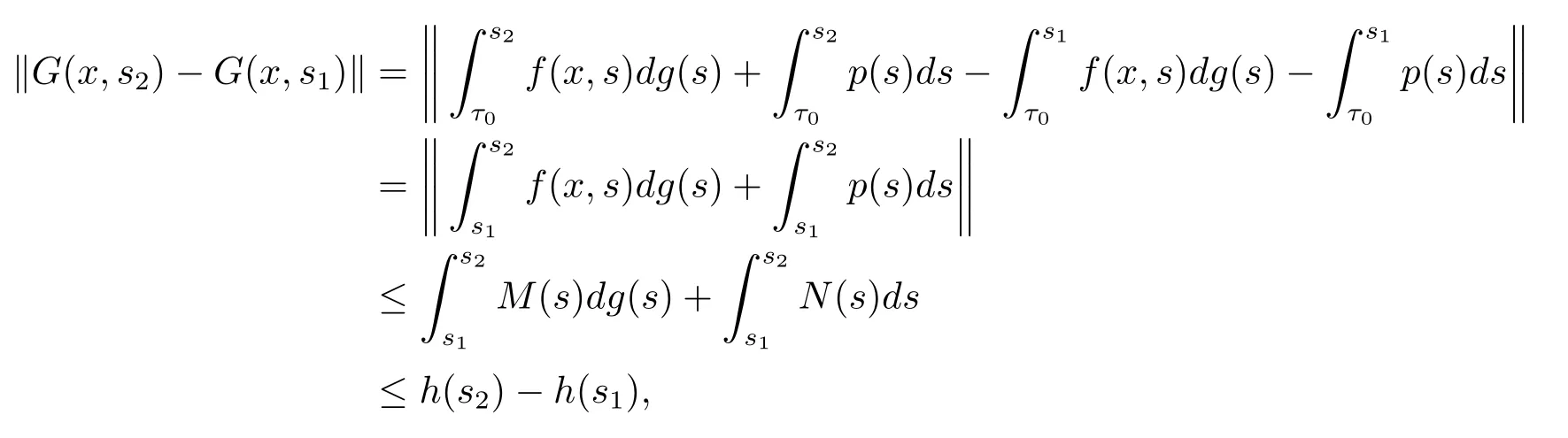
且對任意的(x,s2),(x,s1),(z,s2),(z,s1)∈Ω,由條件(H4),有
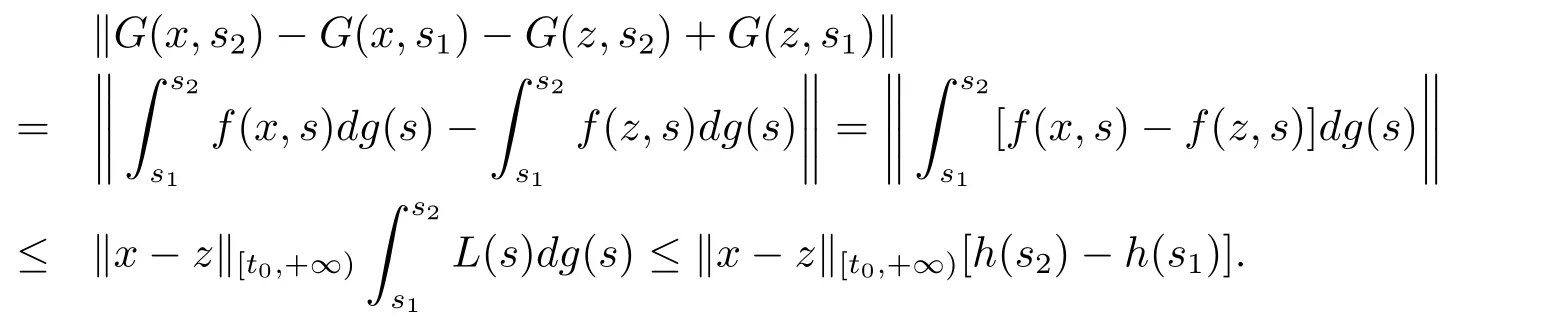
所以G∈F(Ω,h),其中τ0∈[t0,+∞),且h:[t0,+∞)→R是不減的左連續函數.
由引理2.5可知,測度微分方程(1.3)的解也是廣義常微分方程(2.7)的解,因此它們的解都是有界變差函數.
以下證明測度微分方程(1.3)的平凡解x≡0是變差一致Lipschitz穩定的.

因為Φ≡0,所以且由條件(i)和(iii),有即

對于ε>0,使得不等式成立.設δ>0,使得 2Kδ<b(ε).若
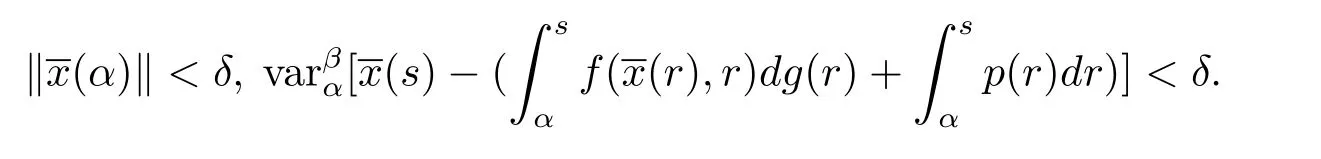
因此由(3.7)和(3.8)式,有
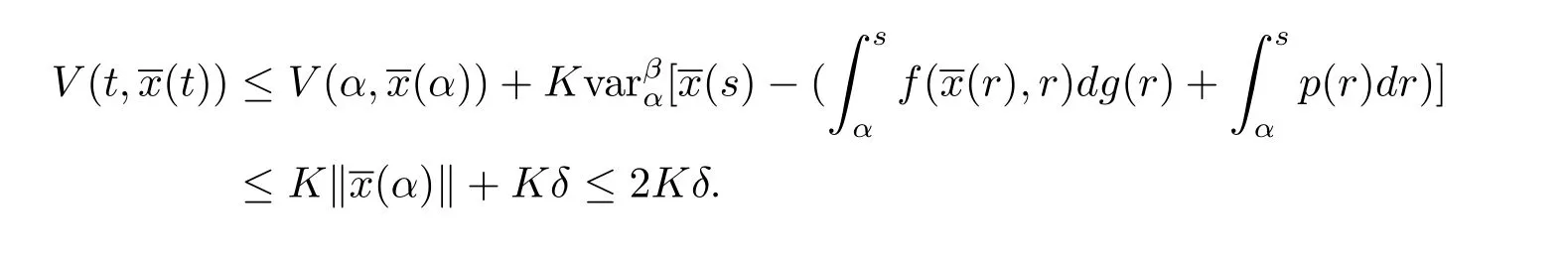
由于2Kδ<b(ε),則有
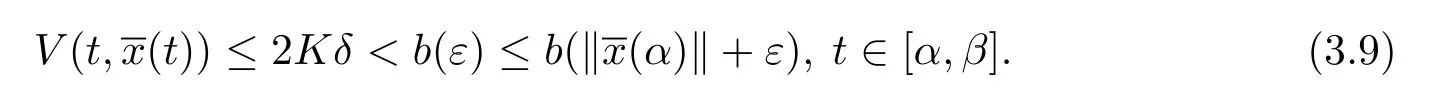
另外,由條件(iv),有
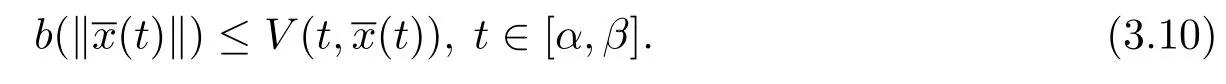
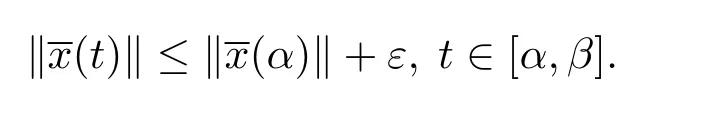
由定義3.3,取A=1,并且由ε的任意性,則滿足,則測度微分方程(1.3)的平凡解x≡0是變差一致Lipschitz穩定的.
定理3.4設滿足定理3.3中的條件(i),(ii),(iii)和(v),并且滿足條件:
(iv′)對所有的有V(t,x)≥‖x‖.
則方程(1.3)的平凡解x≡0是一致整體Lipschitz穩定的.
證設是測度微分方程 (1.3)在 [α,β]上的解.由條件(iii),(v)及引理2.5和引理2.8,其中Φ≡0,所以對任意的t∈[α,β],有