強基固本才能厚積薄發
——以幾道含參絕對值不等式求解為例

鄭夢華

江西師范大學數學與信息科學學院 (330022)

掌握數學基礎知識是解答數學問題的基礎，也是學生數學學習再創造、再發現的基礎.絕對值不等式是高中選修內容，而含參絕對值不等式是絕對值不等式的深化與補充.該類題型靈活多變，既考查參數又考查變量，綜合性較強;需要學生具有扎實的數學基礎知識，也需要學生具有較強的數學能力素養.本文通過幾例予以說明.

評注：本題主要考查絕對值基本定義及用定義去絕對值的方法，這是絕對值不等式中最基礎的知識和方法，其本質是簡化數學問題，強化學生對絕對值本質的理解.

例2 設函數f(x)=|x+1|+|2x-1|,g(x)=|3x-2m|+|3x-4|,若對?x1∈R,存在x2∈R,使得f(x1)=g(x2)成立，求實數m的取值范圍.

解析：由題意，設A={y|y=f(x)},B={y|y=g(x)}，則A?B.由f(x)=

評注：求解含參絕對值不等式問題最基本的數學思想方法是分類討論，本題除考查學生對該思想方法的運用,還考查到絕對值三角不等式的運用，同時,求解中運用的集合思想及數形結合思想也很重要.

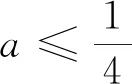
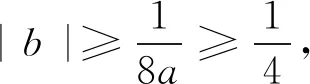
評注：本題涉及三個參變量，并且同時出現“任意”、“存在”兩個量詞，其本質是一個二次函數的最值問題，但在求解過程中需要運用到分類討論、數形結合等基本的數學思想方法,同時需要具有代換法及最值函數處理技巧等,其交匯綜合性較強.

正如新課標指出的：“數學教育幫助學生掌握現代生活和進一步學習所必需的數學知識、技能、思想和方法；提升學生的數學素養，促進學生思維能力、實踐能力和創新意識的發展.”數學問題解決教學應重在強化學生基礎知識、基本思想方法訓練的基礎上，培養學生善于綜合運用所學,巧解數學問題.