基于有限元方法的高速變軌距轉向架車軸磨損分析

胡飛飛，黃志輝，李國棟，周殿買，孔瑞晨

基于有限元方法的高速變軌距轉向架車軸磨損分析

胡飛飛1，黃志輝1，李國棟2，周殿買2，孔瑞晨2

（1. 西南交通大學，牽引動力國家重點實驗室，成都 610031；2. 中車長春軌道客車股份有限公司，長春 130062）

針對高速變軌距轉向架在運用過程中出現的車軸異常磨損問題，分析了造成車軸異常磨損的原因。基于Archard理論模型，推導了變軌距轉向架車軸表面磨損量的計算公式；運用有限元方法，利用HyperMesh與ANSYS軟件聯合仿真，建立車軸-滑動軸承的有限元分析模型，研究了垂向載荷、車軸-滑動軸承間隙配合值對車軸磨損量的影響。變軌距列車時速為250 km/h時，計算結果表明：垂向載荷以及車軸-滑動軸承間隙配合值越大，車軸表面磨損也越嚴重；當車軸-滑動軸承間隙配合值為0.15 mm且車軸端部受到垂向載荷110.31 kN作用時，列車運行30萬km后車軸的表面磨損量最高達0.480 mm。

變軌距；Archard模型；有限元；車軸磨損

0 引 言

變軌距轉向架是指在地面設施協助下，通過變軌機構改變輪對內側距的轉向架，相較于傳統的高速動車組轉向架，其輪軸結構發生了很大改變。變軌距轉向架在國外已有許多成功的運用情況[1]，但也存在不少問題。其中，車軸表面異常磨損的問題在波蘭、日本等國的變軌距轉向架上均有出現，但是至今都沒有得到完美解決[2]。波蘭的運用公司曾經研究過其開發的SUW200型變軌距輪對車軸的磨耗情況，發現轉向架在運行10萬km后，車軸的平均磨損量在0.199~0.318 mm之間[3]，技術人員分析認為車軸的彎曲變形和輪軸間隙的存在是造成車軸磨損的主要原因。日本變軌距轉向架歷經三代的發展，每代變軌距轉向架在運用考核中均出現過車軸異常磨損的問題[4, 5]。第三代變軌距轉向架在累計行駛3.3萬km時就發現了車軸表面的異常磨損，技術人員同樣認為車軸的彎曲變形與輪軸間隙是造成車軸異常磨損的主要原因，并就此提出過一些解決辦法。

國內對變軌距轉向架的研究起步較晚，尚處在最初的概念設計階段，還沒有人對變軌距轉向架車軸的磨損問題進行過深入探索和研究。本文以時速250 km/h高速變軌距轉向架的輪軸結構為基礎，分析車軸表面異常磨損的原因，并運用有限元方法，研究這些因素對車軸磨損量的影響。

1 輪軸結構簡介及車軸磨損原因分析

1.1 變軌距轉向架輪軸結構簡介

與傳統轉向架輪軸結構相比，變軌距輪對車輪與車軸過盈配合的關系已經不復存在，兩者間扭矩的傳遞是通過花鍵配合實現的[6, 7]。某變軌距轉向架輪軸結構如圖1所示。

圖1 某變軌距轉向架輪軸局部結構示意

圖1所示各部件的配合關系為：車軸與滑移襯套通過花鍵連接，與滑動軸承為間隙配合關系；滑移襯套與車輪、滑動軸承以及軸箱軸承都是過盈配合關系。在滑移襯套與車軸間增設滑動軸承的主要目的是減小車輪、滑移襯套等部件在變軌時軸向滑移的摩擦阻力，利于轉向架變軌動作的完成。變軌距轉向架上扭矩的傳遞路徑如圖2所示。

圖2 變軌距轉向架上扭矩的傳遞路徑

1.2 變軌距轉向架車軸表面異常磨損原因分析

變軌距轉向架車軸異常磨損的原因主要有兩個：

第一，轉向架在變軌時，滑動軸承可在車軸上滑移，車軸與滑動軸承相互接觸產生摩擦磨損。由于此部分磨損只存在于轉向架進行變軌動作的時候，而轉向架正常運營時每天進行的變軌次數很少，所以本文在有限元分析時沒有考慮由變軌動作產生的磨損。

其二，車體上的垂向載荷通過路徑：二系懸掛→構架側梁→軸箱（一系懸掛）→軸箱軸承→滑移襯套→滑動軸承，最終將垂向載荷傳遞到車軸端部。車軸在垂向載荷的作用下發生彎曲變形與滑動軸承接觸，由于應力集中造成了車軸的異常磨損。同時，鑒于車軸與滑動軸承的間隙配合關系，轉向架正常運行時車軸外表面與滑動軸承內表面存在線速度差異，從而造成兩者間的旋轉磨損。車軸在垂向載荷作用下的彎曲變形如圖3所示，車軸與滑動軸承間隙配合示意如圖4所示。

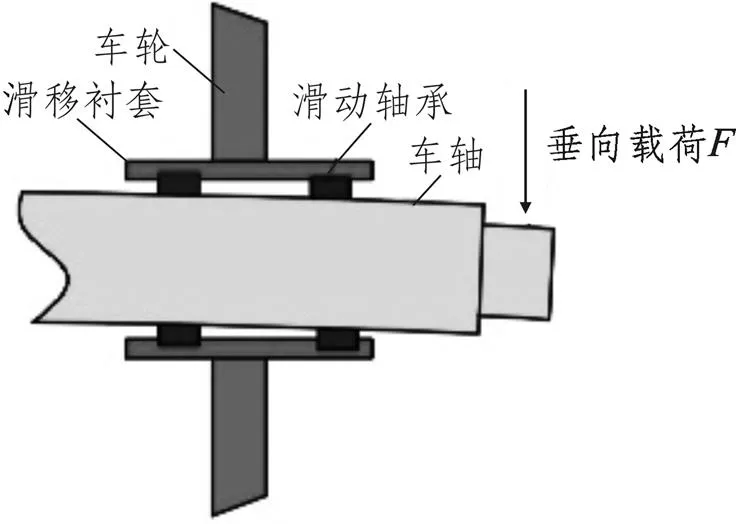
圖3 車軸彎曲變形

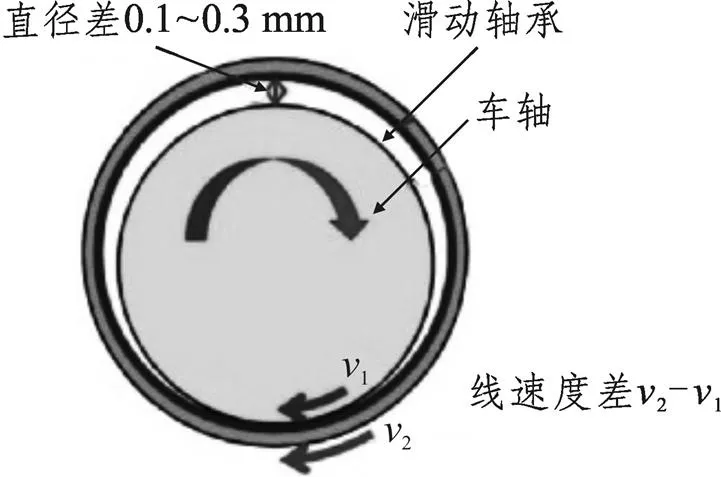
圖4 間隙配合線速度差

2 基于Archard理論的磨損量計算公式推導

Archard理論廣泛地應用于材料的磨損分析[8]，該理論認為材料的磨損量與法向壓力、相對滑移距離以及材料硬度有關[9, 10]，其一般表達式為：

由于車軸與滑動軸承之間的接觸壓力隨著兩者的轉動不斷發生變化，因此對（1）式微分得到的公式如下：

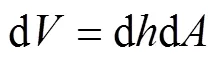
將（3）式代入到（1）式，整理得下式：

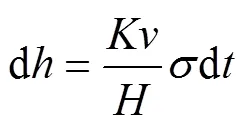
有限元分析得到了結點的迭代應力后，根據接觸壓力的分布情況對車軸與滑動軸承的接觸區域進行劃分，將接觸壓力分布均勻的結點劃分為一個區域。若將車軸旋轉一周的時間定義為一個磨損步長，則接觸區域內的結點在一個磨損步長內的磨損量計算公式為：

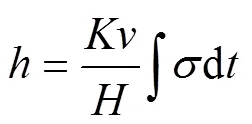
上式計算得到的只是單個結點在一個磨損步長內的磨損量，而車軸表面磨損量的計算公式為：

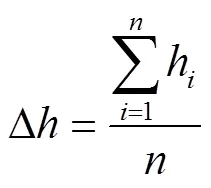
為計算列車運行一定里程后車軸的表面磨損量，假定列車在該區間內勻速運行且車軸在每個磨損步長內的磨損量是相等的，則總的磨損量計算公式為：

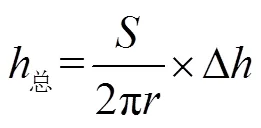
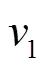
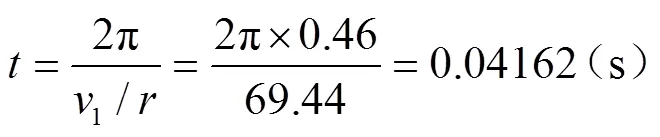
總的磨損步長數量為：

3 有限元模型的建立及載荷計算

3.1 有限元模型的建立

為了對車軸磨損量進行定量計算分析，利用HyperMesh軟件建立了車軸-滑動軸承有限元模型，如圖5所示。有限元模型載荷與約束的施加位置如圖6所示。

圖5 車軸-滑動軸承有限元模型

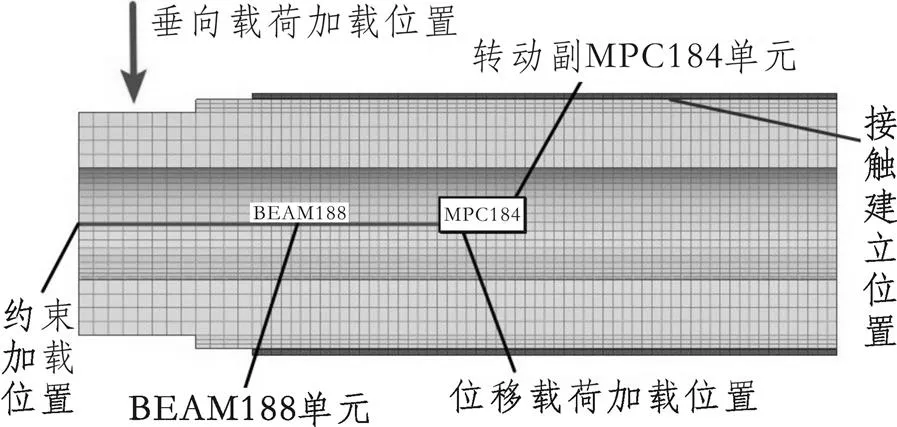
圖6 有限元模型邊界條件

圖5中的有限元模型包括車軸與滑動軸承間隙配合部位以及車軸端部位置，車軸端部的外花鍵齒不是本文的研究重點，故沒有畫出。車軸、滑動軸承均采用SOLID186線性六面體實體網格離散，最終的有限元模型共有241 878個單元和273 178個結點。

如圖6所示，由于SOLID186單元沒有轉動自由度，為了給模型施加旋轉位移載荷，引入了轉動副MPC184單元，同時還建立了BEAM188梁單元支撐有限元模型。轉動副單元的一個結點與車軸相互耦合，另一個結點與BEAM188單元的一端相互耦合。位移載荷施加在MPC184單元上，垂向載荷則施加于車軸端部位置，最后約束梁單元自由端結點的自由度作為模型的邊界條件。

在車軸外表面與滑動軸承內表面之間建立接觸關系，并用TARGE170單元與CONTA173單元來模擬[12]。將滑動軸承內表面設置為目標面，車軸外表面設置為接觸面，通過調節參數CNOF（接觸面的偏移值）的數值來控制間隙配合值的大小，接觸類型設置為面-面接觸[13, 14]。為保證計算精度，在進行網格劃分時盡量保證接觸區域內結點的相互對應。

考慮到滑動軸承內表面附著有0.5 mm的合成樹脂，該材料耐潮、不膨脹，在變軌時起潤滑作用，所以在此處對滑動軸承的有限元模型做局部加密處理，如圖7所示。

圖7 滑動軸承有限元模型局部加密

車軸材料采用EA4T鋼，滑動軸承采用45鋼，有限元模型材料參數見表1。

表1 材料屬性

3.2 載荷計算

本文考慮的載荷主要有兩個方面：

① 車軸端部受到垂向載荷作用，垂向載荷的大小由標準EN13749—2005[15]確定，將構架所受垂向載荷換算到車軸端部，得到的垂向載荷有以下幾種工況：110.31 kN、100.34 kN、95.86 kN、90.37 kN、85.04 kN。

② 給車軸與滑動軸承施加驅動載荷，使之旋轉。采用MPC接觸算法實現模型的旋轉運動，將驅動載荷以位移載荷的形式施加到有限元模型上，位移載荷隨時間的變化關系為：

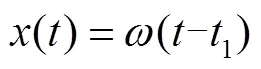
磨損分析是一個瞬態的分析過程，本文分為兩個載荷步加載：第一個載荷步，在車軸端部施加垂向載荷，使車軸與滑動軸承充分接觸；第二個載荷步，給有限元模型施加驅動載荷，模型進行旋轉運動。

為簡化計算，根據接觸壓力的分布情況劃分出多個接觸區域，用每個區域內接觸壓力最大結點的磨損量來表征每個區域的磨損情況，最終得到的車軸磨損量為多個接觸區域的平均磨損量。

4 有限元計算結果

4.1 車軸磨損有限元分析過程

當列車以時速250 km/h勻速運行時，以車軸端部受到垂向載荷110.31 kN且車軸與滑動軸承間隙配合值為0.15 mm為例，對車軸磨損量的計算過程進行詳細介紹，如下所示：

① 對接觸區域進行劃分

利用ANSYS的后處理功能，找到一個磨損步長內車軸與滑動軸承接觸壓力最大的時間點，此時車軸與滑動軸承的接觸狀態如圖8所示。根據接觸面上接觸壓力的分布情況，將接觸壓力分布均勻的區域單獨劃分出來，取每個區域上的最大壓力結點進行磨損計算。根據以上接觸點的選取原則，圖8總共劃分出4個接觸區域，將每個接觸區域上接觸壓力最大的結點分別編號為a、b、c、d。

圖8 車軸與滑動軸承接觸狀態

② 接觸壓力隨時間的變化關系

提取結點a、b、c、d接觸壓力隨時間的變化關系，結果如圖9~圖12所示。

根據積分的實際意義，式（5）中結點接觸壓力對時間的積分結果可用圖9~圖12中曲線與橫坐標軸圍成的面積來表示。

圖9 結點a接觸壓力隨時間的變化關系

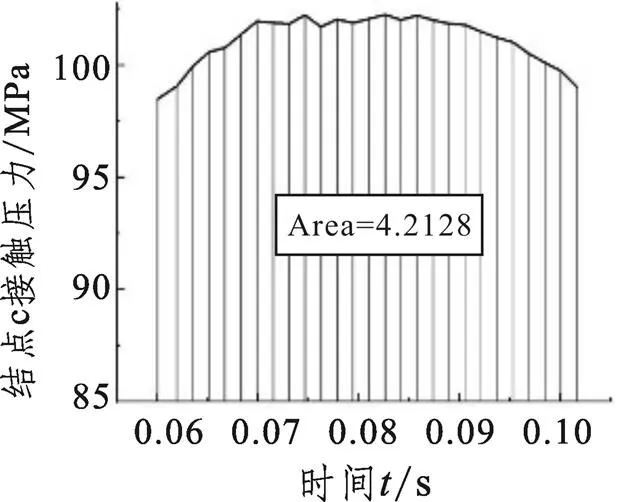
圖11 結點c接觸壓力隨時間的變化關系

圖12 結點d接觸壓力隨時間的變化關系

③ 計算結點磨損量

按式（5）計算結點a、b、c、d在一個磨損步長內的磨損量：

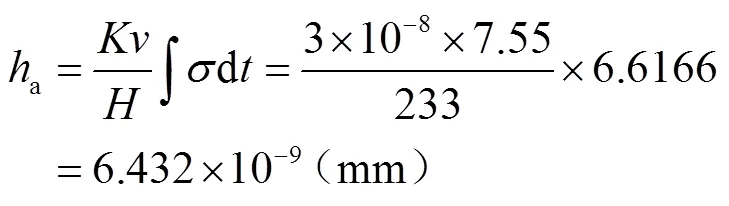
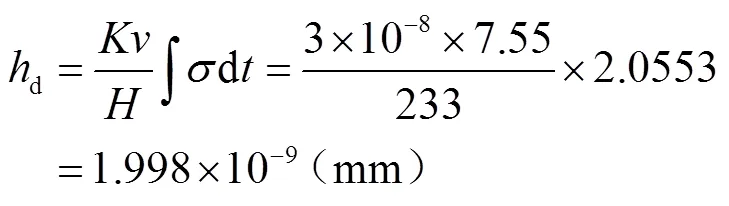
④ 計算結點平均磨損量

按式（6）計算車軸在一個磨損步長內的平均磨損量：

⑤ 計算車軸總磨損量

按式（7）計算列車以時速250 km/h運行30萬km后車軸表面的總磨損量：

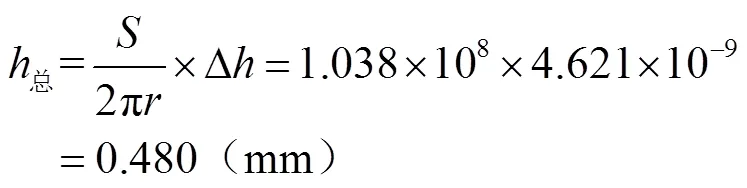
4.2 垂向載荷對車軸磨損的影響

當列車時速為250 km/h且車軸與滑動軸承間隙配合值為0.15 mm時，車軸端部在不同大小的垂向載荷作用下車軸磨損量的計算結果如圖13所示。

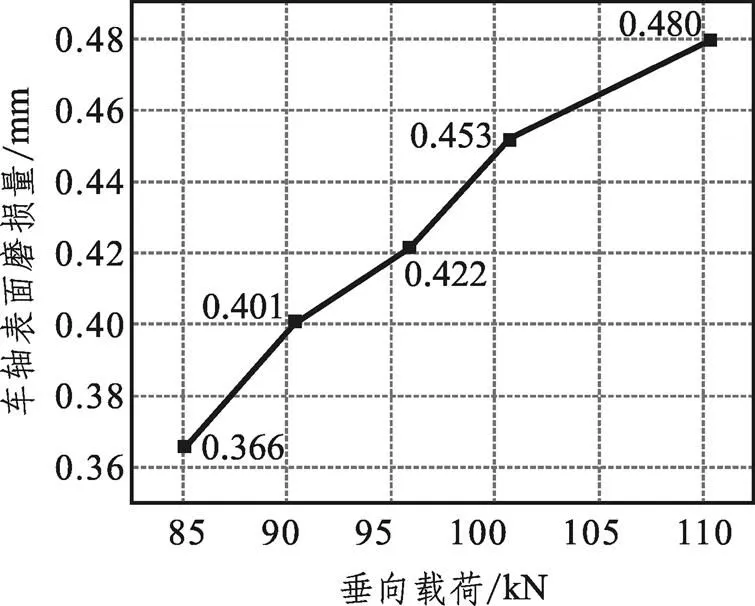
圖13 不同垂向載荷作用下車軸磨損量計算結果

如圖13所示，車軸表面磨損量隨著垂向載荷的增大而增加，這是由于垂向載荷的大小影響車軸與滑動軸承的接觸狀態，即垂向載荷越大，接觸壓力也越大，車軸上的應力集中程度越大，所以車軸的磨損量也越大。

4.3 車軸-滑動軸承間隙配合值對車軸磨損的影響

當列車時速為250 km/h且車軸端部受到的垂向載荷為110.31 kN時，不同車軸-滑動軸承間隙配合值下車軸磨損量的計算結果如圖14所示。

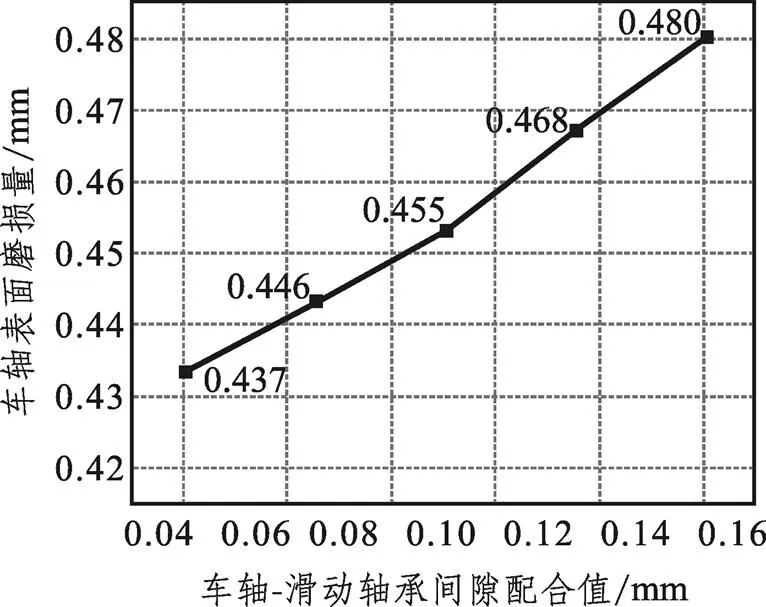
圖14 不同間隙配合值下車軸磨損量計算結果

由圖14可知，車軸磨損量隨車軸-滑動軸承的間隙配合值增大而增大。這是由于間隙配合值的大小影響車軸與滑動軸承的相對線速度差，即間隙值越大，兩者的相對線速度差也越大，所以車軸的磨損量也越大。

5 結 論

本文運用有限元方法，研究了時速250 km/h下變軌距轉向架車軸表面的磨損問題，分析了垂向載荷、車軸-滑動軸承間隙配合值對磨損量造成的影響，現得到以下結論：

① 當車軸-滑動軸承間隙配合值恒為0.15 mm，車軸端部所受的垂向載荷由85.04 kN增大為110.31 kN時，車軸磨損量從0.366 mm增加至0.480 mm，增幅達31%；當垂向載荷恒為最大值110.31 kN，車軸-滑動軸承間隙配合值從0.05 mm增大為0.15 mm時，車軸磨損量從0.437 mm增加至0.480 m，增幅約為10%。

② 垂向載荷的大小對變軌距車軸磨損量的計算結果有著顯著影響，而車軸-滑動軸承間隙配合值的變化對車軸磨損量的影響相對較弱，但仍然不可忽視。

[1] 李芾, 邵亞堂, 黃運華, 等. 國外變軌距列車及其轉向架的發展與研究[J]. 機車電傳動, 2018 (3): 1-13.

[2] 周殿買, 黃志輝, 徐彬, 等. 國外典型變軌距轉向架輪軸間的磨耗分析[J]. 機車電傳動, 2018 (6): 42-45.

[3] SZKODA M, MICHNEJ M. A method of fretting wear reduction in an automatic wheel set gauge change system[J]. Engineering Failure Analysis, 2014, 45: 363-375.

[4] 江崎秀明, 加賀谷博昭, 山城秀夫, 等. 軌間可変臺車の高速走行安定性解析[C]//日本機械學會論文集C編. [S. l. ]: [s. n. ], 2013: 1859-1871.

[5] 軌間可変技術評価委員會. 軌間可変電車の技術開発に関する技術評価[R]. 東京: 軌間可技術評委員仝, 2010 (平成22年).

[6] 徐芳, 黃志輝, 王瑞卓, 等. 1435/1000 mm變軌距動車組轉向架設計[J]. 機車電傳動, 2019 (4): 1-6.

[7] 黃志輝, 夏朝國, 胡飛飛, 等. 變軌距輪對軸套式花鍵的設計[J]. 機車電傳動, 2018 (4): 1-5.

[8] 胡建軍, 侯天鳳. 穩態變形下Archard模型模具磨損數值分析 (英文) [J]. 機床與液壓, 2014, 42 (18): 46-49.

[9] 李聰波, 何嬌, 杜彥斌, 等. 基于Archard模型的機床導軌磨損模型及有限元分析[J]. 機械工程學報, 2016, 52 (15): 106-113.

[10] 徐向紅, 湯文成, 俞濤, 等. 基于Archard理論的滾珠絲杠磨損預測[J]. 組合機床與自動化加工技術, 2016 (2): 54-59.

[11] 桂長林. Archard的磨損設計計算模型及其應用方法[J]. 潤滑與密封, 1990 (1): 12-21.

[12] 高恒強, 蔡紅娟, 蔡苗. 基于Archard修正模型的角接觸球軸承磨損有限元分析[J]. 機床與液壓, 2018, 46 (15): 159-164.

[13] 鄒紀操, 傅茂海, 李朝曦, 等. 高速變軌距動車組轉向架滑動套配合量影響研究[J]. 機車電傳動, 2018 (5): 1-4.

[14] 顏東煌, 劉雪鋒, 田仲初, 等. 銷軸連接結構的接觸應力分析[J]. 工程力學, 2008 (1): 229-234.

[15] European Committee for Standardization. EN 13749: 2005 railway applications-methods of specifying structural requirements of bogie frames[S]. London: British Standards Institution, 2005.

Analysis of Axle Wear in High-speed Variable Gauge Bogies Based on the Finite Element Method

HU Fei-fei1, HUANG Zhi-hui1, LI Guo-dong2, ZHOU Dian-mai2, KONG Rui-cheng2

（1. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China; 2. CRRC Changchun Railway Vehicles Co., Ltd., Changchun 130062, China）

In this study, abnormal wear of axles during the operation of high-speed variable gauge bogies was analyzed. Based on the Archard theoretical model, the calculation formula for axle surface wear in a variable gauge bogie was derived. A finite element analysis model of axle sliding bearing was established via the finite element method and a joint simulation using HyperMesh and ANSYS software. The effect of vertical load and clearance fit value of axle sliding bearing on axle wear was examined. When the speed of variable gauge bogie was 250 km/h, the results indicated that as the vertical load and clearance fit between the axle and sliding bearing increase, the severity of surface wear of the axle increases. Furthermore, when the fit value of the clearance between the axle and sliding bearing was 0.15 mm and the end of the axle was subjected to a vertical load of 110.31 kN, the maximum surface wear of the axle was 0.480 mm after the train operated for 300 000 km.

variable gauge; Archard method; finite element method; axle wear

U270.33

A

10.3969/j.issn.1672-4747.2020.03.006

1672-4747（2020）03-0050-08

2019-11-09

國家重點研發計劃（2016YFB1200501）

胡飛飛（1995—），男，漢族，碩士研究生，主要從事結構與強度方面的研究，E-mail：hff510525@163. com

黃志輝，（1966—），男，漢族，博士，研究員，研究方向：機車車輛結構與設計理論、系統動力學、結構與強度方面等，E-mail：hzh_95@163. com

胡飛飛，黃志輝，李國棟，等. 基于有限元方法的高速變軌距轉向架車軸磨損分析[J]. 交通運輸工程與信息學報，2020，18（3）：50-56, 152

（責任編輯：劉娉婷）