信息工具對高中數學教學的影響和輔佐

陳瑜

[摘? 要] 高中數學的抽象性與嚴謹性，對于培養學生的思考能力以及邏輯思維能力有著非常重要的作用. 然而傳統的數學教學方式存在著不少的缺陷，對于高中數學的教學效果造成了不良的影響. 通過信息工具在高中數學教學中的應用，可以對傳統教學方式中的不足進行補充，使高中數學教學質量得到較大的提高. 文章對于高中數學教學中信息工具的應用現狀進行了分析，指導教師如何有效運用現代教育技術來指導高中數學學科教學實踐，指導師生要關注信息時代大環境下的教學改革，為教學提供了理論指導和科學論證.

[關鍵詞] 信息工具;高中數學;影響;輔佐

信息技術的飛速發展，正悄悄地改變著我們的生活環境和學習方式. 信息技術不僅為我們提供了一種全新的教育模式，也是對傳統教育的一種挑戰. 如何有效地運用現代教育技術來指導高中數學學科教學實踐，既是一個熱點問題，也是學科課程改革的難點問題. 《普通高中數學課程標準（2017年版）》的修訂原則里，明確要求新課標要反映先進的教育思想和理念. 在信息時代的大環境下，學生擁有多樣化的學習和發展需求，關注信息化環境下的教學改革，為我們的教學提供了理論指導和科學論證.

新課標對信息工具與信息技術的強調

新課標強調的“數學學科核心素養”以及“四基”“四能”，是數學課程目標的集中體現，六大核心素養里也處處滲透著信息技術的使用. 比如數學抽象，需要在熟悉的情境中進行抽象，借助大量的事例來幫助學生進行概括，積累從具體到抽象的活動經驗;直觀想象借助空間形式認識事物，現代背景下可以借助多種信息工具，帶給我們過去所不能做到的直觀形象;數學建模強調真實背景下的數學，是數學應用的重要形式，信息工具的介入，為培養學生的創新意識和科學精神，應用數學解決實際數學注入了新的活力. 所有這些都告訴我們，信息技術融合在數學教學的方方面面，對改進和完善教學活動具有重要作用.

高中教學中常用信息工具簡介

1. 課堂教學層面上

很多學校都有大屏幕的觸屏或者投影，很多教師用了閱卷系統，運用大數據進行更深入更全面的分析. 除了這些以外，還有所謂的微課、翻轉課堂等，學生常用的APP類如“小猿搜題”等. 有的學校里，學生可以利用平板電腦做一些工作，比如在課前可以通過平板派發一些資料和學習的內容給學生，課中可以組織學生進行互動、投票、做筆記等，課后可以派發練習、做測試，選擇題可以自動批閱，還可以把不同的答案進行歸類……這樣，信息工具的運用可以延伸到課前、課中與課后.

2. 數學教學設計層面上

信息工具在數學課堂中的運用，是指教師在課堂教學設計中，很自然地運用一些技術工具，比如常見的幾何畫板、GeoGebra、圖形計算器等. 有的教師擔心技術工具會削弱學生的計算能力，其實核心素養里關于數學運算這一塊，就要求選擇適當的算法，運用適當的工具進行計算，像電子表格等，這些將直接影響到我們學習的工具.

信息技術在高中數學教學中的應用現狀

蘇教版普通高中課程標準實驗教科書中，多處使用信息工具來進行數學課堂教學，比如“指數函數、對數函數圖像”，課標就明確要求要由計算工具畫出具體的函數圖像. 在二分法、統計這些內容上，計算器和計算機更是在大量數據的處理中發揮了不可替代的作用. 人教A版的新教材里面，專門有信息技術應用的欄目，這個欄目里面涉及的內容，包括畫函數圖像、計算機代數系統的應用、統計軟件、動態幾何軟件的運用等，都專門做了要求. 除了這些以外，課本里還有一個欄目是數學的探究活動，里面有很多東西需要用到技術工具來處理. 也就是說，從課標的要求，到具體的實施，再到教材的落實，信息技術融合在教學的方方面面，細化到教學的整個內容當中，用技術工具來處理具體的內容.

信息工具與數學課堂教學的整合實例研究——利用幾何畫板對函數y=x+■（a>0）性質的研究

對勾函數是高中數學練習中經常出現的一類函數，人教A版新版數學教材中，新增了內容“探究與發現：探究函數y=x+■的圖像與性質”. 在補充介紹對勾函數y=x+■（a>0）的性質時，筆者采用讓學生動手操作，從實踐中感悟真知的策略.

師：請同學們利用幾何畫板程序，畫出y=x+■的圖像，并從圖像中觀察，歸納該函數的基本性質.

生1：該函數圖像的形狀如同“雙勾”，因此取名為“對勾函數”.

生2：該函數圖像關于原點對稱，因此它是奇函數.

生3：該函數的主要性質包括：定義域、值域、單調性、奇偶性等. 由圖像觀察可知，該函數的定義域和值域均為（-∞，0）∪（0，+∞），在（-∞，-1）和（1，+∞）上單調遞增，在（-1，0）和（0，1）上單調遞減，它的圖像關于原點對稱，所以它是奇函數.

師：y=x+■是對勾函數y=x+■（a>0）的一個特例，通過修改參數a的值，函數圖像會有什么變化？為什么要規定a>0的條件呢？

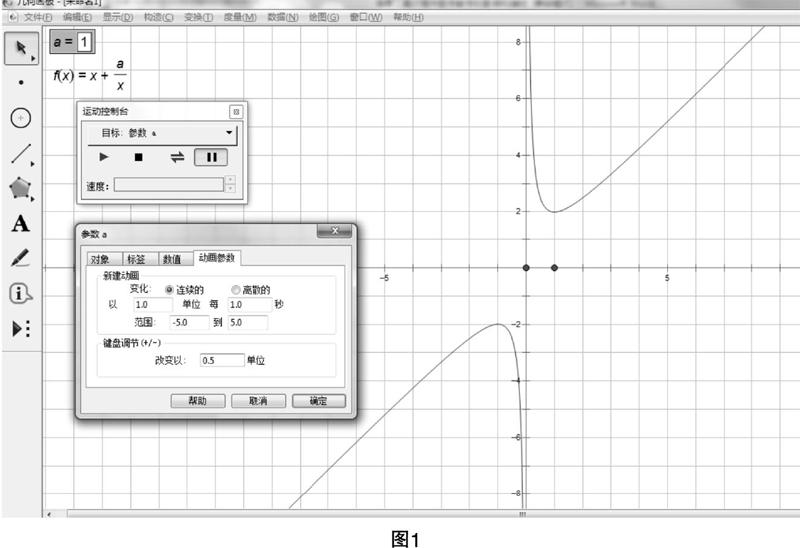
生4：從圖像上看，當a的值不斷變大時，圖像的形狀逐漸向左下方和右上方偏移;當a=0時，y=x是一次函數;當a<0時，圖像的形狀發生了改變，在（-∞，0）和（0，+∞）上均為單調遞增. （如圖1所示）

這時候，有的學生饒有興致地把圖像的動態變化過程反復演示了幾遍后，又有了新的發現.

生5：在圖像的變化過程中，可以觀察到，圖像中心部分的變化較大，而兩側部分的變化并不明顯，由此可以猜想：y=x是函數y=x+■（a>0）兩側部分的漸近線.

師：是不是這樣呢？我們來證明一下：當x>0時，y=x+■（a>0），說明函數右半部分的圖像y=x在圖像的上方;而當x→+∞時，■→0，因此對勾函數圖像向右越來越靠近y=x. 根據奇函數圖像的對稱性，可類似得到左半部分的圖像和性質.

師：我們通過觀察圖像，可以直觀地得到函數的這些基本性質，甚至可以大膽地猜測原來我們不知道、不熟悉的性質，但是我們說“大膽猜想，小心求證”，再輔之以嚴密的推理，從代數的角度進一步論證了相關結論的正確性，這正是“數缺形時少直觀，形缺數時難入微”.

信息工具（幾何畫板）的引入和使用，容易引起學生的學習興趣. 在信息技術環境下，教師由講授者轉型為引導者，學生由被動接受知識轉變為主動探究知識. 教師將以往的教學內容重新進行整合和組織，學生從新的角度去探究問題，在動態變化的過程中認識到數學概念的本質，在活動過程中積累了經驗，對于相關知識點將會理解得更透徹、更清晰.

信息工具在未來數學教學中的前景展望

不管教師有沒有做好充分的心理準備，信息技術工具已經在不斷地滲透著我們的課堂內外. 比如現在很多學校都有的大屏幕的觸屏或者投影，很多教師都用過閱卷系統. 除此以外，我們教師熟悉的微課，學生熟悉的各種學習類APP，很多東西都在不斷地變革著我們的課堂. 筆者認為，信息技術的運用，是指教師在課堂中很自然地運用一些技術工具，從而增強教學的直觀性，啟發學生的創新思維，激發學生的學習熱情. 目前我們的信息技術還用得不夠廣泛和普及，這與我們教師的認識水平以及培訓不夠深入有關系. 相信隨著技術的發展，國家對技術要求的不斷提升，對于教師培訓的廣度和深度一定會有很大發展. 教師要有一種積極的態度，迎接這項富有挑戰性的工作，需要投入巨大的熱情和科學的態度，讓技術伴隨教師成長，讓師生在信息工具的應用中獲得更大的體會和感悟.