解析突破,思維導引,教學微設
陳宣新
[摘? 要] 在教學中需要借助考題來提升學生的綜合能力,解析幾何題能夠全面考查學生的知識水平和思維能力.解析幾何題的綜合性較強,建議采用思路呈現、繪制思維導圖、教學微設計的方式,通過設問引導,問題拆解來還原解題過程,文章以一道解析幾何考題為例開展解題教學探討.
[關鍵詞] 解析幾何;綜合;平行四邊形;思維導圖;思維
解析幾何是高中數學的核心內容,也是高考壓軸題的命題點,常以綜合題的形式出現. 筆者認為提高學生解決解析幾何問題的能力,應從解題策略講解入手,幫助學生形成正確的解題思維. 因此在考題教學中應立足問題考點,解構問題思維,開展問題反思,提煉數學思想.下面以一道解析幾何考題為例進行探究.
考題呈現
例題:已知橢圓C的解析式為9x2+y2=m2(m>0),直線l不經過原點O,且不與坐標軸相平行,設直線l與橢圓C的兩個交點分別為A和B,點M為線段AB的中點,試回答下列問題.
(1)連接OM,試證明直線OM的斜率與直線l的斜率之積為定值.
(2)設直線l經過點■,m,延長線段OM,設與橢圓C的交點為點P,試分析四邊形OAPB能否為平行四邊形?如果能,請求出此時直線l的斜率;如果不能,請說明理由.
思路突破
第(1)問求證直線OM和l的斜率之積為定值,突破難點有兩個:一是直線l的方程未知,二是點M的坐標未知.考慮到點M與點A和B的坐標相關,而點A和B是直線l與橢圓C的交點,因此問題實質就是研究直線與橢圓的相交問題,常用的策略是設而不求,韋達定理簡化.因此求解時可以按照如下思路進行:首先設出直線l的方程,然后聯立直線l與橢圓C的方程,方程的解就是點A和B的橫坐標值,然后利用韋達定理構建點M的坐標,從而求出直線OM的斜率,最后對兩直線斜率之積進行化簡即可.
設直線l的方程為y=kx+b(k和b均不為0),點A(x1,y1),B(x2,y2),則點M■,■. 聯立直線l與橢圓C的方程:y=kx+b,9x2+y2=m2,消去y,整理可得(k2+9)x2+2kbx+b2-m2=0,結合韋達定理,xM=■=■,yM=kxM+b=■.直線OM的斜率可表示為-■,所以兩直線的斜率之積kOM·k=-■·k=-9,即直線OM的斜率與直線l的斜率之積為定值-9.
第(2)問分析四邊形OAPB能否為平行四邊形,其中點A和B為對頂點,而點P為OM延長線與橢圓的交點,分析時需要以平行四邊形的判定定理為依托,構建與點坐標相關的條件,然后分析條件是否成立,即采用“先假設,后論證”的思路.
分析平行四邊形的判定定理,可將定理歸為三類:一是僅與平行相關;二是涉及線平行和相等;三是對角線相互平分.考慮到解析幾何的問題特點,從點坐標角度來看分析四邊形的對角線是否相互平分更為容易. 因此可以按照如下思路求解:設出點P的坐標,根據“對角線相互平分的四邊形為平行四邊形”的判定定理可得與坐標相關的條件,然后聯立直線OM與橢圓C的方程,分析是否存在這樣的直線OM.
設點P的坐標為(xP,yP),若四邊形OAPB為平行四邊形,則AM=BM,PM=OM,其中點M為AB的中點,則只需求證點M為線段OP的中點即可.轉化為坐標則必須滿足xP=2xM. 聯立直線OM與橢圓C的方程:y=-■x,9x2+y2=m2,可解得xP=■. 將點■,m代入直線l的方程中,可解得b=■,結合(1)問可知xM=■=■,于是有■=■,從而可解得k1=4-■,k2=4+■.所以當直線l的斜率為4-■或4+■時,四邊形OAPB為平行四邊形.
解后反思
上述是以橢圓與直線相交為背景的解析幾何綜合題,問題分為兩問,求證斜率之積是否為定值、探究四邊形是否為平行四邊形. 完成思路突破后還需引導學生對其進行反思,總結解題突破口,構建思維導圖,形成系統的解題思路.
1. 挖掘問題缺口
兩問均是解析幾何常見的問題類型:定值問題和存在性問題. 問題以橢圓的方程為背景,求證兩直線的斜率為定值,需要依托點的坐標來構建直線的斜率,故解題的突破口是聯立直線與橢圓的方程,根據韋達定理來轉化出點M的坐標;而第(2)問求證四邊形為平行四邊形,其判定定理有很多,難點在于如何選用定理及簡捷提取成立條件,故解題的突破口是根據解析幾何問題的點坐標特性,從對角線平分中提取與坐標相關的條件.
2. 構建思維導圖
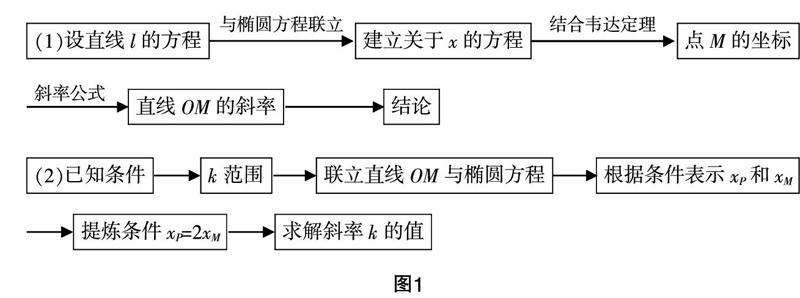
從解題過程來看,運算過程較為簡潔,實則是問題分析充分到位,所構思路清晰,取得了直切主體的效果. 因此求解解析幾何問題時需要重點關注解題思路的構建,在解題教學中需要構建相應的思維導圖,利用圖式來引導學生思考問題,培養學生正確的解題思維.以上述考題的兩問為例,可以構建圖1所示的思維導圖.
教學微設計
解題教學中需要利用考題的代表性來指導學生掌握問題的分析方法,形成相應的解題思維,除了可以構建相應的思維導圖外,還可以基于考題進行教學微設計. 微設計的過程中需要對考題進行拆解,逐步引導學生思考,掌握合理的分析步驟.
環節(一)——審題讀題,信息處理
已知橢圓C的解析式為9x2+y2=m2(m>0),直線l不經過原點O,且不與坐標軸相平行,設直線l與橢圓C相交于點A和B,點M為線段AB的中點,根據題干信息來繪制草圖.
意圖與分析:該環節主要是引導學生來提取題干中的關鍵信息,根據信息來繪制草圖,充分理解題干的信息條件,也是為后續數形結合輔助思考打下基礎,這也是解析幾何問題常用的解析策略.
環節(二)——拾級而上,引導審問
設直線l的方程為y=kx+b(k和b均不為0),點A(x1,y1),B(x2,y2),試回答下列問題.

