高中生數學抽象素養培養的實踐研究
胡昌亮
[摘? 要] 抽象素養的第二和第三水平的高低直接影響著學生解決中檔題和綜合難題的能力. 筆者以自己的課堂教學實踐為背景,芻議了抽象素養培養的兩個途徑:層第性培養學生的抽象素養;利用課堂的生成性發散思維提升抽象素養.
[關鍵詞] 抽象素養;層第性培養;發散思維;閱讀素養
新的課程標準中,描述了高中數學核心素養的六個主要方面,即數學抽象、邏輯推理、數學建模、運算能力、直觀想象和數據分析,并從概念的界定,及其在數學與生活中的作用和意義方面進行了描述. 在素養之一的數學抽象中,便指出數學抽象是指舍去事物的一切物理屬性,得到數學研究對象的思維過程. 給出數學抽象的作用是使得數學成為高度概括、表達準確、結論一般、有序多級的系統.
在現實教學過程中,學生可以根據熟悉的情境直接抽象出數學問題,形成解決問題的思路和方法,可是遇到稍微難的題目,就會出現抽象障礙,這類題目,即新課標中關于抽象素養的三個水平維度的第二和第三水平:聯系和創造. 如何高效地培養學生的抽象素養是一線教師需要深究的.
層第性培養學生的數學抽象素養
學生的學習不是一蹴而就的,這需要我們教師在教學過程中循序漸進地引導,形成系統性的解題經驗. 下面筆者以導數與函數單調性的關系為背景,從4個水平維度闡述如何層第性培養學生的抽象思維品質.
水平1(導函數可解可作圖型):函數f(x)=(x2+2x)ex(x∈R)的單調遞減區間為__________.
評價:這是較簡單的一類函數單調性求解題型,求導后解不等式即可. 但直接解不等式得出單調區間畢竟是非區分題,對于壓軸題,并不能直接解決. 實際上不等式的解集反映在圖像之上,即為x軸的上方或下方部分對應的自變量范圍,所以只要能作出導函數中符號可變部分的大致圖像,如本題中的y=x2+4x+2,再結合零點,就可求出單調區間. 這樣以形助數,抽象思維與形象思維相結合,可以為后面的深度學習打下扎實的基礎.
水平2(導函數可猜零點型):函數f(x)=ex+■x2-(2+ln2)x的增區間為____.
評價:函數求導后,由于不會求導函數的零點,學生可能解不出不等式,但導函數單調性仍可判斷,故可引導學生猜出零點. 由于導函數的表達式出現了ex及ln2,根據指數函數與對數函數的關系可猜零點為x=ln2,作出草圖,數形結合即可求出單調性.
水平3(導函數零點可設型):函數f(x)=e2x-alnx. 證明:當a>0時, f(x)≥2a+aln■.
評價:求導后導函數的零點不可求或者不可猜,但能判斷其零點存在,考慮設出導函數的零點,并得到函數的最小值,則有f(x)≥f(x0)=e■-alnx0. 教師之后引導學生利用2e■-■=0將e■-alnx0化簡為f(x0)=e■-alnx0=2ax0+■+aln■,再利用基本不等式即可得出結果. 經此,學生后面遇到類似問題會有兩方面的意識:一是零點不能求仍然可以設出來;二是可以利用零點滿足的方程,將最值表達式中的指數、對數式子化簡為不含指數、對數背景的表達式.
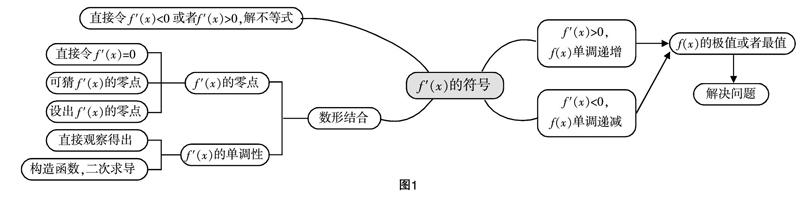
水平4(二次求導型):若函數f(x)=■,0 評價:本題只要能判斷出函數f(x)在(0,π)內的單調性即可. 學生求導后,亦可猜出零點,但由于f ′(x)的單調性無法判斷,這是本題的思維障礙點. 此時引導學生為判斷f′(x)的單調性,構造函數g(x)=xcosx-sinx并求導,可判斷g′(x)為負,即f ′(x)單調遞減;由f′(0)=0,可知f ′(x)在(0,π)上恒負,所以函數f(x)在(0,π)內遞減,即a>b. 圖1是4個水平層次的思維導圖,由淺入深螺旋遞進,學生層第性解決每個水平上的思維障礙點,獲取知識的本質,提高自身的抽象素養. 有效利用課堂上學生的生成性發散思維,因勢利導解決問題 眾多學者所寫的關于發散思維的論文比較集中在“一題多解”上,筆者在此不再贅述,此處筆者想談一下怎樣利用課堂上自然生成的發散思維來達到提升抽象素養的目的. 在函數不等式問題中,經常需要構造函數,由“導”尋“源”,解決問題. 比如下面一道選擇題: (單選)已知函數f(x)是定義在(0,+∞)上的非負可導函數,且滿足xf′(x)+f(x)≤0,對于任意正數a,b,若a A. af(a)≤f(b) B. bf(b)≤f(a) C. af(b)≤bf(a) D. bf(a)≤af(b) 由“導”尋“源”,學生構造函數g(x)=xf(x),則g′(x)=f(x)+xf′(x)≤0,所以g(x)=xf(x)為(0,+∞)上的減函數. 因為a 學生課堂生成性的發散思維有多個來源,上面顯然就是因為學生思維的起點不同而出現的解題方式. 作為教師,應該利用好課堂上寶貴的生成性資源,理清思路,肯定學生,課堂氛圍民主,學習才能高效,抽象素養也才能隨之得到培養. 學生的抽象素養并不是依靠口頭的傳授,更不是通過題海戰術獲得,它需要我們在平時的教學中,層第性地去啟發,同時抓住課堂上的思維閃光點作為我們的教學素材. 最后,希望筆者的一點點教學實踐可以給廣大教師帶去一些思考.

