基于分段設計的動力翼傘軌跡規劃

朱二琳 高海濤 趙俊杰

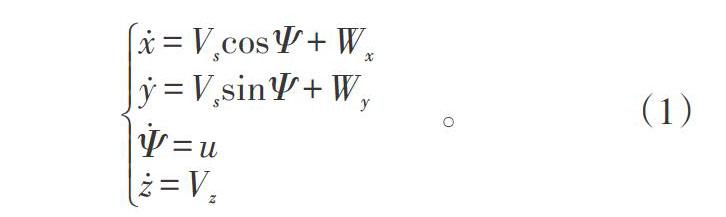
摘? ? 要：針對動力翼傘的飛行特點，對飛行及回收過程的軌跡規劃問題進行研究。根據實際飛行工況，在傳統翼傘軌跡規劃中，加入了動力翼傘的任務執行階段。根據各階段的幾何關系，將軌跡規劃問題轉換為幾何參數的尋優問題。以動力翼傘的回收精度最優作為優化目標，采用量子遺傳算法對目標函數進行尋優計算，得出各段軌跡的幾何參數。仿真分析驗證了該設計方法的可行性和有效性。

關鍵詞：動力翼傘;軌跡規劃;分段設計;量子遺傳算法

中圖分類號：V455.2? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? 文章編號：2095-7394（2020）04-0028-08

動力翼傘作為一類新型的柔性飛行器，在傳統翼傘系統的基礎上加入了動力推進裝置，與傳統翼傘相比，除了能夠完成滑翔和轉彎運動，它還能在空中維持高度、甚至爬升[1]。憑借這些優良的飛行特性，目前動力翼傘在軍事偵察、農業播撒、廣告宣傳等領域得到了廣泛的應用。

傳統翼傘的歸航方法一般分為三種[2-6]：簡單歸航法（包括徑向歸航和帶盲區的錐形歸航）、最優控制歸航法、分段歸航法。20世紀90年代以來，分段歸航法以其方法簡單、易于實現的特點被廣泛地應用于實際工程。根據翼傘自身的飛行特性，將翼傘從投放到著陸的整個過程分為幾個階段，再根據各個階段的特點，進行分段軌跡的設計，這就是工程中普遍應用的翼傘分段歸航法。熊菁對傳統翼傘的分段歸航做了詳細介紹，采用改進的遺傳算法對分段軌跡進行優化[7]。張興會考慮了能量最優，提出了基于能量約束的分段軌跡優化方法，既保證了著陸精度又節省了能量消耗[8]。然而，目前對于動力翼傘的軌跡規劃問題還沒見到相關的研究文獻。

近年來，隨著航空航天科技的發展，對翼傘自主歸航的要求越來越高，而飛行前的軌跡規劃有利于能耗的降低及回收，特別是對于動力翼傘，其所執行的任務并不僅限于物資的空投和回收，所以有效的軌跡規劃顯得尤為重要。本文采用量子遺傳算法研究了基于分段設計的動力翼傘的軌跡規劃問題，并通過仿真對所提算法的可行性進行了驗證。

1? ?動力翼傘質點模型

對于飛行器的軌跡規劃問題，復雜的動力學模型將增加運算的復雜度，會影響軌跡的準確性[9]。本文采用較為簡單的3自由度質點模型，在建模之前，先做如下幾點基本假設：

（1）在飛行過程中，將動力翼傘看作一個質點，不考慮姿態的變化，水平速度保持不變;

（2）在任務執行階段，動力翼傘等高飛行，垂直速度為零，在其他階段，垂直速度為定值;

（3）只考慮水平面的風場，且風場信息已知。

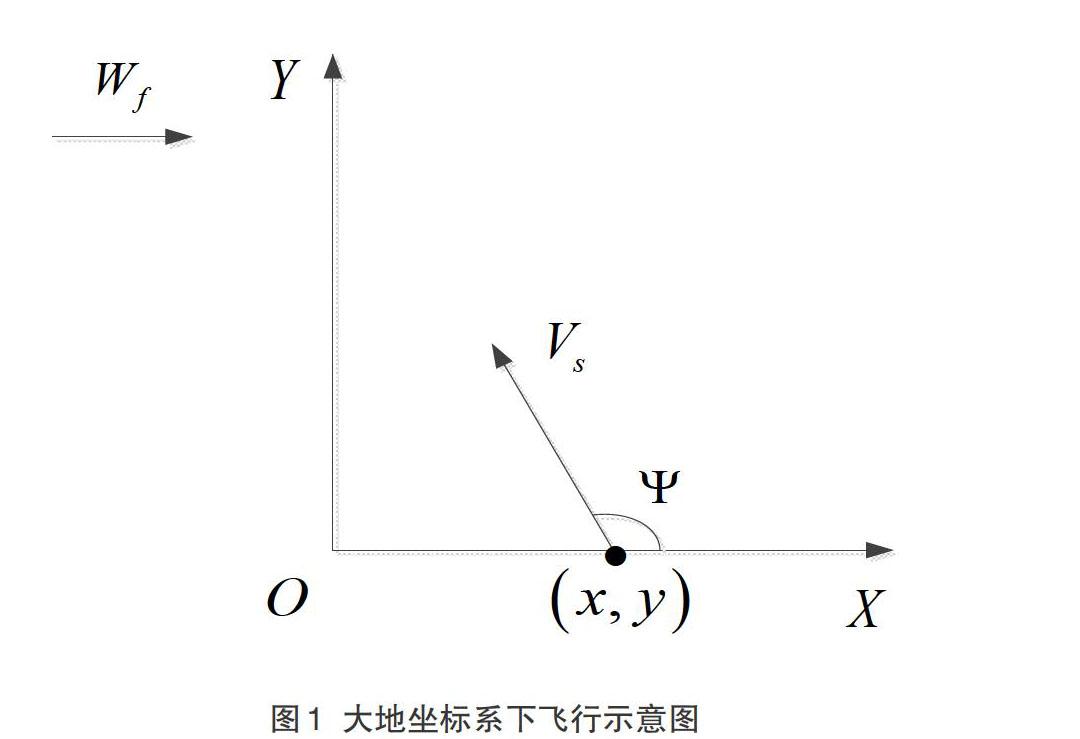
如圖1所示為動力翼傘水平面的飛行示意圖，大地坐標系原點為著陸的目標點，X軸的方向同風場方向保持一致，Z軸方向垂直向下，Y軸同X軸、Z軸共同構成右手坐標系。

根據飛行示意圖，可將動力翼傘模型簡化成如下形式：

其中：（[x y z]）代表動力翼傘在大地坐標系下的位置;[Vs]和[Vz]分別代表動力翼傘的水平速度和垂直速度（在任務執行階段[Vz=0]）;[Ψ]代表水平飛行方向同大地坐標系X軸之間的夾角;[Ψ]代表轉彎角速度;[u]代表傘繩控制量（同轉彎角速度之間存在對應關系）;[W]代表水平風場信息。

對于動力翼傘而言，任務執行段的軌跡應是固定不變的，不能隨風產生漂移，所以動力翼傘的軌跡規劃問題不能在風坐標系下進行討論。本文的研究基于上述的大地坐標系，在軌跡規劃過程中，不考慮風的因素。

2? ? 動力翼傘分段軌跡設計

2.1? ?分段策略

傳統翼傘的歸航軌跡可大致分為三個階段[7]：向心段，從翼傘初始投放點到著陸區域;能量控制段，在著陸區上空盤旋削高直到滿足一定高度條件;著陸段，尋找逆風方向、滑翔，最后進行雀降。對于動力翼傘的軌跡規劃問題，是在傳統翼傘的歸航過程中加入特定的任務執行段，當任務執行完畢后再進行歸航。動力翼傘目前主要應用于特定的工況，通常將動力翼傘的任務執行階段設定為擁有固定圓心和半徑的圓。

動力翼傘水平方向運動只能通過單拉傘繩和雙拉傘繩來進行控制，所以動力翼傘水平面的軌跡可以看作是直線和圓弧的組合。圖2為動力翼傘分段軌跡的結構示意圖。

如圖2所示，A點是動力翼傘的初始點，O點是著陸的目標點，BC段和DE段是動力翼傘的向心段，分別對應任務執行區域和著陸區域。以[O3]點為原點、[RTP]為半徑的圓形軌跡為動力翼傘的任務執行階段，此階段動力翼傘高度保持不變。FG段為能量控制段，此階段動力翼傘盤旋削高。HO段為著陸階段。AB、CD、EF、GH段為各階段的過渡階段，動力翼傘以最小的轉彎半徑轉彎飛行。[βii=1，…，5]代表最小半徑圓弧對應的圓心角弧度。根據各段軌跡的幾何關系，動力翼傘軌跡規劃的關鍵就是確定任務執行段的進入點D和能量消耗段的進入點F。R代表圓弧的半徑，[θ]代表進入點和對應階段圓的原點連線同大地坐標系X軸正向的夾角。下標TP代表任務執行段進入點，EP則代表能量控制段的進入點。[RTP]根據實際工況可事先設定，所以待優化的軌跡參數為[θTP，REP，θEP]。

2.2? 各段軌跡的計算

[n1，n2=1]代表動力翼傘逆時針轉彎，[n1，n2=-1]代表動力翼傘順時針轉彎。[x0y0z0]代表初始位置，[α0]代表初始飛行方向，[Rmin]代表過渡段最小轉彎半徑。

2.3 目標函數

動力翼傘歸航同傳統翼傘類似，需要保證以下兩點：（1）著陸點距目標點誤差最小;（2）著陸方向為風向的反方向。在分段軌跡設計中已經考慮了逆風對準，所以動力翼傘軌跡規劃的目標函數選擇為從初始點到目標點飛行的水平面軌跡同定滑翔比條件下初始高度對應的水平距離之間偏差的絕對值。由于動力翼傘在任務執行段飛行高度保持不變，因此，在目標函數中這一階段的水平面軌跡可忽略。

目標函數如下式所示： [J=Rmin?β1+β2+β3+β5+REP?β4+BC+DE+REP-2Rmin?REP-f?z0]? 。? （11）

其中：[f]代表滑翔比，[f=Vs/Vz]，[z0]代表初始高度。分段軌跡的參數變量為[θTP，REP，θEP]，以下通過參數尋優的方法對軌跡規劃問題進行求解。

3? ?量子遺傳算法

量子遺傳算法（Quantum genetic algorithm，QGA）[10-12]是量子計算和遺傳算法相結合的產物。染色體在編碼過程當中，引入量子的概率幅表示方法，從而使每個染色體能夠表示多個狀態的疊加。通過量子旋轉門策略對染色體進行更新，可達到對目標函數的最優求解，因此，只要是遺傳算法能夠求解的優化問題，都可以用量子遺傳算法來解決。

對于上文描述的動力翼傘分段軌跡優化問題，目標函數如式（11）所示，這是一個標準的多變量參數尋優問題，很適合用量子遺傳算法來進行求解計算。根據上述問題描述，優化的參數變量為[θTP，REP，θEP]。轉彎方向根據初始點位置的不同可有不同的組合方式，在優化之前進行確定，針對不同的[n1，n2]值分別對目標函數進行量子遺傳算法的求解，并選取最優的解。

量子遺傳算法對分段軌跡參數尋優的具體步驟如下：

（1）采用小生境協同進化策略，對種群[Q（g0）]進行初始化;

（2）測量種群[Q（g0）]中每個染色體，可得二進制編碼;

（3）計算目標函數，對種群[Q（g0）]中所有個體逐個進行適應度的評價;

（4）選擇適應度最優的個體，并保存相應的適應度值;

（5）判斷是否滿足結束條件，如果是，轉向步驟（11）;

（6）測量種群[Q（g）]中每個染色體，得到二進制編碼;

（7）對種群[Q（g）]中所有個體逐個進行適應度的評價;

（8）通過量子旋轉門對種群[Q（g）]進行更新，得到下一代的種群[Q（g+1）];

（9）選擇適應度最優的個體，并保存相應的適應度值;

（10）轉向步驟（5）;

（11）將優化所得的最優參數[θTP，REP，θEP]代入相應的公式，得到各段的軌跡;

（12）結束。

4? ? 仿真分析

以動力翼傘的質點模型為基礎，本節對所提出的分段軌跡優化方法進行仿真驗證。動力翼傘的水平速度[Vs=13.8 m/s]，無動力驅動時垂直速度[Vz=4.6 m/s]，滑翔比 [f]=3。動力翼傘任務執行段軌跡圓心坐標為（1 000，0）[m]，半徑[RTP=500 m]，[Rmin=100 m]。約束條件[REP∈230500 m，][θTP，θEP∈-ππ]，[βi（i=1，…，5）∈0π]。

（1）動力翼傘初始位置：[x0 y0 z0=1 850 600 1 380 m]，初始飛行方向：[Ψ0=-π/3]。

通過量子遺傳算法的求解計算，所得最優參數：[θTP=-2.25]，[REP=300 m]，[θEP=2.34]。

仿真結果如圖3所示。

由圖3（a）動力翼傘的水平面飛行軌跡不難看出：動力翼傘首先由初始點飛翔至任務區域，由任務段進入點（[θTP=-2.25]）開始任務執行階段;然后動力翼傘開始歸航，進行回收，由能量控制段進入點（[REP=300 m]，[θEP=2.34]）進行盤旋削高;最后，逆風對準，滑翔著陸。整個過程是滿足動力翼傘飛行和歸航特點的。由圖3（b）的側向面軌跡圖可以看出：當動力翼傘著陸時，恰好達到目標點，著陸誤差為0.41 m。如圖3（d）所示為左右傘繩的控制量[u]，控制量的定義見公式（1），正值代表右轉，負值代表左轉，分段軌跡的控制曲線為分段的直線。通過電機帶動下拉傘繩，能夠避免執行機構頻繁的動作，在降低能耗的同時也有利于系統的穩定性，從而更加切合實際的工程應用。

（2）動力翼傘初始位置：[x0 y0 z0=200 600 1 380 m]，初始飛行方向：[Ψ0=-2π/3]。

通過量子遺傳算法的求解計算，所得最優參數：[θTP=-2.15]，[REP=302.3 m]，[θEP=1.44]。

仿真結果如圖4所示。

當動力翼傘初始位置發生變化，仍然能規劃出一條合理的軌跡，最終的著陸精度為0.38[m] ，說明了分段軌跡設計方法的魯棒性。

5? ? 結論

本文主要對動力翼傘的分段軌跡規劃相關問題進行了研究。在傳統翼傘分段歸航過程中，加入了動力翼傘的任務執行階段，當動力翼傘完成任務執行階段之后，進行歸航回收階段。根據各分段軌跡的幾何關系，將軌跡規劃問題轉換成參數尋優問題;采用量子遺傳算法對分段軌跡的目標函數進行求解計算，得到設計參數的最優值，將最優參數代入計算出各分段軌跡，獲得動力翼傘總的飛行軌跡。

上述研究中，動力翼傘的垂直下降速度在任務執行階段為0，在其他階段為固定不變的值，后續的研究中還會將動力翼傘垂直速度的變化情況考慮進去。此外，目標函數主要基于著陸誤差而建立，并沒有考慮控制能量的約束，但在實際飛行過程中，動力翼傘攜帶的能量是有限的，對于這一問題也將在后續的研究中予以解決。

參考文獻：

[1] ZHU E L，SUN Q L，TAN P L，et al. Modeling of powered parafoil based on Kirchhoff motion equation[J]. Nonlinear Dynamics， 2015，79（1）：617-629.

[2] PEARSON A E， WEI K C，Koopersmith R M. Terminal control of a gliding parachute in a nonuniform wind[J]. AIAA Journal，1977，15（7）：916-922.

[3] 熊菁，秦子增，文紅武.翼傘系統歸航的最優控制[J].航天控制，2004，22（6）：32-36.

[4] 焦亮，孫青林，亢曉峰.基于混沌粒子群優化算法的翼傘系統軌跡規劃[J].復雜系統與復雜性科學，2012，9（1）：47-54.

[5] ZHANG L M，GAO H T，CHEN Z Q，et al. Multi-objective global optimal parafoil homing trajectory optimization via Gauss pseudospectral method[J]. Nonlinear Dynamics，2013，72（1-2）：1-8.

[6] TAO J，SUN Q L，ZHU E L，et al. Quantum genetic algorithm based homing trajectory planning of parafoil system[C]. Hangzhou：Proceedings of the 34th Chinese Control Conference，2015：2523-2528.

[7] 熊菁. 翼傘系統動力學與歸航方案研究[D]. 長沙：國防科技大學，2005.

[8] 張興會，朱二琳. 基于能量約束的翼傘系統分段歸航設計與仿真[J]. 航天控制，2011，29（5）：43-47.

[9] SAUNDERS D，ALLEN G，GAGE P，et al. Crew transfer vehicle trajectory optimization[C]. Anaheim：35th AIAA Thermophysics Conference，2001：2001-2885.

[10] YANG J A，LI B，ZHUANG Z Q. Research of quantum genetic algorithm and its application in blind source separation[J]. Journal of Electronics，2003，20（1）：62-68.

[11] 傅德勝，張蓉. 一種改進的量子遺傳算法研究[J]. 計算機仿真，2013，30（12）：321-325.

[12] 劉振，彭軍，劉勇.小生境分布估計量子遺傳算法及其仿真分析[J]. 計算機工程與科學，2016，38（1）：89-94.

責任編輯? ? 盛? ? 艷