新工科背景下的應用型本科工程教育中計算思維培養

吳志澤 王艷

摘要：計算思維是高等工程教育的關鍵。為應對以人工智能為核心的新一輪科技革命，“新工科”建設在我國全面啟動，為應用型高等工程教育中的計算思維培養提出了新的挑戰。本論文從回歸計算思維本質出發，探討新工科背景下的應用型本科工程教育中計算思維培養問題，提出從傳統的計算思維到人工智能時代的計算思維的觀念糾正，并以機器學習中的計算思維進行實例分析，最后提出應用型本科工程教育中計算思維培養建議。

關鍵詞：應用型;工程教育;計算思維

中圖分類號： G424 ? ? ? ?文獻標識碼：A

文章編號：1009-3044（2020）17-0101-03

1 前言

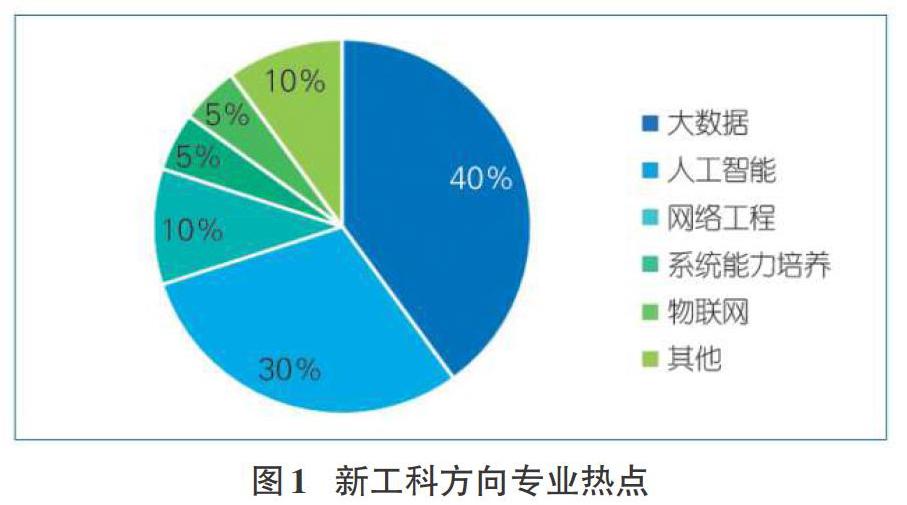
以人工智能為核心的新一輪科技革命正在孕育興起，信息技術日益成為創新驅動發展的先導力量。以新技術、新業態、新產業、新模式為特點的新經濟蓬勃發展，分享經濟、大數據、虛擬現實、人工智能等新興領域風起云涌，為應用型本科教育帶來了新機遇、新挑戰[1]。

應用型高等工程教育在我國高等教育中占有重要的地位，培養高素質應用型工程科技人才是支撐產業轉型升級、實施國家重大發展戰略的重要保障[2]。目前，我國已建成了世界上最大規模的工程教育體系，工科本科專業全國布點18000多個，在校生500多萬人，形成了4200多萬人的工程科技人才隊伍。2016年6月，我國成為《華盛頓協議》組織的正式成員①，標志著中國工程教育質量認證體系實現了國際實質等效，為進一步深化工程教育改革奠定了堅實基礎，提供了良好契機[3]。

為主動應對新一輪科技革命與產業變革，教育部2017年啟動了“新工科”建設，從“復旦共識”“天大行動”到“北京指南”，提出了以實施“卓越工程師教育培養計劃2.0 版”為抓手，把握工科的新要求，加快建設發展新興工科的號召。新工科建設“三部曲”推動了我國工程教育改革持續走向深入，新工科已經成為高教戰線的廣泛共識和積極行動。

2019年1月，高等教育出版社出版了由“中國計算機教育20人論壇”發布的《計算機教育與可持續競爭力》[4]一書。融合國際最新的計算機教育領域觀點，我國的計算機教育專家們站在了更為全面且更加符合中國國情的角度，闡述了可持續競爭力（或稱勝任力）的概念，以及如何培養可持續競爭力。中國學者創新地提出了敏捷教學的概念與內涵[7]，并再次重申了計算思維的重要性和特征。

計算思維與核心課程、系統能力、產教融合、國際化能力是計算機教育（敏捷教學）的五大關鍵。本論文從回歸計算思維本質出發，探討新工科背景下的應用型本科工程教育中計算思維培養問題，提出從傳統的計算思維到人工智能時代的計算思維的觀念糾正，并以機器學習中的計算思維進行實例分析，最后提出應用型本科工程教育中計算思維培養建議。

2 計算思維定義

計算思維的概念在20 世紀70 年代末被提出，并在20 世紀80 年代成文，然后開始了一定范圍內的探討（如西蒙·派珀特博士（Seymour Papert） 在1980 年的Mindstorms： Children， Computers， and Powerful Ideas一書和1996 年的“An Exploration in the Space of Mathematics Educations”論文）[7]。同一時期，諾貝爾物理學獎獲得者Wilson 提出計算是所有科學的研究范式之一，區別于理論和實驗，所有的學科都面臨算法化的“巨大挑戰”。所有涉及自然和社會現象的研究都需要借助計算，使用計算模型做出新發現和推進學科發展。Wilson的工作和對于計算方法的大力推薦，激發了人們對于計算科學的認識和重視。

然而，直到2006 年3 月，卡耐基梅隆大學的周以真（Jeannette Wing） 教授在CACM 上發表文章[6]，才將計算思維的概念重新帶入了大家的視線并引起了各界關注。她認為計算思維是運用計算機科學的基礎概念進行問題求解、系統設計以及人類行為理解等涵蓋計算機科學之廣度的一系列思維活動。她同時提出了計算思維的特征及方法，使計算思維在世界范圍內得到推廣。周教授的這篇文章以及她后續作為美國國家科學基金會（NSF） 計算機信息科學與工程學部（Computer and Information Science and Engineering， CISE） 助理主任客觀上推動了計算思維的NSF 基金立項，并且將計算學科的概念、方法、工具和技術融入中小學和大學本科教育中。

我國非數值并行算法研究的學科帶頭人陳國良院士，在2011年提出計算思維并不是僅僅為計算機編程，而是在多個層次上抽象的和工程的思維，是一種以有序編碼、機械執行、和有效可行方式解決問題的模式。計算思維是一項根本能力，是每一個人在現代社會中必須掌握的。

例如，著名學者Alfred Aho在2011年提出計算思維是一個思想過程，涉及描述問題使得它們的解決能夠通過計算步驟和算法，能夠被信息處理裝置有效實現，計算模型是核心概念。

美國國際計算機教師協會（ISTE）（2011）：計算思維是具有以下特征的問題解決過程：以一種能夠使用計算機和其他工具幫助解決問題的方式制定規劃;合理組織和分析數據;通過模型和模擬等抽象的表示數據;通過算法思維（一系列有序步驟）實現解決方案自動化;確定、分析和實施可能的解決方案，以實現最有效的過程和資源組合;將問題解決過程推廣轉化到其他各種各樣的問題。

計算思維源于各個學科對于計算的需求和依賴。2017年，Peter J.Denning指出：計算思維是從不同的科學領域發育和成長的，并不只是從計算機科學中輸入的，事實上，計算機科學是逐步地參加到這個思維的變革中來。一場安靜但是深刻的已經在所有的科學領域發生，計算賦能的革命通過信息技術帶來了各種類型的新的發現。

總之：計算思維是計算機科學的本質思維模式，是區別于物理學和數學的核心;計算思維是以計算為特征的認知世界和解決問題的基本思想;計算思維的核心是計算模型。

3 ?計算機與非計算機計算思維培養

計算思維是種以物質為本到以信息為本的思維轉變。計算思維從信息運動和結構的角度重新定義經濟活動和社會結構。例如電子政務、數字媒體、智慧城市、網絡安全等，都是在信息觀和算法觀下的對于自然、社會乃至人類自身的重新認識。計算思維是從數據認知問題和解釋問題的新角度和新模式，是不同于傳統地從一般原理到具體實現的套路。而是從具體的事例到一般性規律的認知。

人工智能發展為計算思維提出了新的挑戰。傳統的算法設計是從一般到具體的求解問題的思路（即所謂具化）。而人工智能中面臨著另一類算法，從具體到一般的求解問題的思路（即所謂泛化）。對于前者的算法，它的設計、評價和分析都具備了較為成熟的理論，對于后者，數學意義上的精確性基本是不存在的，必須容許某種不精確性和不確定性，對于這類算法的設計原則，評價標準和性能比較都需要有新的思路。

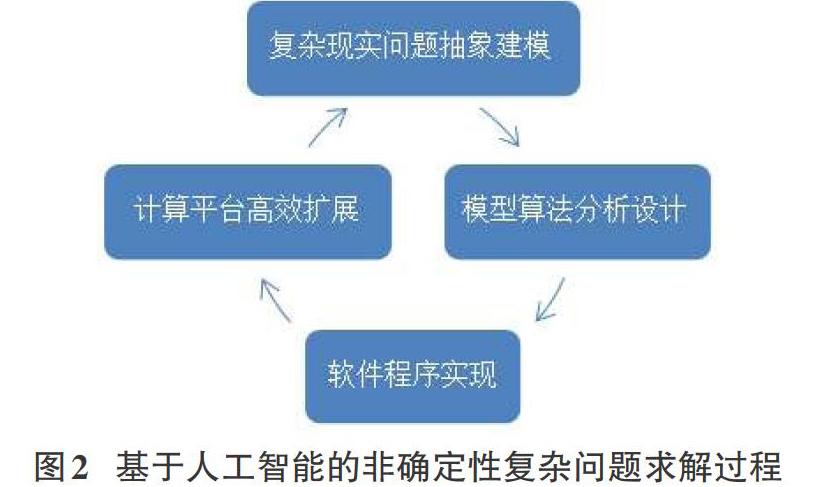
人工智能所要解決的是非確定性復雜問題，其求解過程如圖2所示。這一過程對應用型高等工程專業人才在數理理論與計算思維方面提出了更高的要求：需要深厚的數理理論基礎;扎實的計算與系統思維。人工智能時代的計算思維的關注點包括：可計算和計算復雜性、關注對象的信息特征、從數據中歸納原理、信息處理的算法設計、不同過程和對象間的可靠信息傳遞、可靠和可信的計算系統構建、復雜系統和智能系統的性能評價、多個自主智能實體間的有效配合和時序控制、機器知識與人類知識之間的關聯、信息與知識的有效表示、存儲和檢索等。

限于編程的計算思維容易忽略計算思維的本質。計算思維既作為基本的科學對象，同時也具有學科的橫向價值，從不同學科領域萌發的計算技術和方法，經過計算機學科的精雕細琢以后，又為解決其他學科的問題提供了新的思想和方法。“計算機科學家”的思維方式并不優于其他方式，只是提供了一種描述現實的新的和有用的概念范型。

計算思維的第一功能是提出問題和設計解決問題的模型，即如何實現計算過程，而不僅是具體實施計算過程。將計算思維理解為設計和實現“step by step”的編程過程，忽略了對于自然世界和人類行為的整體理解和科學建模（計算模型）所具有得更為深遠和本質的內容。從設計思想理解程序比熟悉它的具體語句更重要，讓學生對電腦編程，而不是電腦對學生編程（固化了思維模式）。

4 機器學習中的計算思維舉例

4.1 可學習性與可判定性

推薦系統：S個團體Zi，每個團體的成員有相似的消費習慣;根據當前的消費情況，向相應的團隊中每個人進行推薦（任務）;已知當前的消費實例（條件）。

學習：根據當前消費狀態數據庫D，進行學習訓練，建立推薦模型，向所有潛在消費者進行廣告投放。

學習算法與傳統算法的思維區別在于：傳統算法是自上而下的，由一般到個體，對于一類問題整體進行設計，對于其中每一個實例（instance），該算法調整個別參數，其計算的結果是精確的，對于近似計算，近似程度是一致的;學習算法是自下而上的，由個體到一般，通過具體的數據學習，實現對于一般情況的計算，其計算結果由兩個概率度量，一個是誤差的概率，一個是達到這個誤差的概率。

換言之，學習算法可能近似正確算法（PAC算法），通過少量實例的學習，獲得泛化的知識。模擬人類知識傳承、機器人控制、知識獲取、知識應用。因此對于算法的評價、實施以及設計原則，該兩類方法都是不同的。

對于任意的消費群體組合，若有足夠的歷史數據，是否可以學習出合理的推薦系統嗎？這就是可學習問題。答案是不確定的。那么，對于給定的任務，具體的數據庫，具體的消費群體組合，它的可學習性是可判定的嗎？這是個判定問題，答案是不能。

4.2復雜系統的線性化

聚類分析問題：對于復雜的數據集合，如何通過樣本的學習，獲取分類函數。要求快速而容錯的分類，即數學方法標準精確，分類誤差嚴格。例如PAC分類，以[1-δ]概率保證分類誤差不超過[ε]（容錯分類）。

針對聚類問題，數學思維會設計統一的算法出發，對于所有分類對象，采取統一的分類模型，達到整體一致的分類標準。標準的算法的復雜度為O（n2）， n是數據的個數。而計算思維會采取分而治之的方法，設計多個局部區域，每個局部區域采取線性分類模型，利用線性化方法實現復雜函數的計算。該類的標準方法是PAC。

該類方法不依賴總體數據量的聚類分析算法，當樣本數量[m≥23ε-1logδ-1]，以[1-δ]的概率保證誤差不超過[ε]的分類，與總體數量無關。圖3為聚類挑選代表元例子：（a）顯示的是原始點的分布，網格邊長為[u2]，共有175個點;（b）[ε-]網及聚類，[ε=0.02， ε*175=3.5，]少于3個點的區域可能被忽略。

5 結論

運用計算機科學的基礎概念進行問題求解、系統設計以及人類行為理解等涵蓋計算機科學之廣度的一系列思維活動。在信息社會中，最為活躍的創新領域都與信息技術聯系緊密，計算思維成為數學思維、工程思維的重要補充，是許多重大創新的核心要素。計算思維展示了不同的解決問題標準和方法。這些標準和方法在人工智能中有強烈的背景基礎和應用支持，掌握并習慣于新的方法有利于開發實用和有效的智能機器。對于應用型高等工程教育，計算思維是面向智能時代，優化計算機專業知識/能力培養體系的關鍵，也只有重構與優化計算機專業知識與能力體系，方能使得培養的計算機專業人才能夠適應新時代發展需求。

注釋：

①《華盛頓協議》于1989 年由來自美國、英國、加拿大、愛爾蘭、澳大利亞、新西蘭6 個國家的民間工程專業團體發起和簽署。該協議主要針對國際上本科工程學歷（一般為四年）資格互認，確認由簽約成員認證的工程學歷基本相同，并建議畢業于任一簽約成員認證的課程的人員均應被其他簽約國（地區）視為已獲得從事初級工程工作的學術資格。2013 年，我國加入《華盛頓協議》成為預備成員，2016 年成為《華盛頓協議》組織的正式成員。

參考文獻：

[1] 張龍，劉華：信息技術領域新工科建設與工程教育改革[J].計算機通訊，2019， 15（4）：26-28.

[2] 葉民，孔寒冰，張煒.新工科：從理念到行動[J].高等工程教育研究，2018（1）：24-31.

[3] 吳巖.新工科：高等工程教育的未來——對高等教育未來的戰略思考[J].高等工程教育研究，2018（6）：1-3.

[4] “計算機教育20人論壇”報告編寫組.計算機教育與可持續競爭力[M].北京：高等教育出版社，2019.

[5] 徐曉飛，李廉，戰德臣，等.新工科的新視角：面向可持續競爭力的敏捷教學體系[J].中國大學教學，2018（10）：44-49.

[6] Wing J M.Computational thinking[J].Communications of the ACM， 2006，49（3）：33.

[7] 張科， 張銘， 陳娟，等：計算機教育研究淺析——從ACM計算機科學教育大會看國內外計算機教育科研[J].計算機通訊，2019， 15（4）：16-25.

【通聯編輯：唐一東】