基于經驗視角 引之嘗試『自漁』
——《角的度量》教學實踐與思考（二）

王 笑

【教學內容】

蘇教版四年級上冊第79、80頁。

【教學過程】

一、基于經驗，操作中產生統一內需

1.回憶思辨。

師：老師手里有兩個角，∠A和∠B，（如下圖①②）你能一眼看出哪個角大嗎？

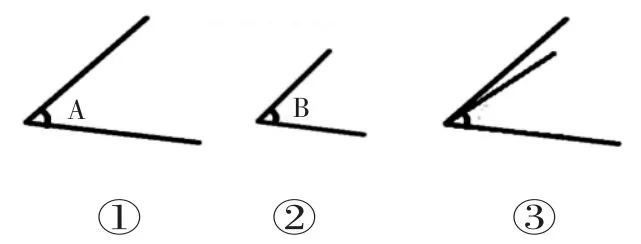
生：∠A 大，因為它的邊更長。

生：角的大小不是看邊的長短，這兩個角張開的大小是差不多的，需要重合起來比一比才能知道哪個角大。

師：請你為大家展示一下比角的方法好嗎？

生：將∠B 與∠A 的頂點和一條邊重合，看另一條邊，（如上圖③）∠A 大。

2.操作比劃。

師：∠A 到底有多大呢？我們可以借助學具籃中的角比一比。（如下圖：學具籃中有兩把三角尺及三個折成的小角。∠1 是60°、∠2 是30°、∠3 是22.5°）

（1）探究活動。

①拿一拿：從學具籃中拿出這些工具。

②比一比：同桌合作，用工具上的這些角去與∠A 比一比。

③說一說：同桌相互說一說∠A 有多大。

（2）交流反饋。

師：你們測量的結果是什么？

生：∠A 有一個∠1 那么大。

生：∠A 有兩個∠2 那么大。

生：∠A 大約有三個∠3 那么大。

師：同樣是測量∠A，結果為什么不同呢？

生：他們測量時用的工具不同。

生：我同意他的說法，但根據我們以往的學習經驗，我認為要知道∠A 的大小，最好能統一測量工具，這樣才能進行比較。

師：確實像這位同學所說，我們需要有一個統一的測量工具與方法，那就讓我們一起來研究“角的度量”。（板書揭題）

【思考：“影響學習的唯一最重要因素，就是學習者已經知道了什么，要探明并據此進行教學。”此環節，通過“回憶思辨”，復習了二年級學習的角的初步認識；通過“操作比劃”，感知∠A有一個∠1 那么大、有兩個∠2那么大、大約有三個∠3 那么大，此時教師引導并提出了一個關鍵問題——“同樣是測量∠A，結果為什么不同呢？”，由此引起認知沖突，產生了統一度量工具的內需。】

二、積累經驗，交流中明晰度量原理

1.初步感知量角器的產生過程。

師：知道要用什么工具度量角的大小嗎？

生：半圓形的量角器。

師：（邊問邊拆，如下圖①②）同學們，這是學具籃里的∠3，老師將它打開，你認識嗎？

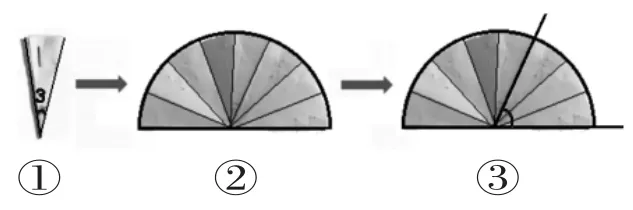
生：認識，它就是“量角器”！

師：是的，這是一把“簡易的量角器”，量角器其實就是由若干個角組成的。你能在量角器中找到角并說一說這個角有多大嗎？

生：（上臺指、說，如上圖③）這有一個角，它有三個∠3 那么大。

（隨后教師又請了三位學生到臺前在這個簡易量角器上找不同的角，并請同桌同學互相指、說）

【思考：初步感知量角器的產生過程，引導學生觀察并到黑板前指出大小不一樣的角，說一說這個角包含了幾個∠3。充分感知量角器里有很多不同的角，不同的角都是由若干個相同單位的角組成的。】

2.自主探究量角器的簡單構造。

師：那“精密的量角器”長什么樣呢？看！（課件出示量角器）觀察量角器，你看到了什么？

生：量角器上有很多刻度線，都指向量角器的中心。

生：量角器上面的數排成了兩圈。

師：是的，里面這圈刻度我們稱為內圈刻度，那外面這圈刻度叫什么呢？

生：外圈刻度。

師：量角器里藏了好多數學知識，請翻開教材第79 頁，帶著下面的思考，自學最后兩段話。

（1）明確思考。

①說一說：角的計量單位是什么？

②想一想：量角器上的1°角在哪里？量角器中有多少個1°角？

③找一找：從右邊起，找出0°、20°、90°、135°、180°刻度線；再從左邊起，找出0°、20°、90°、135°、180°刻度線。

（2）交流反饋。

生：度是角的計量單位，用符號“°”表示，1 度記作1°。（板書）

生：這兩條刻度線延長到中心就形成了1°角。

生：將這兩條刻度線延長到中心形成的角，度數也是1°。（如下圖）

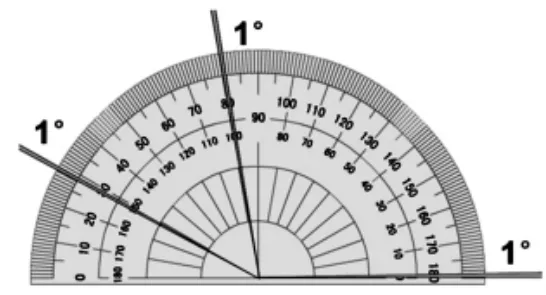
生：每兩個相鄰刻度間所對的角都是1°。

生：老師，我發現量角器中有180 個1°角。

師：你從哪里看出來的？

（學生到臺前指一指）

生：老師，我還知道這是左邊的0°刻度線、這是右邊的0°刻度線……（邊指邊說）

3.思維遷移讀整十度的角。

師：同學們了解了量角器，你會使用它嗎？那我們課前研究的這個∠A 到底有多少度呢？誰能用大屏上的量角器量一量？

生：（如下圖，學生邊擺邊說)將角的頂點與中心重合，一條邊與右邊0°刻度線重合，擺好后，我發現∠A 里有6 個10°角，所以∠A 是60°。

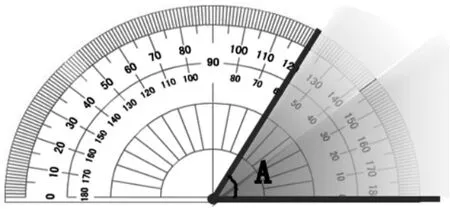
生：我認為角的一條邊與左邊0°刻度線重合也可以。

生：他們的方法都是可以的，但不用去數6 個10°角是60°，直接看它的另一條邊就可以了，另一條邊指著數字60，那就是60°。

生：我有疑問。另一條邊所在的地方，有60°和120°兩個度數，怎么確定是60°呢？

師：這個問題我覺得很有意思，誰能解答呢？

生：∠A 是個銳角，比直角小，所以不可能是120°。

生：其實∠A，它的起始邊與內圈0°刻度線重合，就讀內圈刻度60°。

生：我們只要看角的一條邊，與內圈的0°刻度線重合，就讀內圈刻度；與外圈的0°刻度線重合，就讀外圈刻度，所以讀出來都是60°。

【思考：學生的思維能力在經驗遷移中能得到很大的提升。在上一層次中，學生已經充分感知“量角器中不同的角都是由若干個相同單位的角組成的”，這一環節，學生在度量實物∠A 時，就很自然地說出“∠A 里有6 個10°的角，所以是60°”。學生走向臺前，大膽表達讀角的方法，生生互相補充，進行方法優化。】

4.認知提升讀非整十度的角。

師：（拿起實物∠B）同學們，看這個角，你也會像剛才一樣量一量它是多少度嗎？

生：這個角比40°大一些。（如下圖，學生上臺拿∠B 與課件中的量角器比對）

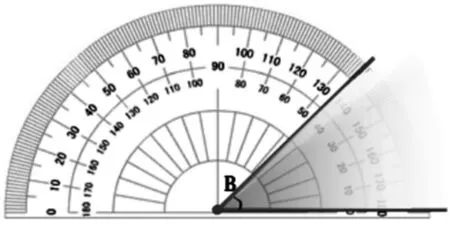
師：能準確地讀出∠B 的度數嗎？

生：（指著內圈，一度一度地數）40°、41°、42°、43°、44°、45°。∠B 是45°。

生：我要補充。我和他結論一樣，但我不用一度一度地數，5°刻度線稍微長一些，所以一眼就能看出是45°。

【思考：教育家波利亞提出“學習任何新知的最佳途徑是由學生自己去發現，因為這種發現理解最深，也最容易掌握內在的規律和聯系”。此環節，學生拿著∠A 去比對，比的過程中就學會了量角、讀角的方法；再拿著∠B去比對，發現不是整十度的角，于是自然產生“40°、41°、42°、43°、44°、45°”這樣一度一度地數的情況，這是學生解決認知沖突的需要，這樣的內在知識才會被理解得更深。】

三、發展經驗，活動中深探度量本質

1.嘗試操作。

師：度量畫在紙上的角，不能拿到量角器上去比怎么辦？（如下圖，教師出示75°的∠C 與130°的∠D）

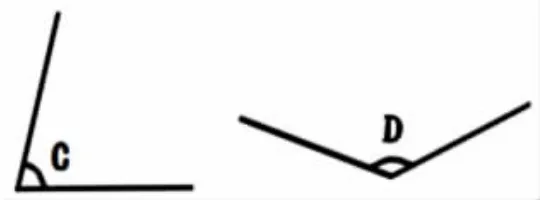
生：我們可以拿量角器到角上去比一比。

師：那行，請同學們動手試一試吧！

（學生嘗試操作，教師巡視，然后教師呈現學生動態操作過程的視頻）

2.資源呈現。

（交流呈現兩種動態視頻：第一種，度量∠C，完全正確；第二種，度量∠D，錯誤資源）

師：先請度量∠D 的學生代表說一說是怎么操作的，其他學生傾聽并補充。

生：量角器的中心和角的頂點重合，內圈的0°刻度線和一條邊重合，看另一條邊，所以∠C 是75°，有需要補充的嗎？

生：我同意你的觀點，另一條邊對應兩個刻度，分別是75°和105°，你應該強調一下，一條邊和內圈的0°刻度線重合，要讀內圈刻度，所以是75°。

師：認真傾聽是對別人的尊重，傾聽后的補充使得度量的方法更加完整。

師：再來看看第二個視頻，你有話要說嗎？

生：∠D 的一條邊不在水平方向，我們可以轉一下紙，使得一條邊在水平方向。

生：是的，我同意他的觀點。當然也可以將量角器稍微轉一轉，使得0°刻度線與∠D 的一條邊重合。

師：剛才量錯的同學，請再動手試一試！

【思考：“動手操作的過程，不僅是一個實踐的過程，更是嘗試、想象、推理和反思的過程。”兩種資源的捕捉，先呈現第一種，以生教生；然后呈現第二種，學生能及時發現自己的問題所在并糾正。動手操作，通過嘗試及反思，學生不僅學會了如何度量，還掌握了知識間的聯系，從拿著實物角到量角器上去比，發展到用量角器去量紙上的角。在此過程中，教師只是引導者，真正方法的獲得全部來自于學生自己經驗的發展。】

四、積累經驗，說明中發散度量思維

師：通過今天的學習，你有哪些收獲？我們是怎么探究的？

師：課后請你為量角器寫一份使用說明書。