讓概念在認知的生長點上“生發(fā)”
——《分數(shù)的初步認識》教學(xué)思考與實踐

汪玉瓊

【課前思考】

在數(shù)學(xué)課堂上，我們不僅要引領(lǐng)學(xué)生學(xué)習(xí)數(shù)學(xué)知識，更重要的是要發(fā)展學(xué)生的數(shù)學(xué)思維能力。所以教師在數(shù)學(xué)課堂中應(yīng)關(guān)注數(shù)學(xué)概念的本質(zhì)。所謂數(shù)學(xué)的本質(zhì)，就是指數(shù)學(xué)本身所固有的、決定數(shù)學(xué)學(xué)科性質(zhì)、面貌和發(fā)展的根本屬性。可以理解為，數(shù)學(xué)本質(zhì)就是具體數(shù)學(xué)內(nèi)容的本質(zhì)意義。因此，在教學(xué)中我們就得抓住對基本數(shù)學(xué)概念的理解，對數(shù)學(xué)思想方法的把握，追尋數(shù)學(xué)概念的根源，找到知識的生長點，突出數(shù)學(xué)的本質(zhì)。

在學(xué)習(xí)《分數(shù)的初步認識》這一課之前，學(xué)生接觸到的數(shù)只是自然數(shù)如0、1、2、3……，當遇到分數(shù)這樣的“新數(shù)”時，對學(xué)生來說是一個很強烈的認知沖擊。那么，怎樣讓分數(shù)的概念在學(xué)生的頭腦里誕生以及讓學(xué)生初步掌握分數(shù)的意義？將是我們本節(jié)課需要著重解決的問題。分數(shù)是數(shù)概念教學(xué)中的一部分，在引領(lǐng)學(xué)生認識分數(shù)前，我們必須了解分數(shù)的來源及意義，這樣才能幫助學(xué)生在頭腦中建立科學(xué)的數(shù)系。由此，我仔細查閱了相關(guān)資料，進行了認真分析研究。在義務(wù)教育數(shù)學(xué)課程中，數(shù)的概念包括自然數(shù)、整數(shù)、有理數(shù)等。數(shù)概念的形成過程是一個數(shù)概念外延多次擴張的過程。數(shù)系的擴充有兩條主要的途徑：一是元素添加。在自然數(shù)集合中添加“負整數(shù)”就得到了整數(shù)；在整數(shù)集合中添加“分數(shù)”就得到了有理數(shù)；在有理數(shù)集合中添加了“無限不循環(huán)小數(shù)”就得到了實數(shù)。二是等勢抽象（略）。分數(shù)的產(chǎn)生源于兩種需求：一是人們在分東西的時候，往往得不到整數(shù)的結(jié)果，需要對一個物體進行分割與分配，分割出來的表示整體中的“部分”無法用自然數(shù)來表示，這就需要有一種新的方式來表示這“部分”；二是在計算過程中，如3÷4 無法用自然數(shù)表示計算的結(jié)果，就需要有刻畫這類除法運算結(jié)構(gòu)的方式方法。找到了分數(shù)的本質(zhì)屬性以及知識的生長點，我嘗試進行了如下的教學(xué)：

【教學(xué)過程】

一、理解自然數(shù)是“1”的積累

出示：數(shù)（shù）源自于數(shù)（shǔ）。

師：這是數(shù)學(xué)家華羅庚爺爺說過的一句話，你讀得懂嗎？

生：數(shù)就是數(shù)出來的。

生：數(shù)就是數(shù)1、2、3、4……這樣數(shù)數(shù)。

師：是的，我們認識的數(shù)就是數(shù)物體時（如，1個物體就是1 個1，2 個物體就是2 個1，3 個物體就是3 個1，接著往下數(shù)……），有幾個1 就是幾。怪不得華羅庚爺爺說數(shù)源自于數(shù)。可是今天我們要認識的數(shù)很奇怪，它不是來自于數(shù)，而是來自于分。你想認識它嗎？

【分析與思考：借助數(shù)學(xué)家的話，通過數(shù)數(shù)進一步使學(xué)生理解自然數(shù)的意義，認識到原來認識的自然數(shù)是在一個物體一個物體疊加的基礎(chǔ)上累計起來的，而新要認識的分數(shù)不是“1”的疊加，而是需要對“1”進行分割，表示分割后的一部分，或者表示部分疊加。這需要打破學(xué)生原有對數(shù)的認識的思維定勢，重新建立新的概念。這里既為下面認識分數(shù)學(xué)習(xí)做好鋪墊，又設(shè)下懸念，激起學(xué)生的探究欲望。】

二、探究二分之一

1.認識二分之一。

課件出示4 個蘋果、2 瓶礦泉水、1 個月餅。

師：姐妹倆去郊游，帶了一些食物，你能幫她們分一分嗎？

生：4 個蘋果，每人2 個。2 瓶礦泉水，每人1 瓶。

師：你真公平，每人分得一樣多，在數(shù)學(xué)上這種分法叫做——平均分。可以列式嗎？

生：4÷2=2（個），2÷2=1（瓶）。

師：那月餅只有1 個，還能平均分給2 個人嗎？

生：可以，一人一半，每人分到半個。

師：怎樣列式？

生：1÷2=

師：算式的結(jié)果怎樣表示呢？

生：每人0.5 個。

生：它表示要先分一分，而且有兩個數(shù)字，中間還有一條線。

師：真會觀察，它表示什么意思呢？我們一起來看。

課件演示：把1 個月餅平均分成2 份的過程。

師：把1 個月餅平均分成2 份，每份是這個月餅的一半，也是這個月餅的

（教師根據(jù)學(xué)生回答依次出示“ ”，“2”，“1”）

教師邊小結(jié)邊介紹分數(shù)的寫法和讀法以及各部分名稱，并板書課題。

【分析與思考：在分1 個月餅的過程中，學(xué)生發(fā)現(xiàn)1 個月餅不夠分給2 個人，需要把它平均分成2 份，其中的1 份（一個月餅的一半）就是這個月餅的。讓學(xué)生感受到分數(shù)產(chǎn)生于對“1”的分割，在分一分、說一說的過程中，將學(xué)生原始認知中形象的“月餅的一半”與抽象的建立聯(lián)系。這是分數(shù)認識的生長點，教師找準概念的生長點，打破學(xué)生原有對數(shù)的認識，擴充新的數(shù)的概念。】

2.創(chuàng)造二分之一。

請拿出學(xué)具袋，同桌選擇一個你喜歡的圖形，用折一折、畫一畫的方法，表示出這個圖形的。

（學(xué)生選擇學(xué)具動手操作）

生：我選擇了圓形，把圓對折，平均分成2 份，其中的1 份就是這個圓的。

生：我選擇了長方形，把長方形對折，平均分成2 份，其中的1 份就是這個長方形的。

學(xué)生介紹后把作品展示在黑板上。

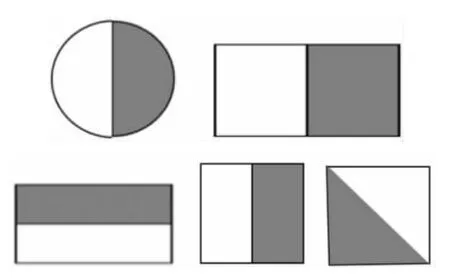
師：觀察2 個正方形（或2 個長方形），折法不同，涂色的形狀也不同，為什么涂色部分都是這個圖形的

生：因為他們都是把正方形平均分成2 份，每一份就是這個正方形的

生：因為他們都是把長方形平均分成2 份，每一份就是這個長方形的

師：看來，折法不是關(guān)鍵，只要把圖形平均分成2 份，每份就是它的

師：（追問）同學(xué)們選擇的圖形不同，涂出每一份的形狀也不同，為什么還是可以用來表示呢？

生：不管是什么圖形，只要是把它平均分成2份，每一份就是它的。

三、認識幾分之一

師： 認識了二分之一，你還想認識幾分之一呢？

師：那下面讓我們來創(chuàng)造一個你想認識的幾分之一吧！

從材料中再拿一個圖形，動手試一試。

（反饋時把學(xué)生的作品展示到黑板上）

師：瞧，這些圖形的形狀不同、涂色形狀也不同，為什么涂色部分都能用來表示？

師：相同的圖形能表示出不同的分數(shù)嗎？

生：只要把一個物體平均分成幾份，每份就是它的幾分之一。

【分析與思考：引導(dǎo)學(xué)生圍繞核心學(xué)習(xí)目標，通過動手操作，自主探究，于互動中生成。通過創(chuàng)造分數(shù)，表述分數(shù)，由二分之一的認識擴展到幾分之一的認識，學(xué)生在動手創(chuàng)作、自我展示中，互相交流、互相啟示，思維不斷被激發(fā)，一步步探尋概念的本質(zhì)，最后水到渠成，自然抽象出幾分之一的數(shù)學(xué)本質(zhì)意義。】

四、練習(xí)拓展

1.看圖寫分數(shù)（略）。

2.分數(shù)墻。

師：我們把剛才這個長方形直條長看作1 米，你能分別寫出下面每份表示的分數(shù)嗎？

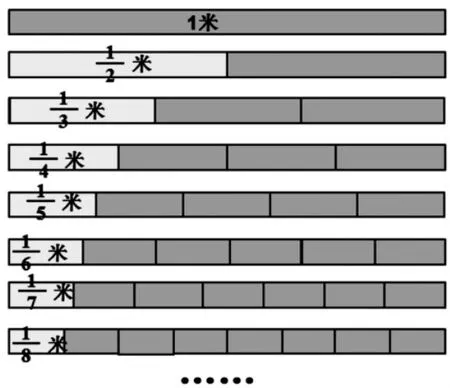
師：仔細觀察這幅圖，你有什么發(fā)現(xiàn)？

生：我們以前認識的數(shù)3 大于2，5 大于4，可是在圖中發(fā)現(xiàn)小于小于，這樣分母大的分數(shù)反而小。

生：我發(fā)現(xiàn)，平均分的份數(shù)越多，所得到的幾分之一越小。

生：我發(fā)現(xiàn)分子都是1，分母越大的分數(shù)反而越小。

3.生活中的分數(shù)。

師：鐘面讓你聯(lián)想到了幾分之一？

【分析與思考：通過“分數(shù)墻”和鐘面的設(shè)計，運用了數(shù)形結(jié)合的方式，不但進一步鞏固了分數(shù)的意義，而且巧妙地滲透了分數(shù)的大小。教師并沒有讓學(xué)生進行分數(shù)的大小比較，學(xué)生在觀察中自然發(fā)現(xiàn)了分數(shù)大小的規(guī)律，進一步完善了對分數(shù)的認識。在鐘面上找分數(shù)中，學(xué)生的思維火花被點燃，為學(xué)生認識幾分之幾的分數(shù)埋下伏筆。】