一種簡易RCS 系統姿態控制方法

張 磊，馬奧家，李亞輝，高 峰，王辰琳

（中國運載火箭技術研究院，北京，100076）

0 引 言

反作用力控制系統（Rejection Control System，RCS）通過對外噴射工質獲得作用于飛行器上的反作用力矩，從而達到控制飛行器姿態的目的。RCS 系統產生的控制力矩相對較小，一般應用于在大氣層外飛行或在稀薄大氣中飛行的飛行器姿態控制中，具有不依賴外部使用環境、控制能力穩定等優點。

隨著飛行器技術的不斷發展，飛行器不斷呈現出小型化的發展趨勢，飛行器內部的裝填空間變得越來越狹小。在滿足飛行器姿態控制需求的前提下，如何降低RCS 系統的規模、降低對飛行器裝填空間的需求成為了需解決的關鍵問題。

傳統的RCS 系統為實現三通道姿態控制，采用8枚以上的姿控噴管[1～3]，系統規模相對較大，對裝填空間有較高要求。本文給出的一種簡易的RCS 系統布局方案，采用4 枚姿控噴管布局，大幅降低了RCS 系統規模，同時，針對該布局存在的三通道耦合影響問題，提出了一種易于工程實現的姿控噴管開關邏輯策略，并設計了控制律，實現了三通道姿態的穩定控制。

1 RCS 姿態控制系統

本文給出的RCS 系統姿控噴管布局方案如圖1 所示。4 枚姿控噴管安裝于飛行器尾部某一平面上，姿控噴管向飛行器外側噴射工質，反作用力方向指向飛行器內側，推力作用線平行于象限間的45°線。

圖1 RCS 系統噴管布局Fig.1 RCS System Nozzle Layout

同時打開任意兩枚姿控噴管即可實現單通道姿態控制，共有6 種不同打開組合，分別與三通道獨立控制時的6 種控制力矩方向需求相對應，可以實現三通道的獨立姿態控制。當僅打開1 枚姿控噴管或同時打開3 枚姿控噴管時將產生三通道控制力矩，共有8 種不同的打開組合，分別與三通道同時控制時的共8 種控制力矩方向需求相對應，可以實現三通道的姿態控制。

噴管開關組合與控制力矩方向對應關系如表1 所示（4 枚噴管同時打開時不產生控制力矩，與噴管全部關閉時力矩相同，表格中不重復列出）。俯仰、偏航和滾動三通道的控制力矩需求組合共有27 種，而本文的姿控噴管布局方案僅能產生15 種不同的力矩組合形式，無法產生的12 種力矩組合為雙通道有控制力矩需求時的組合。因此，在進行雙通道姿態控制時，或是僅進行單通道姿態控制，暫時不對另一通道進行控制，或是產生三通道的控制力矩，實現雙通道控制的同時不可避免的引入了對另一通道的耦合干擾。

表1 噴管開關組合與控制力矩對照表Tab.1 The Comparison Table of Switch Combinations and Control Moment

2 RCS 系統姿態控制方案

2.1 控制率設計

采用極限環進行姿態控制[4,5]，以俯仰通道為例，控制指令計算方法如式（1）所示。俯仰、偏航和滾動通道控制指令分別用Kφ、Kψ和Kγ表示。當控制指令為-1 時，表示該通道有負向控制力矩需求；為1 時表示有正向控制力矩需求；為0 時表示沒有控制力矩需求。控制特性示意如圖2 所示。

式中 m 為回環系數；A 為控制門限；a 為動態增益；?為俯仰角； ?Δ 為俯仰角偏差； ?˙Δ 為俯仰角速度。

圖2 控制特性示意Fig.2 Schematic Diagram of Control Characteristic

2.2 姿控噴管開關邏輯

在上述姿控噴管布局的基礎上，制定姿控噴管開關邏輯時的主要策略如下：

a）單通道控制和三通道控制時，不存在通道間耦合影響，根據控制力矩需求直接分配姿控噴管產生相應的控制力矩；

b）在進行雙通道控制時，引入三通道的控制力矩進行姿態控制。在實現雙通道控制的同時，引入了對另一通道的干擾；

c）雙通道的控制力需求均與兩組三通道控制力矩需求相對應（如Kφ=Kψ=1時，對應Kφ=Kψ=Kγ=1和Kφ=Kψ=1，Kγ=-1 兩種情況），在使用時遵循噴管使用最少原則，選擇僅開啟1枚噴管的開關邏輯來實現雙通道的控制。

根據以上控制策略確定噴管開關邏輯如表2所示。

采用以上開關邏輯進行姿態控制，雖然在進行雙通道控制時引入了對另一通道的干擾，但飛行器姿態在控制力矩和干擾力矩的雙重作用下將逐漸轉化為三通道姿態控制或單通道姿態控制問題，最終實現飛行器姿態的動態穩定。下文的仿真結果也證明了這一點。

表2 姿控噴管開關邏輯表Tab.2 Switch Logic of the Attitude Control Nozzles

2.3 動力學模型

由于RCS 系統主要工作于稀薄大氣或是大氣層外飛行時段，因此忽略了大氣等外部飛行環境影響。并且RCS 系統姿控噴管產生的推力量級較小且為斷續作用，對飛行器質心運動的影響很小，因而在進行仿真分析時忽略了質心運動的影響，僅分析飛行器姿態的穩定性。飛行器動力學模型為[6～8]

式中 ?，ψ ，γ 分別為俯仰角、偏航角和滾轉角；x1ω ，ωy1，ωz1分別為俯仰、偏航和滾轉角速度； Jx， Jy， Jz為轉動慣量；Mcx1，Mcy1，Mcz1為三通道控制力矩；Mdx1，Mdy1，Mdz1分別為三通道干擾力矩。

以僅打開噴管1 為例，產生的三通道控制力矩計算公式如下：

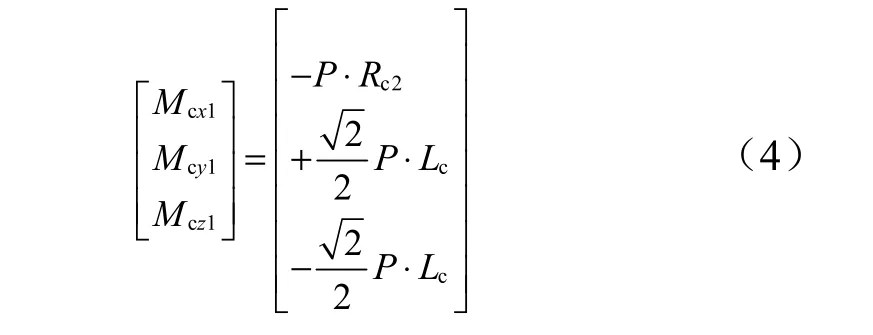
式中 Lc為姿控噴管在俯仰、偏航通道上的作用力臂；Rc2為姿控噴管在滾動通道上的作用力臂；P 為單個噴管的推力。噴管力臂示意見圖1。

定義：P·Rc2=Mr，P· Lc=M，式（4）可以表示為

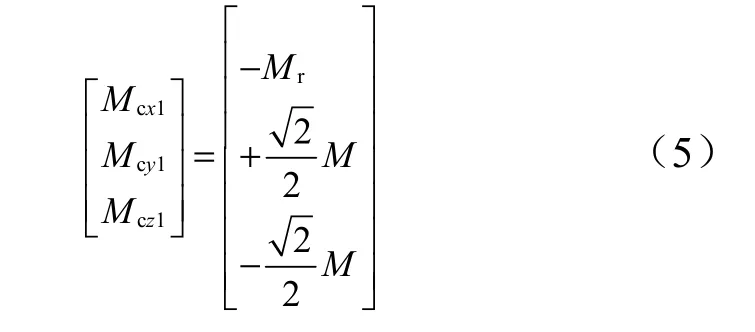
式中 Mr為單位滾動通道控制力矩；M 為單位俯仰、偏航通道控制力矩。

定義：Mcx1/Mr=，Mcy1/M=，Mcz1/M=。則當僅打開噴管1 時，通道等效控制指令為

其他噴管打開時的等效控制指令計算方式與噴管1類似，因此也能夠得到多個噴管同時打開時的等效控制指令，可以據此分析姿控噴管的解耦狀態。

3 仿真分析

3.1 仿真條件

為驗證姿態控制方案的有效性設計了仿真算例。姿態控制系統跟蹤姿態指令，俯仰、偏航通道包括姿態調整及姿態保持等指令，滾動通道為姿態保持指令。

仿真時飛行器初始參數如表3 所示。

由于存在姿控噴管推力偏斜等干擾因素，在仿真中需要引入對應的干擾力矩。為引入簡便且達到貼近真實工況的目的，在進行單通道控制時，在另外兩個通道同時產生通道控制力矩1%的干擾力矩，以進行俯仰通道控制為例，在偏航通道將產生0.3 N·m 的干擾力矩，滾動通道將產生0.03 N·m 的干擾力矩。在進行三通道或雙通道控制時，由于三通道均產生了控制力矩，作為小量的干擾力矩則可以忽略。

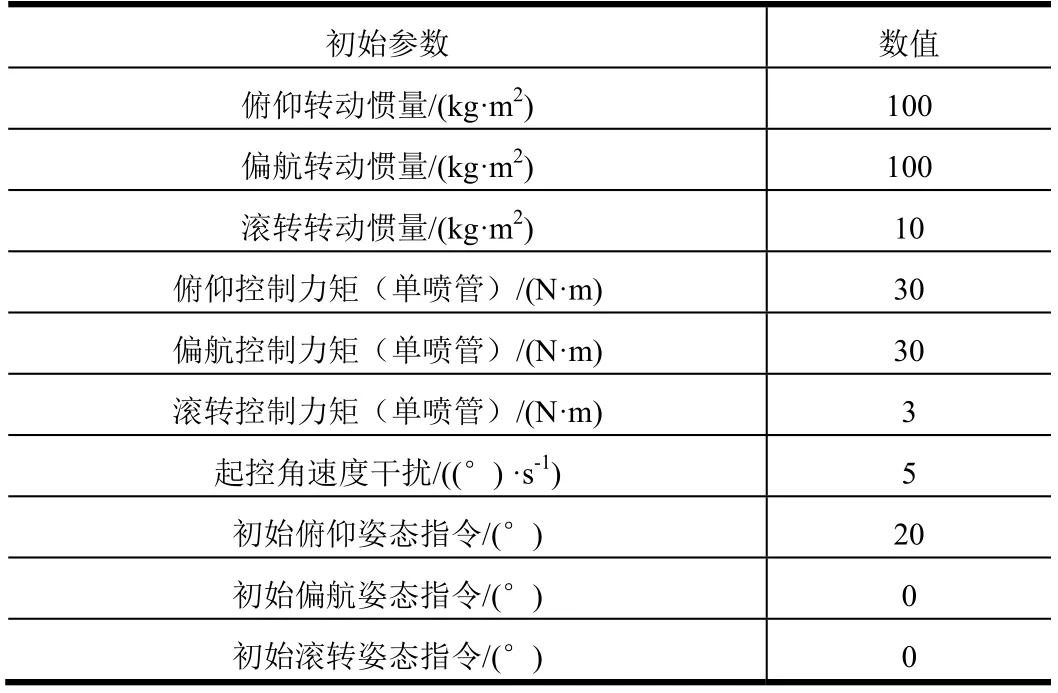
表3 仿真初始條件Tab.3 The Initial Condition of Simulation

3.2 仿真結果

采用上文所述的動力學模型、姿態控制方案和仿真初始條件，完成了控制參數設計和仿真分析。

圖3、圖4 為三通道姿態跟蹤曲線。

圖3 俯仰、偏航姿態角跟蹤曲線Fig.3 Tracking Curve of Pitch and Yaw Attitude Angle

圖4 滾轉角跟蹤曲線Fig.4 Tracking Curve of Roll Angle

由圖3 和圖4 可以看出在姿態穩定段和姿態調整段均能保證姿態穩定，同時在姿態調整時有很好的跟蹤效果。

仿真部分時段的三通道等效姿態控制指令如圖5所示。從圖5 中可以看出，在進行多通道控制時，本文給出的姿控噴管開關邏輯工作正常，在出現通道耦合時，姿控系統有效的對姿態控制指令進行了解耦，實現了三通道穩定控制。

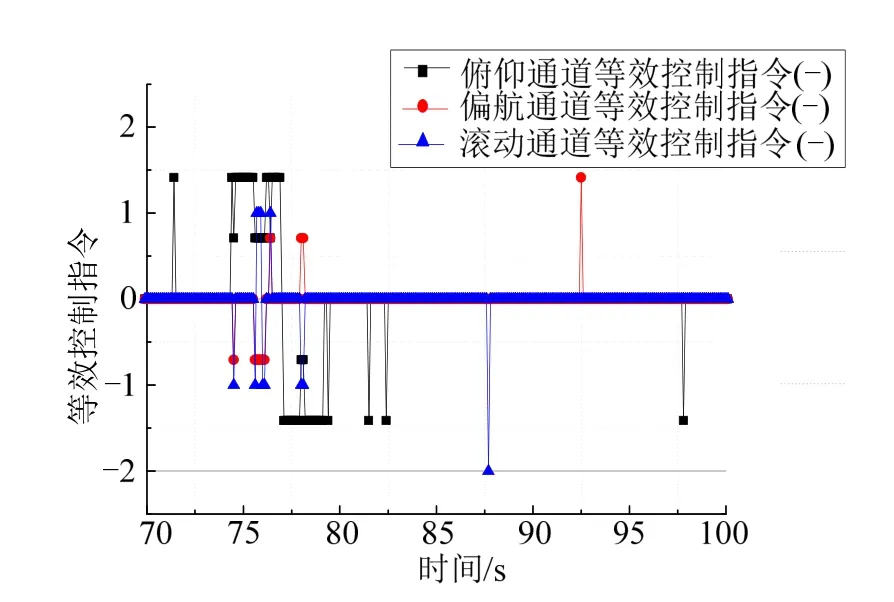
圖5 等效姿態控制指令Fig.5 Equivalent Attitude Control Command

4 結 論

在保證三通道穩定控制的前提下，本文給出了一種新型RCS 系統姿控噴管布局方案，有效地對RCS系統進行了簡化。針對該布局存在的雙通道控制時無法完全解耦問題，給出了一種易于工程應用的姿控噴管開關邏輯策略并設計了控制律，有效實現了三通道姿態穩定控制。通過數學仿真分析證明了姿控噴管布局方案和開關控制邏輯的有效性。