基于Teamcenter VSA 的導引頭安裝精度分析
王聰偉,卞亞東,張 晶,宋 磊,許俊偉
(中國運載火箭技術研究院,北京,100076)
0 引 言
導引頭相對于慣組的安裝精度是末制導設計中的重要精度指標,對于末制導精度具有重要影響,因此往往提出較高精度要求[1~3]。該安裝精度取決于尺寸鏈中相關結構自身幾何偏差和配合面精度。
某飛行器提出導引頭相對于慣組在俯仰方向和偏航方向的精度不超過±20′,其部分結構布局如圖1 所示。

圖1 結構布局Fig.1 Structure Layout
導引頭與儀器艙通過斜螺釘連接,儀器艙與彈體通過徑向螺釘連接,慣組通過慣組梁安裝于彈體側壁。相比于常規導彈布局,該結構布局具有以下特點:
a)中間傳遞環節多,累積偏差大;
b)插接結構較多,引起的彈軸偏斜較大。
由于以上因素影響,經過尺寸鏈計算,導引頭相對于慣組的安裝精度較低,難以滿足設計要求,需對尺寸精度設計進行優化。本文利用Teamcenter VSA 三維尺寸鏈分析,以概率方法計算上述安裝精度,同時進行各組成環影響度分析,進而對精度設計進行優化[4,5]。
1 三維尺寸鏈分析模型建立
與本文尺寸鏈分析相關結構包括導引頭、儀器艙、彈體、慣組梁和慣組。封閉環為導引頭相對于慣組的安裝精度;組成環包括導引頭與儀器艙的配合間隙、儀器艙前后端框同軸度、儀器艙與彈體的配合間隙、彈體軸線相對于其前端框偏斜角度、慣組梁安裝精度和慣組安裝精度。具體設計精度如表1 所示。
在Teamcenter 中建立分析模型,如圖2 所示。根據尺寸鏈計算需要,建立特征、公差及裝配關系,如表2、表3 所示。以導引頭天線前端面為基準,建立了慣組與基準面間的俯仰和偏航角度測量,如圖3 所示。

表1 尺寸設計精度Tab.1 Dimension Precision

表2 尺寸鏈分析模型特征及公差建立Tab.2 Features and Tolerances of Dimension Chain Analysis Model

表3 裝配關系建立Tab.3 Establishing Assembly Relationships
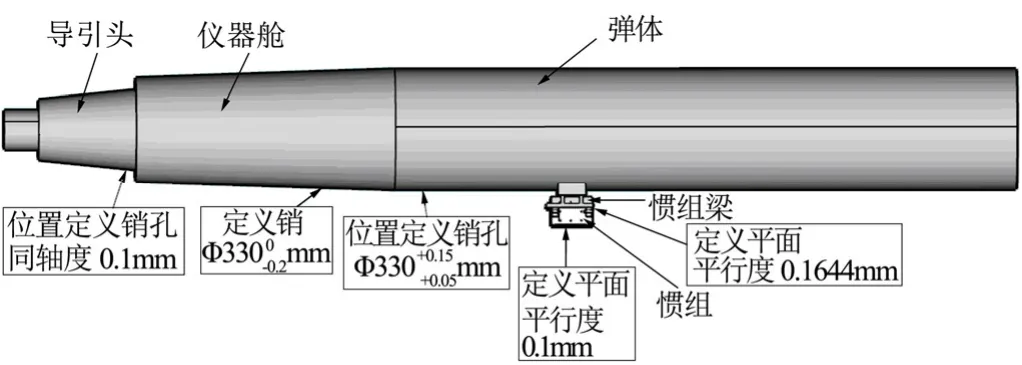
圖2 三維尺寸鏈分析模型Fig.2 3D Dimension Chain Analysis Model

圖3 建立角度測量Fig.3 Establishing Angle Measurement
2 計算結果分析
2.1 仿真模型設置
Teamcenter VSA 通過蒙特卡羅方法仿真模擬了零件加工和裝配過程中的概率分布,即對所有尺寸和裝配關系進行隨機組合,用來預測封閉環的尺寸分布;通過HLM(High-Low-Median)仿真分析各尺寸和裝配關系對目標尺寸的影響程度。具體仿真參數設置如表4 所示。尺寸鏈中各環節均按正態分布進行設置,考慮該產品為首次生產裝配,合格率設置為99.73%(±3σ)[6,7]。

表4 Teamcenter VSA 仿真設置Tab.4 Simulation Setup of Teamcenter VSA
尺寸鏈仿真結果中主要包含以下重點內容[8]:
a)尺寸分布的中間值(μ);
b)設計下偏差(Lower Spec Limit,LSL)和設計上偏差(Upper Spec Limit,USL);
c)產品合格水平(Cp),Cp<1 說明合格率低于99.73%,但追求過高Cp會降低經濟性。
2.2 相對安裝精度分析
2.2.1 俯仰方向精度分析
俯仰方向安裝精度仿真結果如圖4 所示,重點仿真數據如表5 所示。由圖4、表5 可知,該結果呈正態分布,左右極值均為31.6′(±3σ),不能滿足±20′的設計要求,不合格率達到6%。

表5 俯仰方向仿真數據Tab.5 Simulation Data of Pitch

圖4 俯仰方向安裝精度仿真結果Fig.4 Simulation Result of Pitch
俯仰方向安裝精度各環節影響度分析如表6 所示。

表6 俯仰方向安裝精度影響度分析Tab.6 Effects of Installation Precision in the Pitch Direction
由表6 可知,前兩個環節對俯仰方向安裝精度的貢獻共達到94.62%,屬于主要影響因素,應在保證工藝性的基礎上,嚴格控制其公差;后兩個環節總占比僅5.38%,可以適當放松公差要求,降低生產成本和周期。
2.2.2 偏航方向精度分析
偏航方向精度仿真結果如圖5 所示,重點仿真數據如表7 所示。由圖5、表7 可知,該結果呈正態分布,左右極值均為31′(±3σ),不能滿足±20′的設計要求,不合格率為5.52%。

圖5 偏航方向安裝精度仿真結果Fig.5 Simulation Result of Yaw

表7 偏航方向仿真數據Tab.7 Simulation Data of Yaw
偏航方向安裝精度各環節影響度分析如表8 所示。

表8 偏航方向安裝精度影響度分析Tab.8 Effects of Installation Precision in the Yaw Direction
由表8 可見,與俯仰方向安裝精度分析類似,前兩個環節對偏航方向安裝精度的貢獻共達到95.66%,屬于主要影響因素,應在保證工藝性的基礎上,嚴格控制其公差;后兩個環節總占比僅4.33%,可以適當放松公差要求,降低生產成本和周期。
3 設計精度優化
由2.2 節仿真結果和影響因素分析可知,目前的設計精度尚不能滿足安裝精度要求,且尺寸鏈各環節影響程度差異較大。因此,在保證慣組安裝精度的前提下,本節對原尺寸精度進行了優化,見表9。

表9 改進后設計精度Tab.9 Dimension Precision after Improvement
優化后導引頭相對于慣組的安裝精度仿真結果如圖6、圖7、表10~13 所示。

圖6 俯仰方向安裝精度仿真結果Fig.6 Simulation Result of Pitch

圖7 偏航方向安裝精度仿真結果Fig.7 Simulation Result of Yaw

表10 俯仰方向仿真數據Tab.10 Simulation Data of Pitch

表11 俯仰方向安裝精度影響度分析Tab.11 Effects of Installation Precision in the Pitch Direction

表12 偏航方向仿真數據Tab.12 Simulation Data of Yaw

表13 偏航方向安裝精度影響度分析Tab.13 Effects of Installation Precision in the Yaw Direction
分析結果表明:俯仰和偏航方向安裝偏差均有所減小,尺寸鏈各環節影響程度更加均勻,尺寸精度分配更加合理。
4 結束語
本文利用Teamcenter VSA 三維尺寸鏈分析軟件對某飛行器結構之間的相對安裝精度進行了分析,并實現設計精度的優化分配,有效提高了相對安裝精度和工藝性。該三維尺寸鏈分析方法能夠實現概率分布下精度分析、各組成環節敏感度分析和精度優化設計,可在復雜結構和機構尺寸鏈分析中得到廣泛應用。

