底泥磷釋放對藻類種群動力學的影響

郝麗娜， 虎佳堯， 李永坤

(長春工業大學 數學與統計學院， 吉林 長春 130012)

0 引 言

水生生態系統在人類的生活環境中起著十分重要的作用。伴隨著人口不斷增加、城鎮化進程不斷加速,以及工農業不斷發展，整個水生態系統受到非常嚴重的影響，如水生態系統的自凈能力變弱、流動水域更新和交替的周期變長等，都使得水生態系統的富營養化變得更嚴重[1]。丹麥生態學家Jorgensen[2]認為水體中的浮游動物和藻類的生長是水體富營養化的主要原因。因為在短時間內，藻類生物的瘋狂繁殖導致了水華現象此起彼伏。因此對人類的生存、健康和整個社會環境造成了很大影響。

在整個水生態系統中，底泥在其中扮演著“源”和“匯”的角色，它能夠不斷接收水體中的沉積物，同時朝水體釋放營養，在水生態系統中具有舉足輕重的地位，發揮著無可替代的作用[3-8]。淺水湖的底泥營養鹽釋放是個非常復雜且重要的過程。但是大多數研究集中在生物學或者生態學上，以野外實驗或者實驗室數據分析為主，探討因素之間的作用關系[9-14]。

另外，一些相關研究建立帶有底泥系統的營養鹽循環的數學模型，但是往往以數值計算和模擬為主[16-18]，對底泥系統的機理性分析并不多見，且不深入，關于底泥系統的種群動力學模型更是鮮見。

生態種群動力學是一個以數學理論和方法研究生態學的重要分支，具有廣闊的應用范圍和發展空間，生態種群動力學已廣泛應用于水生態系統問題研究中[19-21]。因此,文中應用生態種群動力學模型系統地研究底泥對藻類爆發的影響，從而為底泥疏浚和控制藻類爆發提供一定的理論依據。主要研究內容包括以下幾方面：

1)基于種群動力學建立關于營養元素(磷)-藻類-浮游動物的生態數學模型；

2)利用定性分析理論分析模型的動力學行為；

3)對模型進行數值分析；

4)討論底泥疏浚對藻類爆發的影響機制。

1 模型建立

考慮一個由藻類、浮游動物、可溶性磷、底泥和外部流入磷構成的水生態磷循環系統，可溶性磷被藻類作為營養成分吸收，而藻類的死亡和新陳代謝又會分解磷返回到水體中，同時水生態系統底泥中磷不斷釋放到水中，構成一個循環系統，如圖1所示。

圖中，A(t)、P(t)和Z(t)分別為時間t時藻類的密度、水中可溶性磷的密度和浮游動物密度，單位分別為mgC/L,mgP/L,mgC/L，簡記為A、P、Z。

由圖1可知，被藻類利用吸收的可溶性磷來源有四種方式：外部流入的磷、底泥中磷的釋放、浮游動物和藻類死亡或新陳代謝后被分解產生的磷。輸出則主要歸因于藻類吸收的磷和水體的稀釋作用。藻類依靠吸收營養物質(磷、氮等)生長，通過被其它動物捕食、自然死亡和內部競爭從水中消除。

根據藻類的營養吸收速率與溫度g(T)和光照h(Iin,A)有關[19]，為了簡化，文中假設水生態系統的環境溫度和日常光照強度都是保持恒定不變的，即

g(t)=h=1，

可以建立數學模型

(1)

式中：D=f(P)A;

bA2----藻類種群內部競爭損失;

aPs----釋放到水中的可溶性磷，其中包含外部流入和底泥中釋放的磷;

a----水體對可溶性磷的稀釋比例;

qa----藻類的磷碳比，即藻類體內磷與體內碳比例，其影響藻類對磷的吸收;

aP----水體對可溶性磷的稀釋造成的損失。因此，aPs-aP代表水體內部與外部的營養交換;

θ1m1A----藻類經過新陳代謝和死亡后按照比例θ1分解釋放的可溶性磷;

θ2m2Z----浮游動物經過新陳代謝和死亡后按照比例θ2分解釋放的可溶性磷。

假定藻類的損失率與密度A成正比，系數為m1；藻類的增長受可溶性磷影響，其增長率為

式中：m----半飽和參數。

浮游動物通過捕食藻類生長，假設捕食功能性反應函數為HollingI型，即

g(A)=cA，

式中：c----捕食率。

水體中可溶性磷的流入部分可表示為

Ps=Pin1+γ1(βPin2+Pb)+γ2(1-β)Pin2，

(2)

式中：Pin1----可溶性磷濃度;

Pin2----顆粒態磷濃度;

Pb----底泥中磷的濃度。

水體中的可溶性磷濃度跟Pin1、Pin2和Pb都有密不可分的關系。假設外部的磷以恒定速率Pin=Pin1+Pin2流入，底泥中的磷Pb和顆粒態磷Pin2分別以γ1和γ2的速度釋放可溶性磷到水中，顆粒態磷Pin2按比例β沉淀到底泥中。

由于底泥中磷的釋放作用，式(2)可簡化為

Ps=P0+γ1Pb。

(3)

文中忽略藻類和浮游動物由于死亡而釋放到底泥中顆粒磷。

2 定性分析

對模型(1)進行分析，設:

G1A-m1A-bA2-cAZ，

aP0+aγ1Pb-G2A-aP+G3，

G3=θ1m1A+θ2m2Z。

經計算可得模型(1)的Jacobian矩陣為

式中：F1=G1-m1-2bA-cZ;

F3=θ1m1-G2;

系統(1)可能存在三類平衡點，邊界平衡點

E1=(0,0,P1),

E2=(A2,0,P2),

E3=(A3,Z3,P3)。

為求得平衡點，需解下面方程組

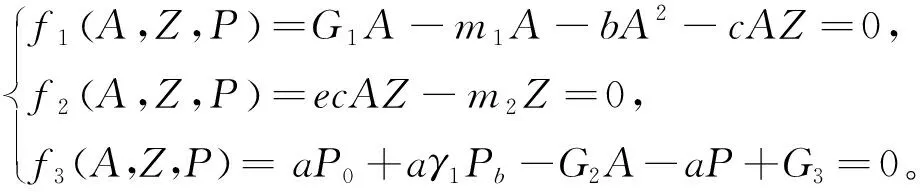
(4)

首先求

E1=(0,0,P1)，

由

aP0+aγ1Pb-aP1=0 ，

解得

P1=P0+γ1Pb。

因此求出邊界平衡點

E1=(0,0,P0+γ1Pb)。

系統(1)在點E1的Jacobian矩陣為

下面求J(E1)的特征值,即

|λE-J(E1)|=0，

可得

解得

λ2=-m2<0,

λ3=-a<0。

因此當

時，

E1=(0,0,P0+γ1Pb),

是局部漸近穩定的。

綜上分析可得定理1。

定理1系統(1)的邊界平衡點E1=(0,0,P1)總是存在，且當

成立時，它是局部漸近穩定的。

下面分析平衡點E2=(A2,0,P2)的存在性和穩定性。因為A=A2,Z=0,P=P2滿足方程組(4)，所以滿足

(5)

aP0+aγ1Pb-G4A2-aP2+θ1m1A2=0,

(6)

由式(5)解得

由式(6)解得

φ(P2)和ψ(P2)的函數圖像如圖2所示。

由圖2可知，在φ(P2)中A2關于P2是單調遞增的，而在ψ(P2)中A2關于P2是單調遞減的。當P2=Ps=P0+γ1Pb時，ψ(P2)=0。

因此由介值定理可得，若φ(Ps)>0，則存在唯一一點P2，使得φ(P2)=ψ(P2)，對應函數值記為A2，于是可得系統(1)的邊界平衡點為E2(A2,0,P2)。

系統(1)在E2的Jacobian矩陣為

其特征方程為

|λI-J(E2)|=(ecA-m2-λ)(K1-K2),

式中：K1=(-bA2-λ)(-H3-a-λ);

K2=H2(θ1m1-G4)。

綜上分析可得定理2。

定理2當φ(Ps)>0時，系統(1)存在邊界平衡點E2(A2,0,P2)，且當

ecA-m2<0,

和

bA2(H3+a)-H2(θ1m1-G4)>0,

成立時，則平衡點E2(A2,0,P2)是局部漸近穩定的。

對于系統(1)的正平衡點E3=(A3,Z3,P3)，A=A3,Z=Z3,P=P3是方程組 (4)的解，因此有

O1=θ1m1A3;

O2=θ2m2Z3。

化簡得

(7)

(8)

aP0+aγ1Pb-G5A3-aP3+O1+O2=0,

(9)

由式(7)得

式中：Q=m1+bA3+cZ3。

把上式代入式(9)可整理得

再由式(7)整理可得

μP3=mQ+P3Q,

即

(μ-Q)P3=mQ,

解得

定義兩個函數

顯然R(Z3)關于Z3遞減，T(Z3)關于Z3遞增，若兩曲線在第一象限有交點，且坐標點為(Z3,P3)，則得E3=(A3,Z3,P3)。進一步利用Jacobian矩陣

判斷E3是否為局部漸近穩定的。由于系統(1)的復雜性，文中沒有給出關于局部穩定性的判據。

3 數值分析

對系統(1)進行了定性分析，研究系統平衡點類型及其存在條件，使用Jacobian矩陣討論了邊界平衡點的局部漸近穩定性。然而，由于該系統具有非線性和復雜性，因此未實現系統全局穩定性的結果。為更加直觀地說明系統的動力學行為，利用數值模擬分析水生態系統中的藻類動力學行為。

系統參數取值見表1。

首先研究系統(1)中底泥中磷的不同濃度(Pb)對系統動力學行為的影響，如圖3所示。

由圖3可以看出，當Pb較低時(Pb=0.5)，系統只存在少量可溶性磷，藻類和浮游動物滅絕(見圖3(a))；

當Pb增加時(Pb=0.65)，藻類可以生存，浮游動物滅絕(見圖3(b))；

當Pb較大時(Pb=0.9或Pb=1.2)，藻類和浮游動物穩定共存(見圖3(c)和(d))；

當Pb繼續增加(Pb=1.4)，藻類和浮游動物穩定共存，達到穩定狀態時的種群密度也會隨著Pb的增加而增加(見圖3(e))。

水生態系統中種群存在的種類和數量會隨著底泥磷釋放的濃度變化而變化。當底泥磷釋放濃度較低時，由于水體中可溶性磷濃度太低，不足以支撐藻類生長所需養分，因此藻類不會在磷濃度過低的水體中生長，所以它的浮游動物也不會出現。隨著底泥磷釋放濃度逐漸增高，藻類開始慢慢繁殖，但此時浮游動物由于藻類的質量不好和數量不足難以生存，同時由于藻類的死亡和其種群內部競爭作用造成的藻類數量以一定的比例損失，藻類就會和底泥磷釋放濃度在密度上達到一定平衡。當底泥磷釋放濃度繼續升高時，藻類就會大量繁殖，當藻類的質量和數量能夠滿足它的浮游動物生存時，底泥磷的濃度、藻類和浮游動物的密度就會達到一定的平衡。

水體稀釋速率變化對系統(1)的影響如圖4所示。

我們考慮當底泥磷釋放濃度(Pb)恒定，水體對可溶性磷的稀釋速率a對系統動力學行為的影響(見圖4)。當a較大時，系統中可溶性磷可以維持藻類和它的浮游動物共存(見圖4(a))；當a減小時，系統中可溶性磷只能維持小部分藻類穩定生存，它的浮游動物逐漸走向滅絕(見圖4(b)和圖4(c))；當a很小時，由于水體對可溶性磷的稀釋作用過強，系統中可溶性磷含量過少，藻類和浮游動物均滅絕(見圖4(d))。由此可見，水體對可溶性磷的稀釋速率越大，藻類賴以生存的養分不充足，藻類數量就會越少。

表1 模型1中參數的定義、單位和取值

4 結 語

應用種群動力學來研究水生態系統中底泥磷釋放對藻類種群動力學的影響。首先根據種群動力學建立了關于營養元素-藻類-浮游動物數學模型。利用定性分析理論討論了該系統中可能存在的平衡點類型,以及邊界平衡點的局部漸近穩定性。

利用數值分析討論了系統中底泥磷釋放和水體稀釋比例對藻類種群動力學行為的影響。隨著底泥磷釋放濃度的不斷升高，系統經過了以下演變：藻類-浮游動物種群均滅絕、只有藻類種群存在、藻類種群和浮游動物種群穩定共存。只有總磷濃度適中的時候,兩種群達到穩定共存。

在防治和治理水體中藻類爆發災害時,可以考慮對水體底泥進行疏浚，通過降低底泥磷釋放濃度,或者增加水體中稀釋速率來抑制藻類生長。

文中只考慮底泥磷釋放濃度對系統的影響。實際上底泥磷的釋放是個復雜的過程，影響因素很多，既有生物因素，也有非生物因素，可以將每個因素在模型中刻畫描述，并加以研究。另外，文中假設底泥中磷含量為常值，實際上底泥中磷含量是時變的，因此也可以考慮底泥中磷含量是狀態變量的系統來研究。

隨著科學技術的進步，隨之而來產生越來越多實際且復雜的問題。種群動力學結合各學科領域，為解決問題提供新方法和新視角，將問題簡化，進行定性研究。生物數學一定會有更大的進步和廣闊的發展。