基于溫度場分析的安注管線止逆閥內漏監測方法研究

董曉梅，董俊華，余雛麟，高炳軍

(河北工業大學 化工學院，天津 300130)

全球許多核電廠報告的事件表明，管道中的熱分層會導致管道材料產生過度的熱應力和疲勞，可能導致嚴重的熱疲勞開裂和管道系統的泄漏事故[1]。盡管如此，老式核電站的設計并沒有考慮這種熱效應[2]。導致意外熱疲勞的熱分層現象是由冷熱流體之間的密度差異產生的[3，4]。一種典型的熱分層常發生在連接到反應堆冷卻系統(RCS)的安全注入系統(RIS)中，是由于RCS向安注管線的湍流滲入以及支管止逆閥內漏造成的[5，6]。安全注入系統僅在核電廠發生事故時向核反應堆供應應急水冷卻時才運行，在正常工作狀態下，由于RIS中的所有閥門都關閉，RIS的冷卻劑是隔離的。但是，如果連接硼水箱和一回路主管道支管的閥門可能會出現微量的滲漏，冷水將進人高溫水側的管道[7]，并在一定范圍內形成熱分層。泄漏流量的準確確定對于安注管線的熱疲勞分析至關重要，而由于核管道安注管線流體流動的特殊性，對于存在冷熱流體熱分層、湍流滲入、冷熱交替等復雜流體流動與傳熱現象的問題，目前尚缺乏有效的泄漏監測手段。本研究中，通過流固耦合計算分析評估在RIS管線內漏條件下的熱分層特征，提取止逆閥閥前管道外壁溫度并定義熱分層特征溫度參數，得出該特征溫度參數與泄漏量的定量關系式。 在此，僅以熱安注管線為例進行分析討論。

1 數值計算模型

1.1 物理模型

一回路熱段管內徑為736.6 mm，壁厚為67 mm，長度為4 904 mm，水平放置。安注管內徑為131.78 mm，壁厚為18.26 mm，通過管嘴與水平面呈30°和主管道熱段連接，其上安裝有止逆閥。利用SolidWorks建立含有主管道熱段和安注管的幾何模型，支管末端閥門泄漏的區域是研究的重點，在閥門中建立月牙形的開孔模擬閥門泄漏，如圖1所示，其中閥門開度與泄漏流速的關系由公式(1)表示[8]。

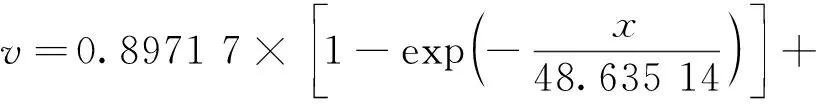
(1)

圖1 幾何模型Fig.1 Geometric model

式中：v——泄漏流體速度，m/s；

x——閥門開度。

1.2 網格劃分與質量檢查

用ANSYS ICEM劃分流體域和固體域的網格，流體域和固體域網格導入Fluent進行流場、溫度場計算。止逆閥和止逆閥內的流體域使用四面體劃分非結構網格，其他流體域和固體域均采用六面體網格，劃分結構化網格。為了盡可能真實地模擬流體混合過程，本文對網格模型進行了網格無關性驗證，計算時，先對模型進行初步網格劃分，在此基礎上，對網格進行加密，直到網格的大小對計算結果影響忽略不計時，才最終的確立網格大小和分布。網格Quality質量低于0.2的網格處在結構和非結構網格的交界面處，對流場和溫度場影響較小。最終網格如圖2所示，網格的數量為75萬個，已具有良好的網格無關性。

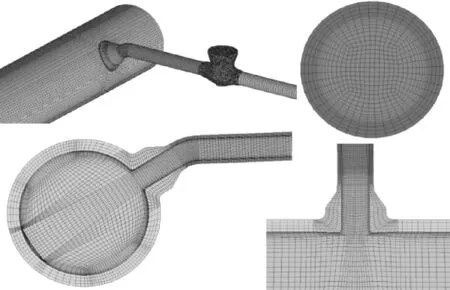
圖2 網格模型Fig.2 Meshof the model

1.3 計算方法

采用三維全尺寸穩態流固耦合傳熱的計算流體動力學(CFD)方法對安注管線發生熱分層現象時的流動與傳熱進行數值研究。與以往的k-ε湍流模型相比，將計算控制區域擴展到安注管管壁所在的固體區域，采用更適合于求解具有流動分離情況的剪切應力傳輸模型Transition SST湍流模型[9]。選擇三維、雙精度、基于壓力隱式求解器，求解控制方程包括連續性方程，質量、能量守恒方程及湍流輸運方程。并將密度處理為溫度的線性函數來估算浮力項的影響。

1.3.1 控制方程

(1)全浮力模型

管內流體溫差較大，且工作在高溫、高壓下，密度隨溫度的變化明顯。因此，本文采用全浮力模型進行計算。在包括浮力的計算中，動量方程需增加1個源項[10]。全浮力模型則根據求解的實際密度通過公式(2)直接對浮力進行評估，進而求解全場浮力。

SM,buoy=(ρ-ρref)g

(2)

式中：SM,buoy——浮力源項，N；

ρ——密度，kg/m3；

ρref——參考密度，kg/m3；

g——重力加速度，m/s2。

(2)連續性方程

(3)

式中：t——時間，s；

xj(j=1，2，3)——直角坐標分量，m；

uj(j=1，2，3)——速度分量，m/s。

(3)動量守恒方程

(4)

(5)

式中：μ——黏性系數，kg/(m·s)；

p——壓力，Pa；

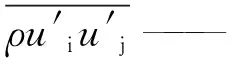
(4)能量守恒方程

(6)

式中：cp——比定壓熱容，J/(kg·K)；

λ——導熱系數，W/(m·K)；

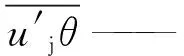
S——能量方程的源項。

(5)k和ω輸運方程

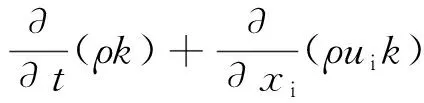
(7)

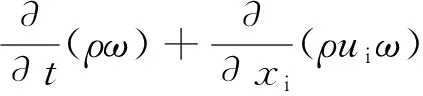
(8)

式中：Gk，Gω——名義速度梯度下k的產生項，ω產生項；

Γk，Γω——k和ω的有效擴散率；

Yk，Yω——k和ω的有效耗散率；

Sk，Sω——用戶自定義源項。

Transition SST數學方程模型在k-ωSST 的基礎上額外增加了兩個輸運方程，分別是間歇度γ和瞬態起始標準，可表示為：

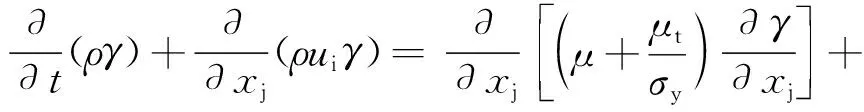
(9)

(10)

有效擴散率Γk和Γω可表示為

(11)

式中：σk和σω——k和ω的湍流普朗特數；

μt——湍流黏度。

(12)

式中：ɑ*可在低雷諾數時限制湍流粘度的大小，ɑ*的定義如下：

(13)

(14)

1.3.2 邊界條件

由于主管和熱安注管外側都有保溫層，所以主管道和熱安注管的外壁設為絕熱邊界。忽略管道端部橫截面傳熱量，因此也設為絕熱邊界。流體域和固體域的交界面設為耦合壁面邊界條件。

熱安注管進口設為速度進口邊界；主管道的流量按功率運行時的流量確定，主管道進口也設為速度入口邊界條件；壓力出口，壓強為15.5 MPa。為了避免進口段對混合過程模擬的影響，消除邊界條件對流場的干擾，同時減小計算量，通過fluent的二次開發UDF，采用DEFINE_ PROFILE編寫，將發展完全后的速度分布添加到主、支管的進口邊界條件中。

1.3.3 物性參數

本文通過自定義材料方式實現材料參數的定義，熱安注管和主管材料為Z2 CN 18-10，假定流體為不可壓縮流體，物性參數采用變物性。金屬材料屬性取自RCC-M規范[11]，對于流體的物理性質，使用基于技術數據中的物性數據將相關性作為溫度的函數進行計算，材料屬性隨溫度變化規律如表1所示。

表1 材料參數表Table 1 Material parameters

1.3.4 模型驗證

為了驗證計算模型的準確性，利用本文的數值計算方法來模擬Nobuo Nakamori試驗工況[12]。得到水平支管某剖面上豎直方向高度H與溫度分布的無量綱關系的模擬數據與試驗數據對比結果如圖 3 所示，模擬溫度與試驗數據較好吻合，相對誤差小于 2%，表明本文所采用的數值計算方法的準確性。圖3中D為支管直徑；T為剖面上某點的溫度；Tmin為剖面上的最低溫度；Tmax為剖面上的最高溫度。

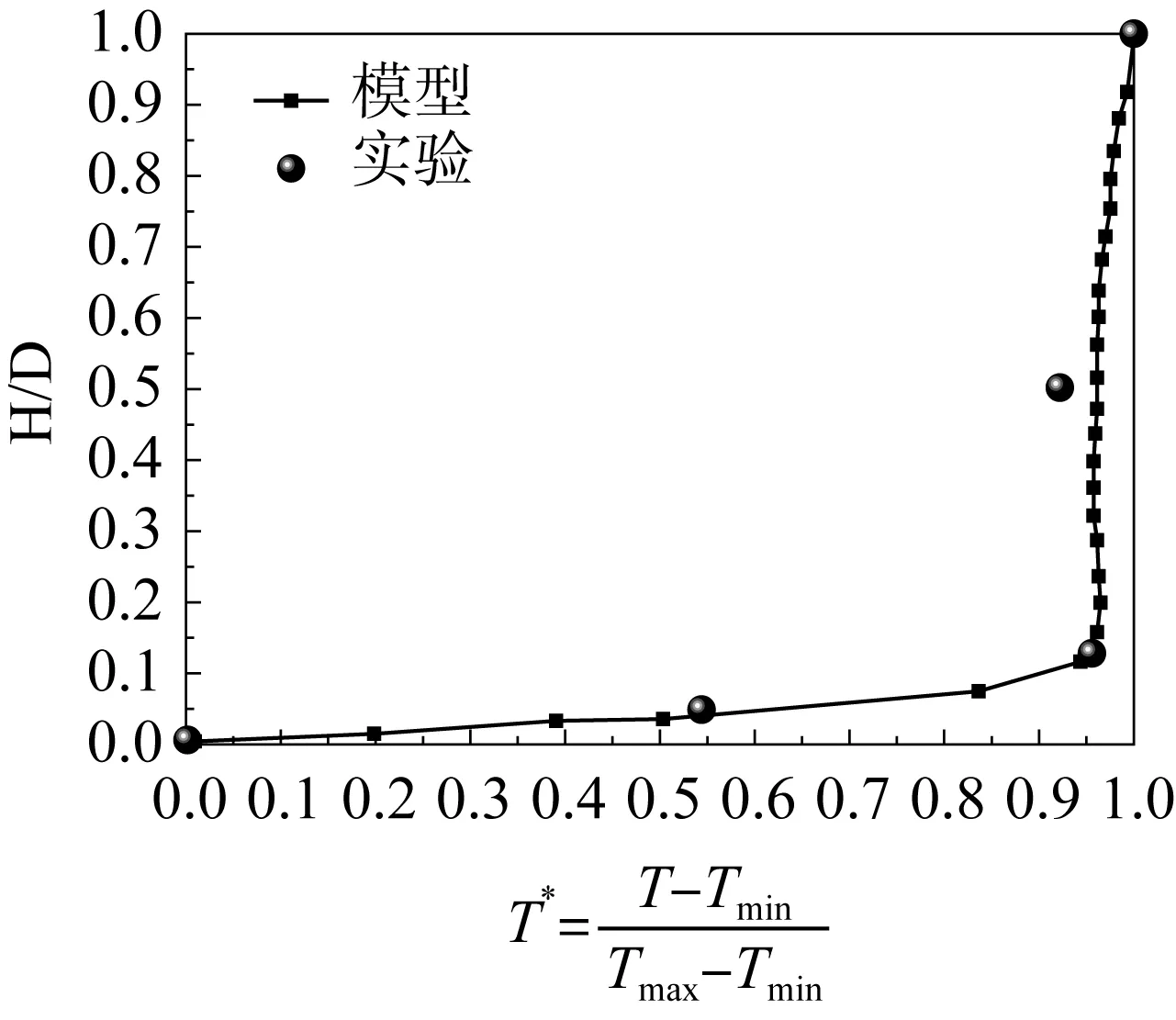
圖3 某剖面高度與溫度分布的無量綱關系Fig.3 No-dimensional relation of temperature and Height in section plane

2 計算方案與結果分析

2.1 計算方案

核電廠主管道內熱水參數受用電負荷影響，是不穩定的。根據閥前主管道流體溫度Thot、流量Qhot及閥后管內泄漏工質的溫度Tcold范圍，主管道內熱流體溫度Thot取564～601 K；流量Qhot范圍為90%～ 110 %Q額(Q額=2.379×107L/h)；安注管泄漏的冷流體溫度Tcold范圍為293～328 K；泄漏量QLeak取5～400 L/h。得出不同工況下的溫度場并獲取閥前監測位置管外壁溫度數據，每一個工況對應一個監測位置的管壁溫度分布。采用單一因子變量法著重分析和探討了一回路主管道與安注管工質參數是如何影響止逆閥前管外壁溫度的。依據數學建模方法，采用非線性回歸模型建立管外壁溫度與影響因素之間的函數關系式。

2.2 計算結果與分析

Thot=599.15 K、Qhot=2.379×107L/h、Tcold=327.15 K、QLeak=400 L/h工況下管外壁溫度分布云圖如圖4 (a)所示，可見近主管道區域受湍流滲入的影響管外壁溫度均勻，而靠近閥門較大的區域內由于流體熱分層管壁溫度上下存在溫差。不同圓周位置上管外壁溫度沿管長的變化如圖4(b)所示，可見管外壁溫度自主管道開始沿管長都呈下降趨勢，但湍流滲入區圓周方向無明顯溫差，熱分層區有溫差，較大范圍內溫差分布規律相似。

圖4 管外壁溫度分布Fig.4 Temperature distribution of the pipe outer surface

不同泄漏流量下閥前50 mm位置橫截面流體與管壁的溫度云圖如圖5所示。由圖可見在所討論的泄漏流量范圍內流體均存在較為明顯的熱分層現象。上部溫度較高，下部溫度較低，最高溫度在最上部，最低溫度在最下部。管壁受分層流體的作用，也呈現相應的溫度變化，即上部溫度高下部溫度低，最高溫度在最上部，最低溫度在最下部。

圖5 不同泄漏流量下截面溫度分布Fig.5 Temperature distribution of cross section under different leakage flow rates

圖6為截面直徑線位置溫度分布曲線，最高最低位置金屬管壁內外溫差很小。直徑線位置流體溫度從高到低是逐漸變低的，熱分層是漸變的，這是由于流體沿垂直方向的擴散與熱傳導造成的。管壁與流體最高最低點溫差均隨泄漏流量增加而增大，泄漏流量為400 L/h時，最大溫差達到105 ℃。

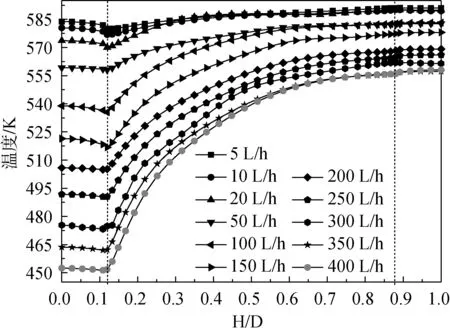
圖6 截面直徑線上溫度分布Fig.6 Vertical temperature distribution of Cross Section

不同泄漏流量時，閥前50 mm管外壁面沿圓周方向溫度分布如圖7所示，溫度分布左右基本對稱，QLeak越大，管外壁溫度越低。

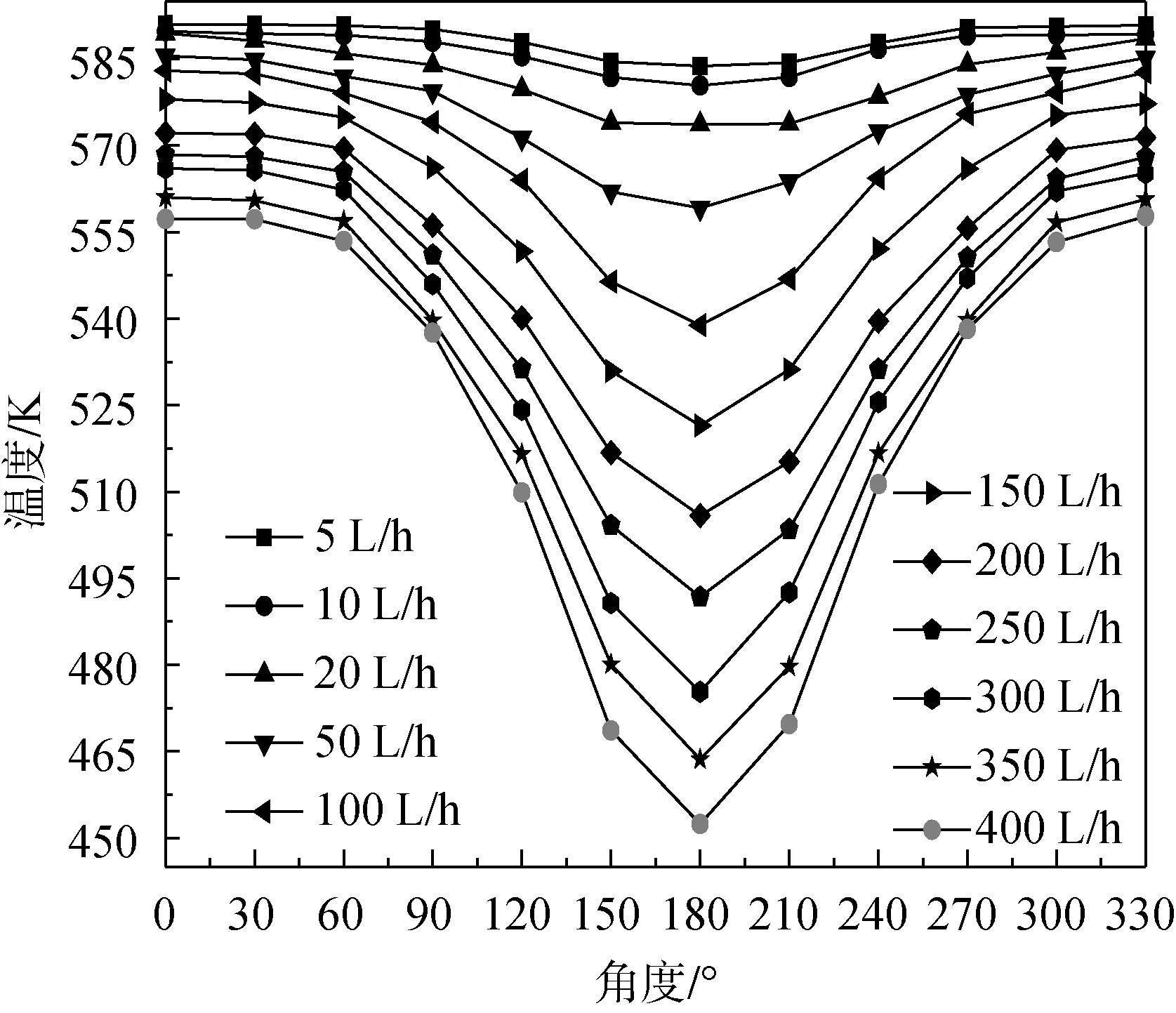
圖7 不同泄漏量下管外壁溫度分布Fig.7 Pipe wall temperatures at various leakage rate

3 泄漏預測模型的建立

3.1 熱分層特征溫度參數

將溫度監測點設在止逆閥前50 mm處的位置AT6B—7，在測量位置的一側沿圓周方向30°等間距安裝7個熱電偶，如圖8所示。根據7個測點溫度可整理如下熱分層溫度特征參數。

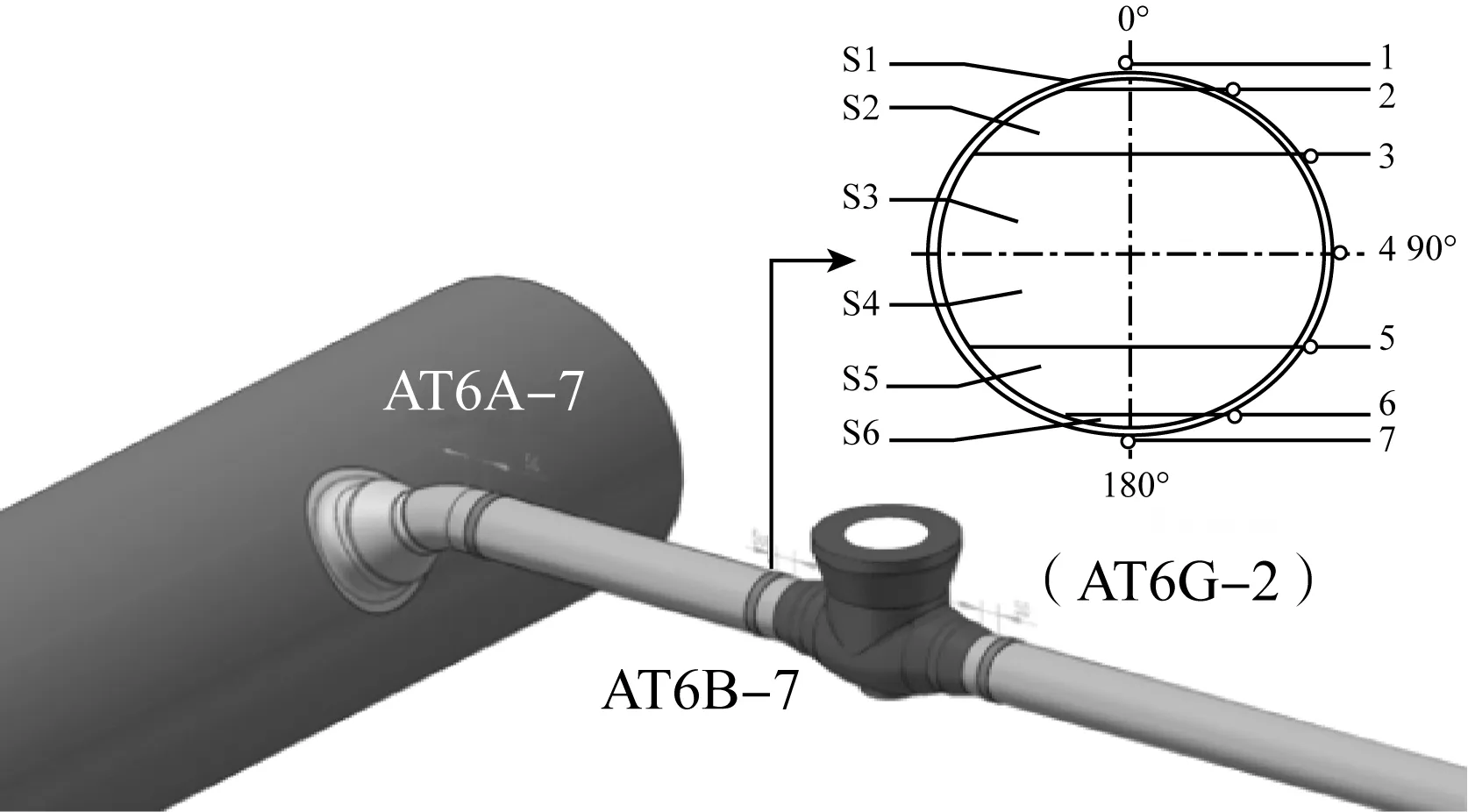
圖8 溫度測點的布置Fig.8 Arrangement of temperature measuring points

令

(15)

(16)

(17)

(18)

(19)

(20)

則熱分層致溫差為

ΔT=T0°-T180°

(21)

熱分層致當量面平均溫度為

(22)

(23)

式中：Si——兩相鄰測溫點間監測截面的面積。

3.2 熱分層特征溫度參數單變量分析

熱分層特征溫度參數隨主管道流體溫度的變化關系如圖9所示，當量面平均溫度TA隨著主管道流體溫度的增加而增加，且呈線性增加趨勢。這是因為主管道內流體的溫度越高，則管壁溫度會直接增大，熱流體的傳熱速率加快，熱流密度的增加從而管壁的溫度相應的增加。主管道溫度增大時，管外壁的溫差ΔT逐漸增大，呈非線性，運用最小二乘法進行擬合時，管壁溫差ΔT與主管道溫度成三次關系。

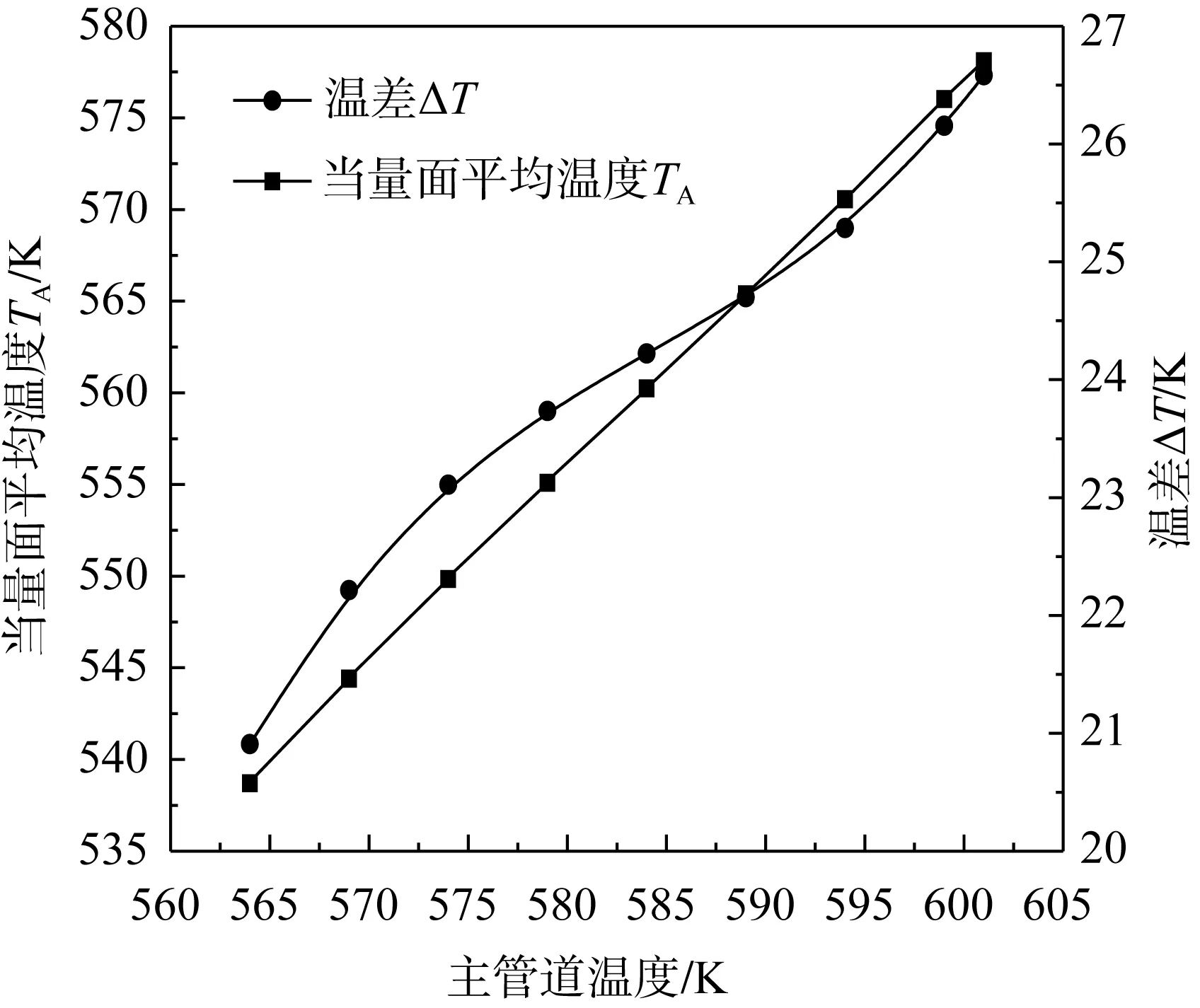
圖9 溫度特征值隨主管道溫度變化關系Fig.9 Variation relationship of characteristic temperature with the main pipe temperature

熱分層特征溫度參數隨主管道流量的變化關系如圖10所示，當主管道內流量逐漸增大時，當量面平均溫度TA呈非線性降低，運用最小二乘法進行擬合時，當量平均溫度TA與主管道流量成冪函數關系。主管道流量增大時，溫差ΔT非線性降低，運用最小二乘法進行擬合時，溫差ΔT與主管道流量成一階指數衰減函數關系。

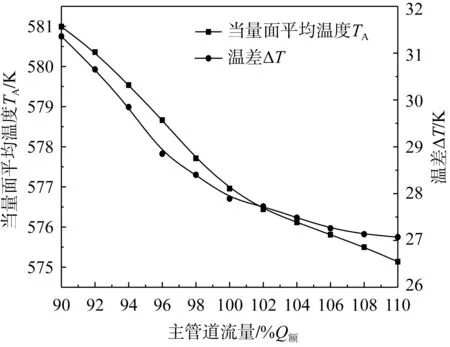
圖10 溫度特征值隨主管道流量變化關系Fig.10 Variation relationship of characteristic temperature with the main pipe flow rate

熱分層特征溫度參數隨泄漏流體溫度的變化關系如圖11所示，當泄漏工質溫度逐漸增大時，當量面平均溫度TA線性增加。管道泄漏工質溫度增大時，管壁溫差ΔT線性降低。

圖11 溫度特征值隨泄漏工質溫度變化關系Fig.11 Variation relationship of characteristic temperature with the leakage flow temperature

熱分層特征溫度參數隨泄漏流量的變化關系如圖12所示，當泄漏工質流量逐漸增大時，監測位置的當量面平均溫度TA有明顯的減小趨勢，且成二次函數關系。當管道泄漏流體的流量增大時，管壁溫差ΔT非線性增大。運用最小二乘法進行擬合時，溫差ΔT與泄漏流量成二次關系。

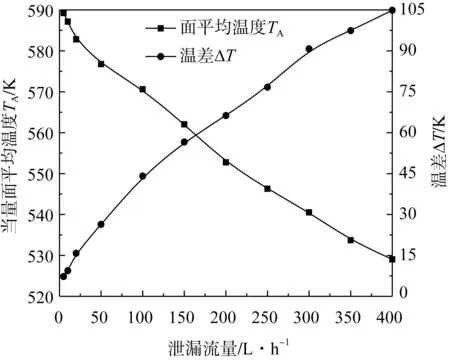
圖12 溫度特征值隨泄漏量變化關系Fig.12 Variation relationship of characteristic temperature with the leakage flow rate

3.3 熱分層特征溫度參數多變量擬合

根據不同工況條件進行的流固耦合計算結果，利用MATLAB統計工具箱中的regress命令，對熱分層特征溫度參數關于主管道內流體溫度Thot、主管道內流體流速Qhot、安注流體溫度Tcold、泄漏流量QLeak進行多變量回歸計算可得

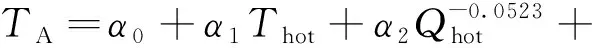
(24)

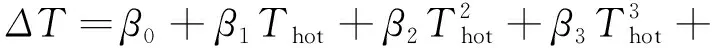
(25)

式中：α0……α5，β0……β7——系數。

TA和ΔT統計計算的R2分別為0.9967和0.9957，表明所定義的熱分層特征溫度參數與回歸變量之間有良好的相關性。

從而可建立內漏流量QLeak的閥門內漏量化預測模型

QLeak,TA=g(Thot,Qhot,Tcold,TA)

(26)

QLeak,ΔT=f(Thot,Qhot,Tcold,ΔT)

(27)

現場泄漏流量計算時，通過現場在閥前管外壁布置的熱電偶，得到測溫點處的溫度，根據公式(15)～公式(23)計算出所述測溫點的當量面平均溫度TA測，將TA測代入到公式(26)中，得到QLeak,TA，根據公式(21)計算出所述測溫點的溫度差ΔT測，將ΔT測代入到公式(27)中，得到QLeak,ΔT，若滿足公式(28)，那么取它們兩個的算數平均值如公式(29)所示，若不滿足，則取兩個之間的較大值如公式(30)所示。

(28)

(29)

QLeak=max{QLeak,TA,QLeak,ΔT}

(30)

3.4 誤差分析

擬合關聯式結果與數值計算結果吻合較好，最大誤差為6.471 7%，可滿足工程閥門內泄漏流量需要。

4 結論

以熱安注管線止逆閥泄漏為例，探討了基于閥前管壁溫度場測量的閥內泄漏流量監測方法。通過流固耦合計算對熱安注管線由于閥門內泄漏造成的熱分層現象進行了詳細分析，定義了閥前監測截面管外熱分層特征溫度參數，通過多變量回歸計算獲取了熱分層特征溫度參數與主管道內流體溫度Thot、主管道內流體流速Qhot、泄漏流體溫度Tcold和泄漏流量QLeak之間的關系式。只要根據閥前監測截面管外壁7點監測溫度獲取熱分層特征溫度參數，即可根據電廠已知參數(主管道內流體溫度Thot、主管道內流體流速Qhot、泄漏流體溫度Tcold)較為準確地預測止逆閥的泄漏流量。