“作、識、用”三管齊下函數圖像巧掌握
◇ 許 陳
函數圖象是函數的一種表達形式,它形象地顯示了相應函數的本質屬性,在實質上與函數解析式是相同的.函數可以把圖象精確化、細微化,反之圖象能使函數直觀化、形象化.高中對函數圖象的要求有三個方面:作圖、識圖、用圖.作圖是基本能力,識圖是綜合素質,用圖是最終目標.
1 作圖
高中階段主要利用描點法作圖.函數的圖象通常是一些連續的曲線或直線,但有時它也可能是幾段光滑曲線,也可能由一些孤立點或幾段線段組成,還可能由折線或射線來構成.
例1函數f(x)=x2+1,試作出對應的圖象,并比較f(-2),f(1),f(3)的大小.

圖1
通過描點法作出函數f(x)=x2+1的圖象,如圖1.其步驟是列表、描點、連線.注意其中的特殊點(0,1),這時函數取最小值.
結合圖象的特征,在第一象限內,y隨著x的增大而增大,則有f(1)<f(2)<f(3),容易發現f(-2)=f(2),即f(1)<f(-2)<f(3).
掌握函數圖象描點法的三步驟,結合函數圖象中特殊點的大小關系或圖象本身的特點,從“數”與“形”兩個角度出發,判斷不同自變量所對應的函數值的大小關系.畫函數圖象要先求定義域,然后在定義域內找特殊點,比如,端點、斷點和極值點,并注意函數的圖象變化趨勢.
2 識圖
對于給定的函數圖象,要能從函數圖象的分布范圍、變化趨勢、對稱性等方面研究函數的定義域、值域、最大值、最小值等有關問題.
例2函數的圖象是( ).
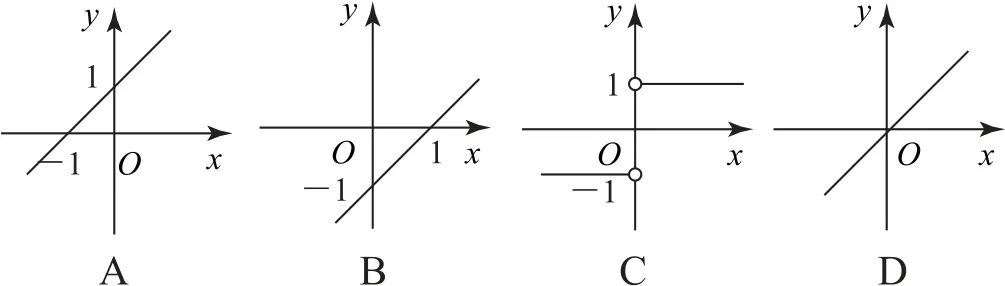
所給函數可化為

故對應的圖象為C.
其實本題也可以直接根據函數的定義域{x|x≠0},結合待選圖象的特征,加以準確識圖作出正確判斷.在解答這類問題時,關鍵是抓住題目相應的量與量之間的對應關系和變化規律,結合初等函數的相應規律進行分析與判斷.
3 用圖
函數圖象形象地顯示了函數的相關性質,為研究數量關系提供了“形”的直觀性,是探求解題途徑、獲得問題結果的重要工具.
例3設x∈R,求函數的最小值.
當0<x<1時,函數為反比例函數
圖象的一段;當x≥1時,函數為直線y=x圖象的一段.從而可得到函數圖象(如圖2),結合圖象可知,函數的最小值為1.

圖2
此類問題通過數形結合可以非常直觀明了地判斷對應的最值問題.要注意作圖的準確性,特別是端點和分段點的位置,只有保證作圖的準確性,才能準確用圖,為解題帶來方便.
高中數學中,作圖是函數的基本技能之一,通過作圖為識圖和用圖提供直觀依據,而識圖又可以更精確、更有目的地用圖.用好函數圖象是最高目標,可以用來求解函數值、函數定義域、值域等相關問題,也可以用來處理一些與函數性質有關的其他問題.

