交會成就精彩
——賞析定積分的交會命題

◇ 李 勇

定積分是新課標教材的新增內容，其基本思想是通過無限分割、近似替代、求和、取極限來達到計算的目的．在高考中，往往重點考查運用定積分的幾何意義、基本性質和微積分基本定理等進行積分計算．定積分的幾何意義是求曲邊圖形的面積，在高考試題或模擬試題中基本都是圍繞這一視角命題的．本文從定積分與其他知識的交會點出發，賞析其命題亮點．

1 與解析幾何的交會

例1已知拋物線W:y＝ax2經過點A(2，1)，過A作傾斜角互補的兩條不同直線l1，l2．

(1)求W的方程及準線方程；

(2)當l1與W相切時，求l2與W所圍成封閉區域的面積．

(1)由于A(2，1)在拋物線W:y＝ax2上，所

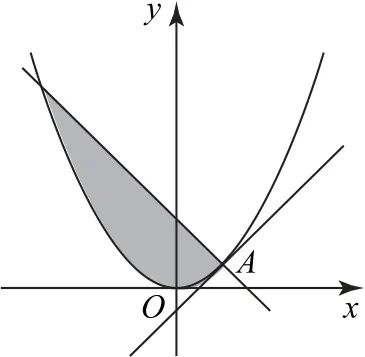
圖1

(2)當l1與W相切時，由y′|x＝2＝1，可知l1的斜率為1，所以l2的斜率為－1，所以l2的方程為y＝－x＋3，將其代入W的方程，得x2＋4x－12＝0，解得x1＝2，x2＝－6，所以l2與W圍成封閉區域的面積(如圖1中陰影所示)為

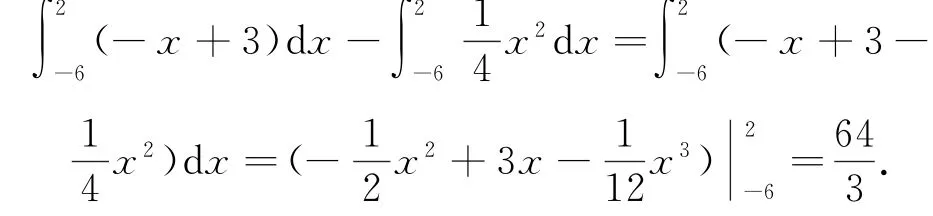
利用定積分的幾何意義求曲邊圖形的面積時，通常先在平面直角坐標系中畫出被積函數的圖象，再根據圖象確定積分的上、下限；最后運用微積分基本定理計算定積分．需要注意的是某些問題若選擇x作為積分變量求解較為煩瑣時，可以將y作為積分變量進行求解．

2 與概率的交會

例2圖2中的曲線是函數x≤π)的圖象，在長為2π、寬為2的矩形內，任意投一點，則該點落在陰影內的概率為( )．

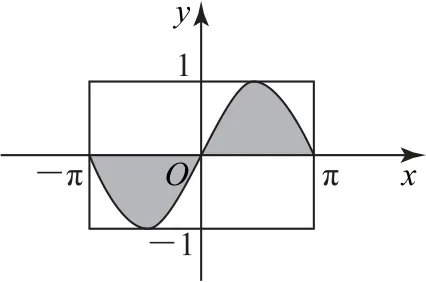
圖2

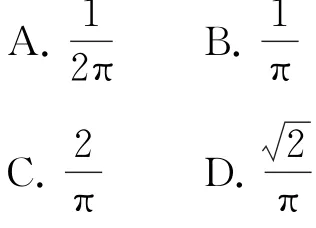
3 與不等式的交會

例3已知x．證明:

(1)當x＞0時，恒有g(x)≥f(x)；

(1)略；

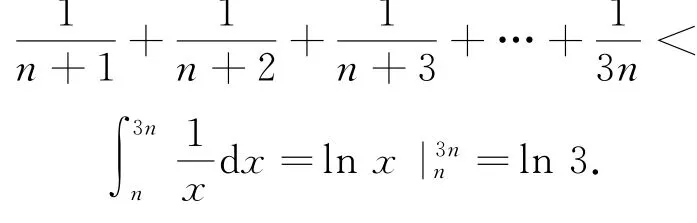
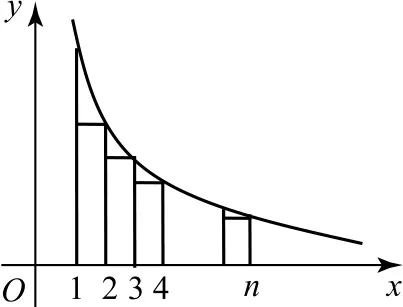
圖3

由圖4知，區間[n＋1，3n＋1]上的2n個矩形的面積之和大于該區間上的曲邊梯形的面積，即

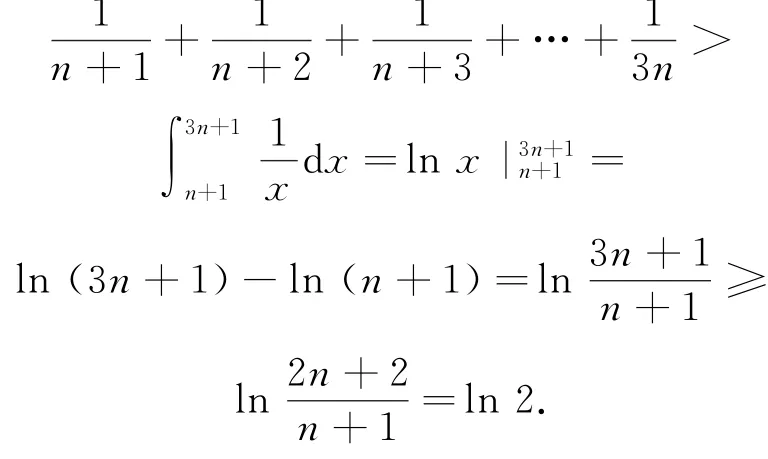
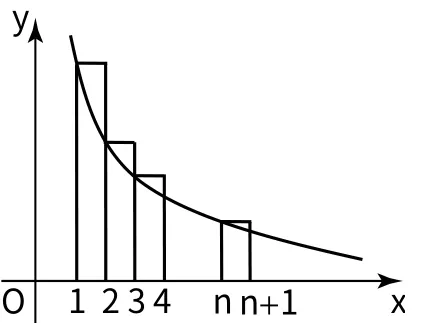
圖4

4 與其他學科的交會

例4行駛在平直的高速公路上的一輛汽車，由于遇到緊急情況而剎車，以速度v(t)＝7－3t＋25

1＋t(t的單位:s，v的單位:m·s－1)行駛至停止，在此期間汽車繼續行駛的距離(單位:m)是( )．

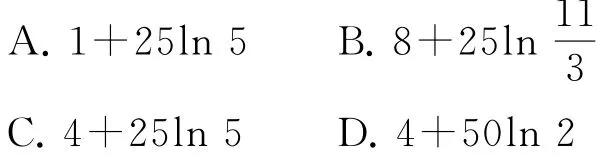
當汽車停止時，v(t)＝0，即0，解得t＝4或(舍去)．所以行駛的距離

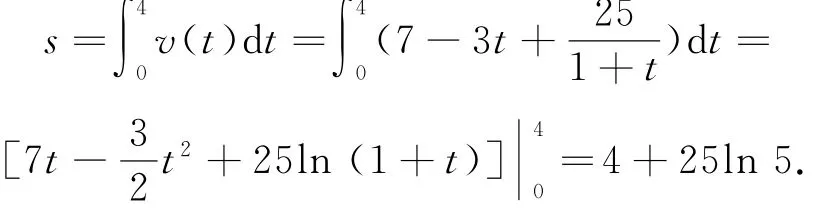
本題與物理中的變速直線運動相結合，考查了定積分的應用．定積分是研究數學、物理等問題的重要工具，它的引入，為解決中學數學、物理中的很多問題提供了簡單有效的方法．

除了本文所述的幾種典型的交會問題以外，還有定積分與向量、數列等的交會，問題常考常新，但只要我們正確把握定積分的幾何意義，準確計算，問題即可順利獲解．