走出定積分的幾個誤區
◇ 彭 暉
數學解題,必須謹防誤區,定積分問題也不例外.那么定積分問題中,有哪些誤區值得我們格外注意呢?為了讓學生防患于未然,筆者歸納如下,供讀者參考.
1 搞錯區間端點
定積分的計算體現無限分割、化整為零的思想,而分割后的每一個小區間必須表達準確.因為這是利用定義求定積分的前提,不可馬虎.
例1求由拋物線y=2x2與直線x=0,x=t(t>0),y=0所圍成的曲邊梯形的面積時,將區間[0,t]等分成n個小區間,則第i-1個區間為( ).

錯解因為從x=0到x=t得區間長度為t,平均分成n份,每個小區間長度為所以第i-1個區間為.故選C.
剖析將區間[0,1]等分成n個小區間,則第1個小區間左端點是0,第2個小區間左端點是依此類推,可知第i個小區間左端點是,因此將區間[0,t]n等分后,第i個小區間的左端點為
正解將區間[0,t]分成n個相等的小區間,每個小區間的長度為故第1個小區間為第2個小區間為第3個小區間為,故第i-1個區間的左端點為右端點為故選D.
這其實是一種容易出現的簡單計算錯誤,唯有仔細認真方可避免此類錯誤.
2 錯用定積分的幾何意義
定積分的幾何意義是求曲邊梯形的面積,但它的值卻有正有負,位于橫軸下方部分的定積分的值為負數,作為面積的值應化負為正,這一點也同樣不容忽視.
例2請用定積分表示由y=cosx和x軸在0與2π之間圍成的平面圖形的面積.
錯解根據曲邊梯形的面積計算和定積分的幾何意義,得所求面積為
剖析畫圖不難發現,所圍成的平面圖形,部分在x軸上方,部分在x軸下方,其定積分值有的為正,有的為負,但面積的值均為正,故求x軸下方的面積時,應將其積分值取絕對值.
正解所求面積的積分可分為三個部分,即[0,根據定積分的幾何意義,所求面積可表示為

當x∈[a,b]時,若f(x)<0,則由直線x=a,x=b,x軸和曲線f(x)圍成的圖形的面積應為
3 忽視積分變量
對于一個含參函數的積分,必須分清哪個變量是自變量,不可張冠李戴.避免此類錯誤,唯有認真審題,不可走馬觀花.
例3
錯解
剖析對于積分變量x來說,被積函數表達式f(x)=t2+t為常數,它與f(x)=x2+x是不同的.
正解
解決定積分問題時,審題時要注意五點:一要確定好積分變量;二要清楚積分上、下限;三要明確積分的幾何意義,區分積分與平面圖形面積的區別與聯系;四要會用導數尋找原函數;五要用好積分性質和微積分基本定理.只有這樣,才可保證計算不會出錯.
4 被積函數和積分上下限確定不準確
求曲邊梯形的面積,必須要確定所在的位置,也就是被積函數和積分的上限與下限,不可發生半點偏離,否則難保計算準確.
例4求由拋物線y2=8x(y>0)與直線x+y-6=0及y=0所圍成平面圖形的面積.
錯解由,得由x+y-6=0,得或舍去).故所求面積

剖析上述錯解在于沒有仔細分析圖形,導致被積函數搞錯,積分的上下限弄錯.
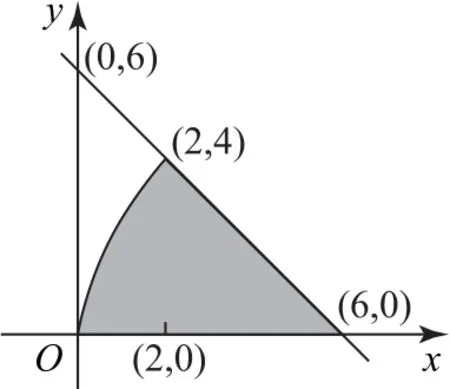
圖1
正解先作出所圍成平面圖形的示意圖,如圖1所示,由得于是得到拋物線y2=8x(y>0)與直線x+y-6=0的交點(2,4).
方法1(選y為積分變量)

方法2(選x為積分變量)

處理較復雜的平面圖形的面積,一般用定積分法,但應注意以下三點:
1)要根據圖形確定積分變量(選x還是y),并確定好積分上限和下限;
2)要依據積分變量確定被積函數,當積分變量為x時,將圍成平面圖形的上方曲線減去下方曲線,就是被積函數;當積分變量為y時,將圍成平面圖形的右方曲線減去左方曲線,就是被積函數;
3)要找準原函數.

