水電混合網絡經濟調度問題的分布式優化算法設計與分析

李 朋，胡江平，張榆平

(電子科技大學自動化工程學院 成都 611731)

Clean energy and water are two essential resources for the development of our society.Traditionally, the production of potable water and power generation are thought of as separable problems. However, with the development of technology, they are becoming increasingly correlated.For example, multi-stage flash (MSF) seawater desalination systems are usually coupled with power plants because they can use the wasted energy of used gas (which exits from gas turbine cycles) to produce potable water, while the gas turbine generator needs water to produce energy. With this scheme, it contributes to improving the fuel efficiency of the whole plant[1].

In recent years, a large number of researchers have investigated the energy-water nexus from various aspects. For example, Ref. [2] developed a model to save the energy and water by optimally controlling the lawn irrigation. Ref. [3] implemented an energy optimization model with a dedicated water module to assess an optimal “water-energy” mix. Ref. [4]developed a quantitative, physics-based model of the energy-water nexus to optimize the energy and water systems from an engineering system perspective. Ref. [5]developed a competitive Markov decision process model for the energy water-climate change nexus and the model was solved by a reinforcement learning algorithm. Ref. [6] established a multi-objective optimization model to study the room and realization path of both energy and water conservation under the prerequisite of stable economic development. Ref. [7]developed an integrated model analysis framework and tool to help predict and satisfy water, energy, and food demands based on model inputs representing productions costs, socioeconomic demands, and environmental controls. Although these research efforts are helpful for solving the energy-water nexus issues, most work adopts centralized methods to handle the associated optimization problem. It means that these approaches require a control center to acquire and process all the data from the whole network. As the scale of network becomes larger and larger, the control center can ’t bear so much computation burden.

To overcome the weakness of centralized method,various distributed algorithms have been developed for large-scale network optimization problem. For example, Ref. [8] proposed a distributed adaptive droop control method for DC micro-grid to optimize power dispatch. Ref. [9] designed a distributed method based on incremental cost for the conventional economic dispatch problem (EDP). Ref. [10] still adopted the equal incremental cost criterion to achieve the optimal dispatch, but the proposed algorithm can estimate the mismatch between demand and total power in a collective sense. Ref. [11] firstly used the logarithmic barrier function to reformulate the economic dispatch problem with capacity constraints and then employed the consensus approach to design the distributed algorithm. Ref. [12] proposed a distributed algorithm on the basis of projected gradient and finite-time average consensus algorithms for smart grid systems. Ref. [13] used the method of bisection and a consensus-like iterative method to solve the economic dispatch problem (EDP) in a smart grid.Ref. [14] proposed a distributed algorithm based on Laplacian-gradient dynamics for an EDP without and with capacities constraints. Then, Ref. [15] extended the initial strategy and presented the algorithm which could converge to the optimal solution of the dispatch problem starting from any initial power allocation in a distributed manner. Ref. [16] proposed an algorithm which is capable of solving the EDP in a minimum number of time steps instead of asymptotically.Ref. [17] employed the ADMM and finite-time algorithm to design a distributed algorithm for the EDP over the directed graph. Ref. [18] first designed a distributed inexact consensus-based ADMM method for the unconstrained optimization problem. Based on the work[18], Ref. [19] proposed a distributed inexact dual consensus ADMM to solve the EDP with complex structure object function. Ref. [20] provided two classes of continuous-time algorithms to solve the EDP in an initialization free and scalable manner by adopting either projection or differentiated projection method. Ref. [21] developed a distributed algorithm for the EDP with local non-smooth cost function over weight-balanced digraphs. Ref. [22] adopted a projected output feedback method to solve the EDP with uncertain parameters.

In this paper, we present a novel continuous-time distributed algorithm to solve the economic dispatch problem of the energy-water nexus with local inequality constraints in the framework of non-smooth analysis and algebraic graph theory. To the best of our knowledge, this is the first attempt to provide a quantitative solution for the economic dispatch problem of the energy-water nexus. Firstly, based on the exact penalty function method, we transform the original economic dispatch problem into an equivalent problem without local constraints. Then we propose a distributed algorithm to solve the equivalent problem in a distributed manner, which means that each plant or agent of the network only needs to obtain its neighbors’ information. Therefore, the proposed algorithm can be effectively applied to the large-scale water and power network. Compared with many existed algorithms which cannot get the correct optimal solution if the initial condition has an error,the proposed algorithm in this paper allows a group of plants to solve the economic dispatch problem for any initial value. Moreover, in our algorithm, we do not require the agents or plants to share their respective gradient information with their neighbors. In other words, the proposed algorithm can favorably protect plants’ privacy.

Notations: R and RNrepresent the set of real numbers and real N-dimensional column vector,respectively; 1N(or 0N) denotes an N-dimensional column vector whose all elements are 1(or 0); for a vector or a matrix x , xTrepresents its transpose, and ∥·∥represents the Euclidean norm of a vector or the corresponding induced norm of a matrix; inf(S)represents the greatest lower bound of the set S; A?B denotes the Kronecker product of the matrix A and B.

1 Preliminaries

In this section, some basic concepts about algebraic graph theory are firstly introduced. Then we review some notions from non-smooth analysis and differential inclusion. Finally, we formulate the economic dispatch problem of the energy water nexus.

1.1 Graph Theory

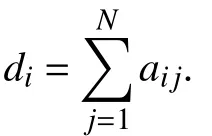
Assumption 1: The graph G=(V;E;A) is undirected and connected.

1.2 Non-smooth Analysis and Optimization

We recall some notions from non-smooth analysis[24]. A function f :RN→R is locally Lipschitz at x ∈RNif there exist positive constants ε and δ, such that for any vectors y,z ∈B(x,δ), one has|f(y)?f(z)|≤ε∥y?z∥. If f is Lipschitz near any point x ∈RN, then f is said to be locally Lipschitz in RN. If the function f is locally Lipschitz in RN, then f is differential almost everywhere (a.e.) in the sense of Lebesgue measure. The generalized directional derivative of f at x in the direction v ∈RNis defined,

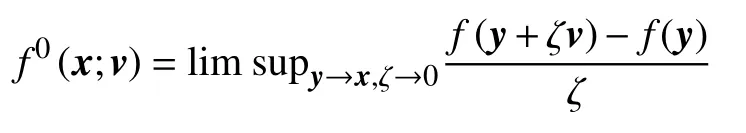
Furthermore, Clarke’s generalized gradient of f at x is defined by

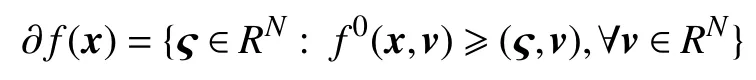
If f :RN→R is a convex function, then one knows that ?f(x) is a nonempty, convex, compact set of RN, and ?f(x) is upper semicontinuous at x.

A time-invariant differential inclusion is given by

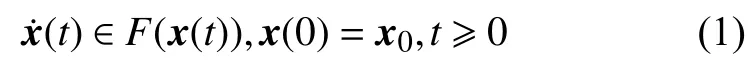
where F is a set-valued map from Rqto the compact convex subsets of Rq. A solution x(t):(0,τ)→ Rqfor τ>0 of the differential inclusion (1) is an absolutely continuous curve almost everywhere. A set M is said to be weakly invariant (resp., strongly invariant) with respect to (1), if for every x0∈M , M contains at least a solution (resp., all the solutions) of (1) starting from x0. An equilibrium point of (1) is a point xe∈Rqwith 0q∈F(xe). An equilibrium point z ∈Rqof (1) is Lyapunov stable if, for every ε>0, there exists δ=δ(ε)>0 such that, for every initial condition x0=x(0)∈B(z;δ), every solution x(t)∈B(z;δ) for all t>0.

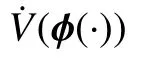
Lemma 1: For the differential inclusion (1),assume that F is upper semicontinuous and locally bounded, and F(x) takes nonempty, compact, and convex values. Let V:Rq→R be a locally Lipschitz and regular function, S ?Rqbe compact and strongly invariant for (1), ?(·) be a solution of (1),

X={x ∈Rq:0 ∈LFV(x)}

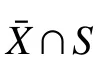
1.3 Problem Formulation

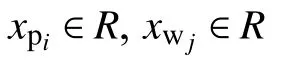
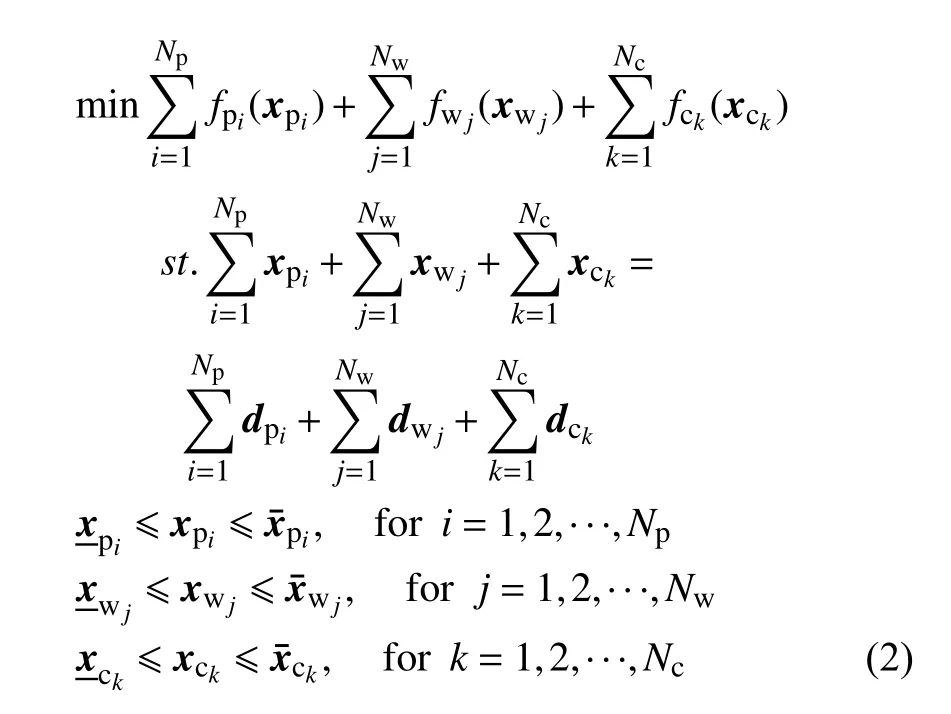
Remark 1: The equality constraint is a global constraint which denotes the supply-demand balance while the inequality constraints represent the reasonable limits of plants’ production capacity.

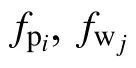
2 Distributed Algorithm Design

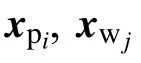
where

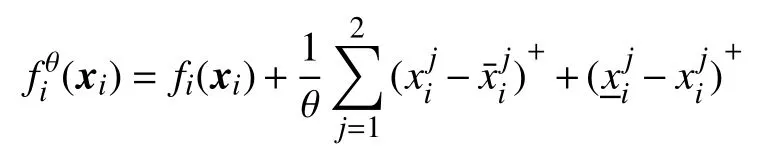
Lemma 2[14]: The solutions to the optimization problems (2) and (3) coincide for θ>0 when

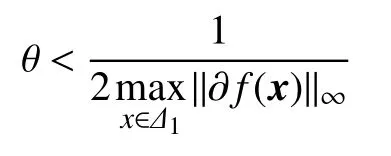
where

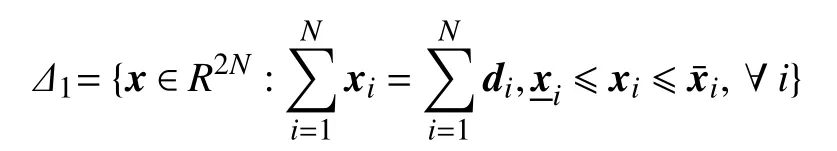
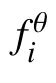
Now, a distributed algorithm is provided to solve the problem (3)

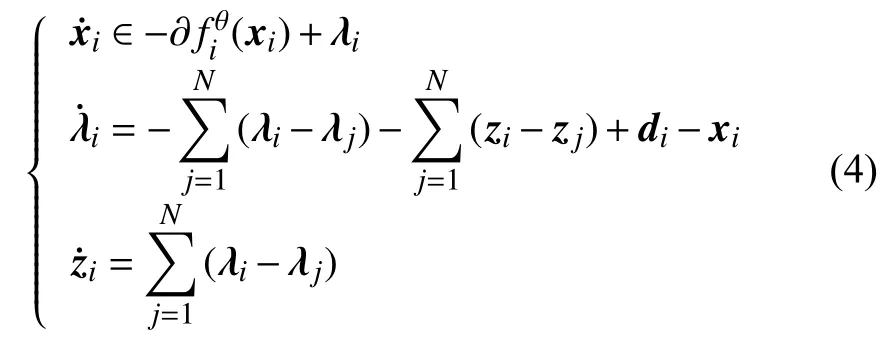
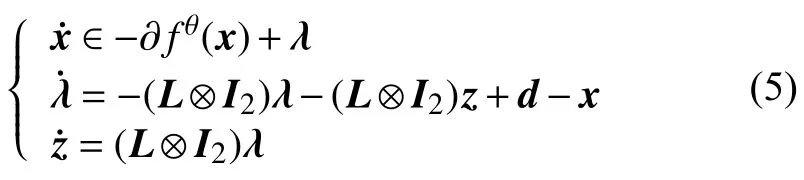
Theorem 1: Under assumption 1 and assumption 2, if (x?,λ?,z?) is an equilibrium point of the distributed algorithm (5), then x?is an optimal solution of the problem (3).

Proof: Since (x?,λ?,z?) is an equilibrium point of the algorithm (5), then one has,

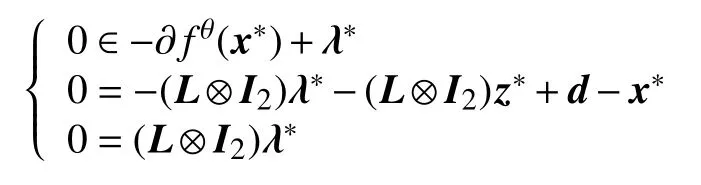
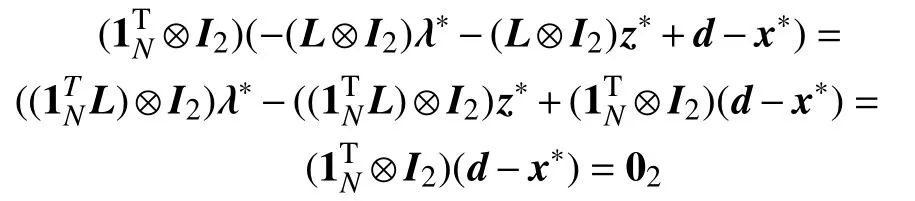
Therefore, the equilibrium point (x?,λ?,z?) of the algorithm (5) satisfies

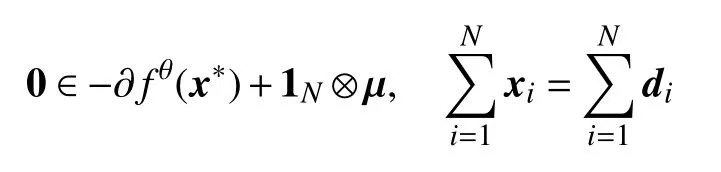
which is exactly the optimal condition for problem (3).Thus, the equilibrium point x?is the optimal solution of the problem (3). The proof is completed.

Remark 2: From Theorem 1, it is sufficient to show that the algorithm (5) can converge to the optimal solution x?if the algorithm (5) converges to the equilibrium point (x?,λ?,z?). Next, we show that the algorithm (5) converges to the equilibrium point.

Theorem 2: For any initial state, the solutions of the algorithm (5) converge to the equilibrium point(x?,λ?,z?) under assumption 1 and assumption 2.

Proof: Define an energy function

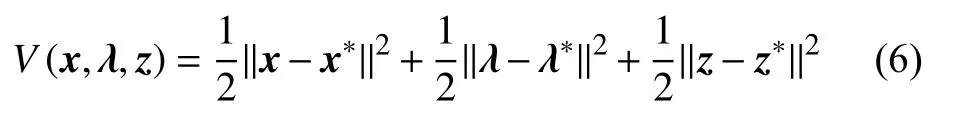
It is noted that there exists a vector g ∈?fθ(x) such that

LFV(x,λ,z)=(x?x?)T(?g+λ)+(z?z?)T(L?I2)λ+(λ?λ?)T[?(L?I2)λ?(L?I2)z+d ?x]=?(x?x?)T(g?g?)?(λ?λ?)T(L?I2)(λ?λ?)

for any g ∈?fθ(x). Since fθ(x) is convex and the Laplacian matrix is positive semidefinite, one has

?(x?x?)T(g?g?)?(λ?λ?)T(L?I2)(λ?λ?)≤0

Thus, maxLFV(x,λ,z)≤0 and V(x(t),λ(t),z(t)) is nonincreasing. It is easy to obtain that

V(x(t),λ(t),z(t))≤V(x(0),λ(0),z(0))Furthermore, the solution (x(t),λ(t),z(t)) is bounded.Then we know that

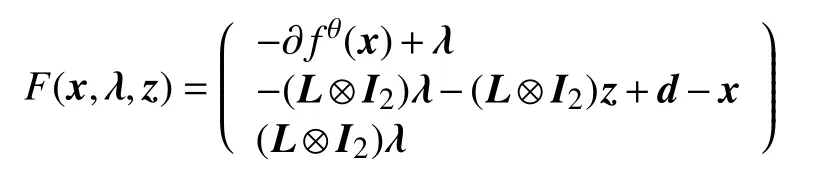
is upper semicontinuous and locally bounded. At the same time, the energy function V(x,λ,z) is a locally Lipschitz and regular function. Let S ={(x,λ,z):0 ∈LFV(x,λ,z)}. Since LFV(x,λ,z)≤0, S is a compact and strongly invariant set for the algorithm (5). Thus,according to Lemma 1, the solution of the algorithm(5) starting from any initial value converges to the largest weakly positively invariant set M.

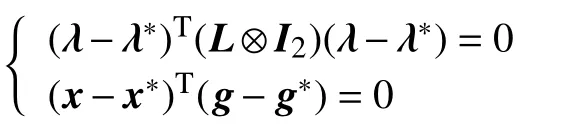
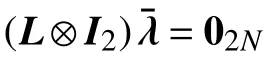
(x?x?)T(g?g?)=(x?x?)TH(τx+(1?τ)x?)(x?x?)

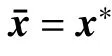
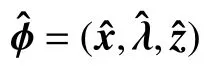
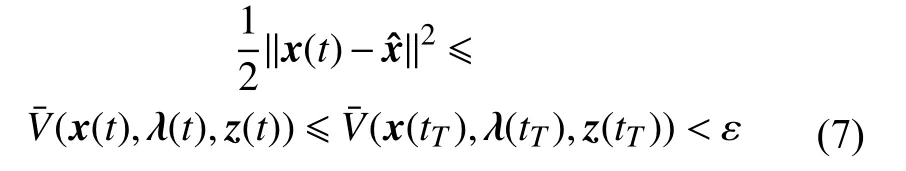
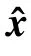
Remark 3: It is noted that the algorithm (4) is a differential inclusion and implemented by using only the plant’s neighbors information. The gradient information is not shared in the neighborhood and thus the proposed algorithm can favorably protect the privacy of agents.

3 Simulation

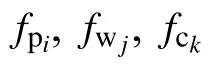
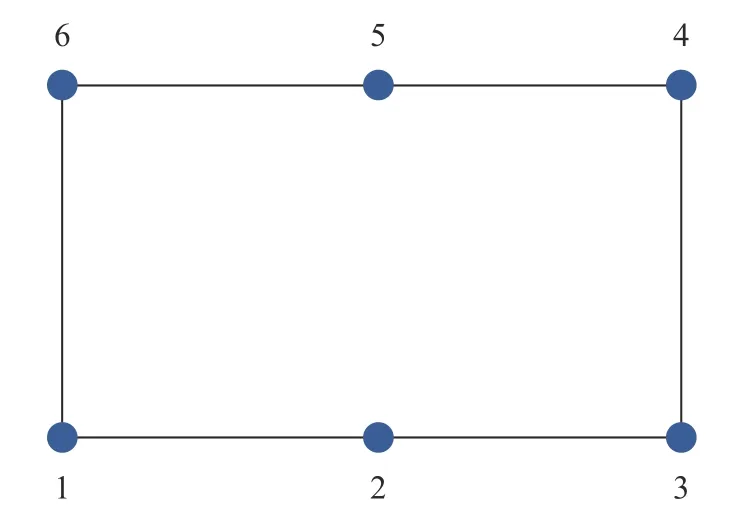
Fig.1 The communication network

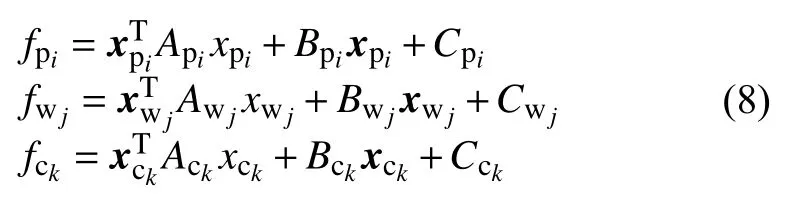
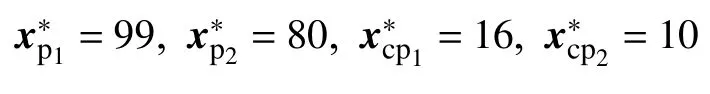
Table 1 The parameters of the plants

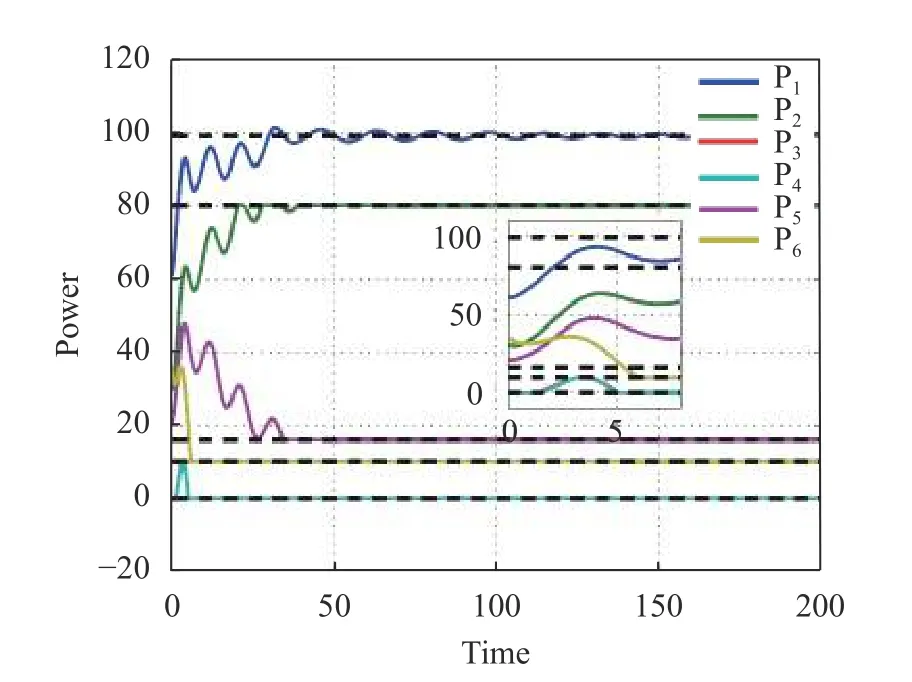
Fig.2 The evolution of power allocation

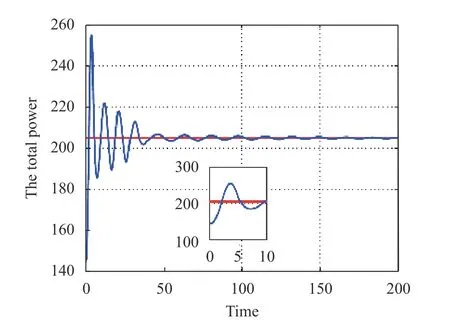
Fig.4 Total mismatch of power

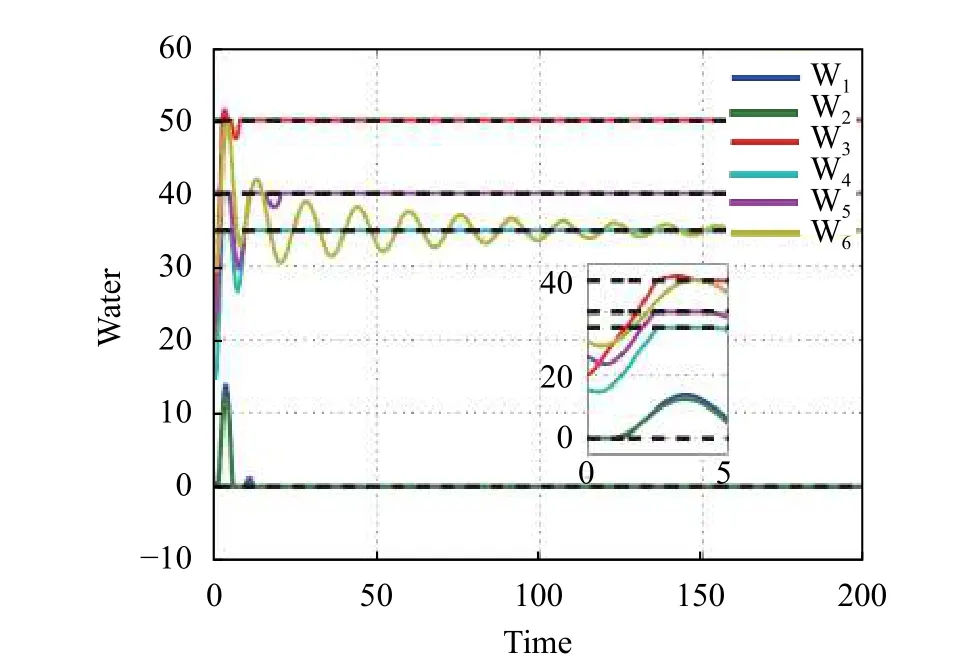
Fig.3 The evolution of water allocation

4 Conclusions

In this paper, we have designed a distributed continuous-time algorithm which allows a group of power, water, and coproduction plants to solve the economic dispatch problem with local inequality constraints starting from any initial allocation. To accomplish this, we have transformed the original problem by using the exact penalty function method into an equivalent problem without local inequality constraints. Then a distributed algorithm has been proposed to solve the equivalent optimization problem.A theoretical analysis has been presented for the proposed algorithm with the help of algebraic graph theory, Lyapunove function method, and non-smooth analysis. The simulation result indicates that the algorithm is effective and it will save plenty of production cost for the economic dispatch problem of energy-water nexus. In the future, we will further investigate the economic dispatch problem of the energy-water nexus system which not only includes the electricity-storage devices but also the water storage facilities. Moreover, we will consider the power-water production ratio for the coproduction plants in the co-optimization model such that the model is more practical.