交叉路口基于車輛權值分簇的中繼轉發方案

肖海林，毛淑霞，王慶菊

(1. 桂林電子科技大學信息與通信學院 廣西 桂林 541004；2. 湖北大學計算機與信息工程學院 武漢 430062；3. 溫州大學計算機與人工智能學院 浙江 溫州 325035)

車輛自組網(VANETs)是智能交通系統的核心，能夠為駕駛員提供實時的交通誘導、安全及娛樂等信息，低時延、高可靠性通信是VANET 的關鍵。然而，車輛的移動特性使得VANET 的動態拓撲結構快速變化，故無法滿足穩定性的通信需求。將分簇方法應用于車聯網中，可以降低通信的不穩定性和復雜性。通過簇頭車輛進行信息傳輸，可以提高交通效率，降低傳輸時延。目前，大多數的分簇方法是針對簡單的多車道公路場景進行設計的[1]。如，文獻[2]利用較低的傳輸延遲和網絡開銷獲得較高的傳輸成功率，對停放路邊和非路邊車輛進行分簇。文獻[3]考慮雙向車道信息共享，提出基于時間劃分策略和基于最優長度的分簇機制。在交叉路口，車輛會出現聚集現象，車輛的連通率會提高，但車道上每個車輛的轉向不一致，車輛經過交叉路口后，簇的穩定性降低。為此，文獻[4]對通過交叉路口前的車輛行為進行預測，考慮車道數，從車輛數量最多的車道方向選擇簇頭。文獻[5]針對交通流不確定性對交叉口交通狀態的影響，提出一種基于區間數據的k均值聚類城市交叉口交通狀態識別方法。文獻[6]提出一種自適應分簇協議，考慮車輛節點的編號、方向、速度大小及鄰居車輛節點數目，采用多目標螢火蟲算法得到最優簇頭。

雖然簇的引入能提高車輛之間通信的穩定性，但以上文獻未考慮選擇有效的中繼轉發方式，以提高通信的可靠性[7]。基于傳統的放大轉發(amplifyforward, AF)和譯碼轉發(decode-forward, DF)[8]方式，文獻[9]采用單向混合譯碼放大轉發(hybrid decode-amplify-forward, HDAF)協作方式，比AF和DF 節約資源的消耗。文獻[10]在VANETs系統中采用雙向中繼協作方式，以實現兩源節點的雙向信息交流，在低功耗的情況下獲得高吞吐量。文獻[11]針對頻譜共享問題，對雙向中繼的選擇和頻譜分配進行優化，使網絡速率最大化。文獻[12]結合馬爾可夫決策過程，采用雙向中繼傳輸模式，推導網絡最優傳輸性能。以上文獻均使用瑞利衰落信道模型。但在實際復雜的衰落環境中，NaKagami-m 衰落信道模型更能體現出實際信道的衰落特性。為此，文獻[13]驗證了該衰落模型在車輛通信的適用性。在此基礎上，基于傳統AF/DF，通過最小化系統中斷來提高平均頻譜效率[14-15]。

綜上所述，本文在NaKagami-m 衰落信道條件下提出交叉路口的基于車輛權值分簇的中繼轉發方案。該方案包括簇的形成、簇頭的選舉、簇的維護及中繼轉發方式的選擇。

1 系統模型

如圖1 所示，考慮城市道路的交叉路口場景，假設交叉路口的每條道路是雙車道。交叉路口的轉向最多有3 個方向：左轉、直行和右轉。

由于在交叉口附近或者在車輛行駛的高峰期，車輛的速度和車輛之間的距離會相對穩定，變動的范圍不會過大，對車輛之間的傳輸性能影響較小，為了簡便算法可以忽略不計。由于城市道路上車流量是在不斷變動的，車輛在通信過程中會產生反射、繞射和衍射等現象，這些現象導致接收車輛會收到多條不同路徑到達的信號，而NaKagami-m 衰落更能體現出實際信道的衰落特性，故本文考慮NaKagami-m 衰落信道以表征車輛的通信信道[13]。車輛之間的交通流、相對距離以及連通率表示如下。

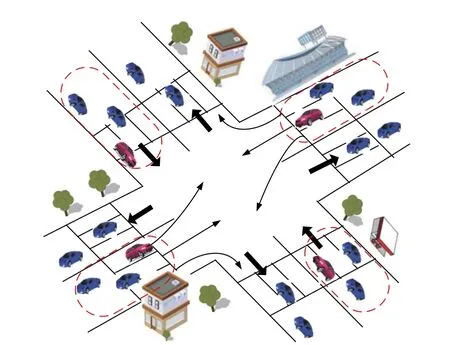
圖1 車輛分簇模型

1)交通流

在直線公路上，車輛數服從泊松分布，設公路長度為l ，車輛的平均密度為ρ(車輛數/m)，那么總的車輛數為λ=ρl，且公路上有 N輛車的概率為：

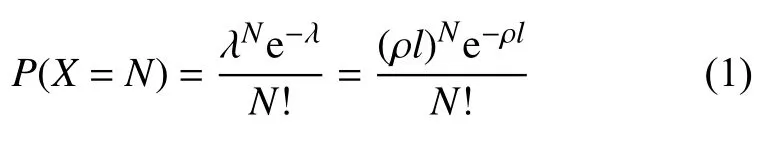
車輛在距離交叉路口處選擇行駛方向，左轉、右轉和前行，即可用一個有限集合k表示[16]：

k={L,R,S}，其中， L表示左轉， R表示右轉，S表示前行。

根據車輛的移動特性，對于不同車流量方向，車輛的權重不一樣，權重公式為：

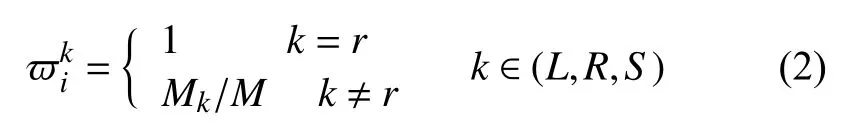
式中，在距離交叉口處的公路上，M(M ≤N)為車輛數； ML為左轉方向的車輛數； MR為右轉方向的車輛數； MS直行為方向的車輛數； r為車輛i的方向。

2)相對距離和速度

車輛在直線公路上，車輛是不分左轉、右轉和前行的，則車輛i的位置(xi,yi)與其鄰居之間總的相對距離和為：

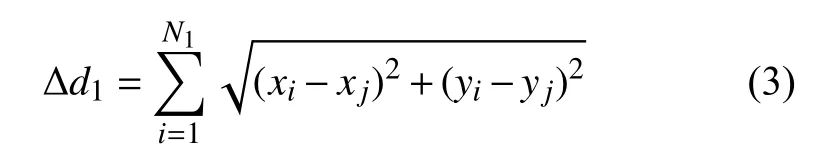
式中， N1為車輛i的鄰居數。

車輛i的速度 vi與其相鄰車輛的相對速度和為：

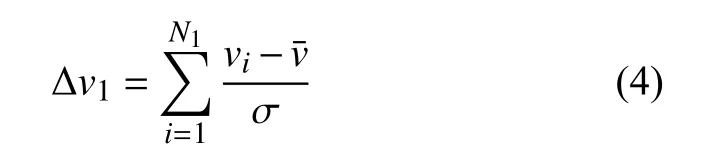
3)連通率

連通率[17]代表兩通信車輛間的鏈路質量，連通率越高，通信車輛間鏈路越穩定。設車輛i為簇頭車輛，通信范圍為 R，車輛i與鄰居車輛j之間的距離x服 從指數分布，車輛密度為ρ，均值為1 /ρ，方差為1/ρ2，則通信車輛間的概率密度函數為f(x)=ρe?ρx，兩車輛間連通的概率為px(x ≤R)=1?e?ρx，則車輛i的鄰居車輛共有 N1輛車的連通概率為：

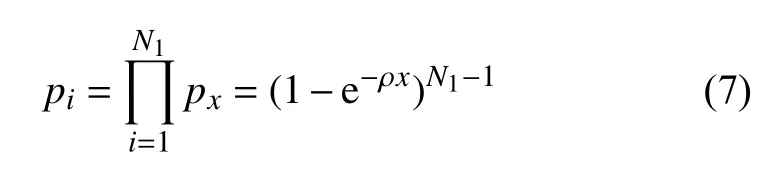
2 車輛權值分簇的中繼轉發方案

車輛在成簇的過程中受到多方面的影響，本文提出權值分簇算法選取各方向的最小權值作為簇頭，為提高通信的可靠性采用雙向AF/DF 的中繼轉發方式進行數據傳輸。

2.1 權值分簇算法

2.1.1 簇的形成

車輛可以選擇3 個方向通過交叉路口：前行、左轉和右轉。在車輛選擇方向時，車輛會自覺的排列到要轉同方向的隊伍中，形成通信簇。

2.1.2 簇頭的選擇

車輛i 在交叉口處開始向簇頭(CH)車輛發送車輛的信息，包括速度、到交叉口的距離，通過交叉口的轉向等。CH 之間每隔一段時間進行一次信息交換，每個CH 車輛接收到其簇成員(CM)的信息，在CH 信息交換后，把其他簇的信息通知到其CM。C1 為簇1，CH1 為簇1 內的CH 車輛；CM1 為簇1 內的CM。

圖2 為向右行駛車道上車輛分簇模型，C1 內有6 輛車，中間一排靠前的淡藍色車輛為簇頭CM1，通過CH1 知道其他簇的信息，同時CH1 把該簇內前行、向左和向右行駛的CM1 車輛信息發送給相應方向的CH1 車輛。C2 其他向前行駛車輛形成的簇，擁有與C1 簇相同的方式傳遞信息，該簇中向前、左轉和右轉的信息分別傳到對應最前邊(靠近交叉口)對應簇中，C3 為左轉車輛簇，C4 為前行車輛簇，C5 為右轉車輛簇。其中C2～C5 中綠色車輛為簇頭。

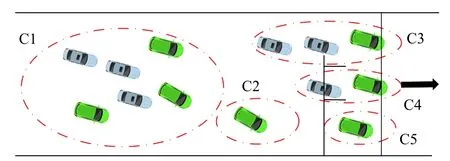
圖2 向右行駛車道上車輛分簇模型

C3～C5 中為不同方向的車輛簇，在接近交叉口處的直線車道上，CH 開始收集簇內其他車輛預行駛方向的信息，并把同一方向合成一個簇。

在每個簇內，采用多因子權值法，選出最優權值作為簇頭。在直線的道路上，簇頭的選擇公式為：

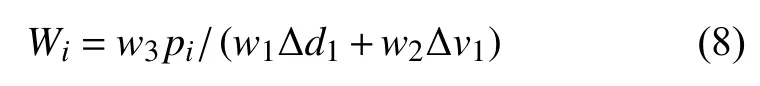
式中， w1為距離的權重；w1?d1表示距離的影響程度； w2為相對速度的權重；w2?v1表示速度的影響程度； w3為交通流的權重因子；w3pi表示連通概率的影響程度。并將3 個因素看成一個整體，即w1+w2+w3=1。對式(8)求得的各用戶綜合權重值進行升序排序，將排序靠前的最小值用戶作為簇頭。

由于交叉口處的車輛比直線道路上多，且一個簇內的車輛在交叉路口會有大幅度的調整，簇內許多車輛的運行方向不同，很容易造成簇的分離。所以，本文在交叉路口附近車輛進行不同方向的運動前，把直線道路上距離交叉路口近且不是簇內的車輛，根據預備相同轉向車輛分為一簇，并從中提前選好簇頭。同理，根據相同轉向車輛的相對距離及速度的影響程度，選擇綜合權重最小值作為簇頭，公式為：

2.1.3 簇的維護

根據元胞自動機模型[18]預測兩車輛間的距離，車輛i與車輛j在t時刻的初始位置為Xi(t)和xj(t)，速度和加速度分別為vi(t)、vj(t)和 ai、aj(當a>0為加速，a<0為減速)，在t+1時刻車輛i和車輛j的速度為：

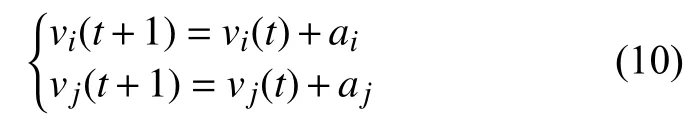
車輛的速度范圍在0～vmax。

t+1時刻兩車間的速度差為：

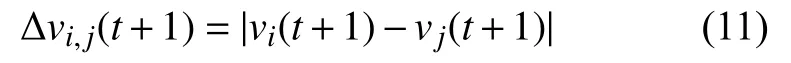
t+1時刻兩車間的距離差為：

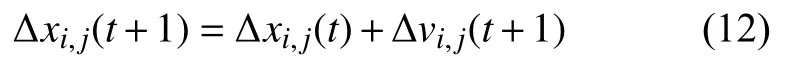
式中，?xi,j(t)=|xi(t)?xj(t)|

圖3 中紅色圓表示簇頭車輛，黑色圓表示簇成員車輛。

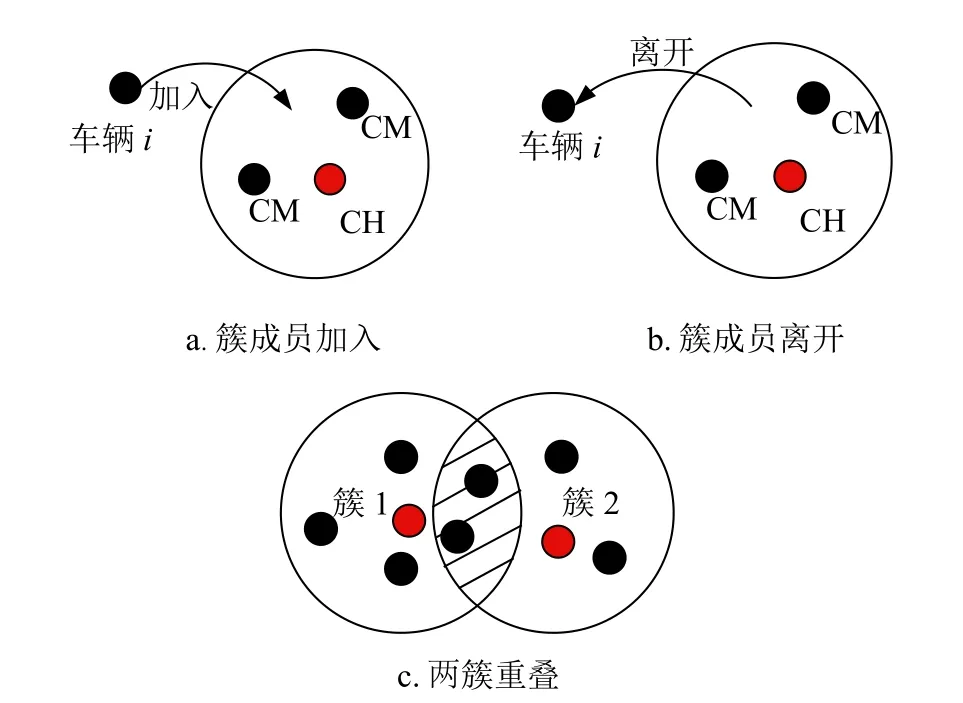
圖3 簇成員加入、離開及兩簇重合

1)簇成員加入

①車輛i 向四周發送信號，若收到一個簇頭車輛的回復，則加入該簇內；

②若收到大于一個簇頭車輛的回復，則比較此車輛與各簇頭車輛的預測距離，選擇距離近的簇頭并加入該簇內，簇頭更新成員列表，并通知其他簇成員此車輛加入該簇；

③若在 T 時間內，沒有收到任何簇頭的消息，則在其鄰居范圍內查看是否有鄰居簇成員，且在鄰居簇成員的通信范圍內。若在其通信范圍內，則加入簇，成為簇外成員，若不在通信范圍內，則繼續向四周發送信號，在 T時間內仍未收到任何簇頭或鄰居簇成員信息，則自己成為簇頭，如圖3a 所示。

2)簇成員離開

車輛從某個簇內離開之前，先向四周發送hello消息，若在 T時間內未收到任何消息，車輛向簇頭發送離開信息，并繼續向四周發送hello 消息，T1時間后，收到簇頭消息，加入簇，未收到消息自己成為臨時簇頭；若在 T時間內收到其他簇頭消息，車輛先向自己所在簇的簇頭發送離開信息，收到其他簇頭的信息，直接加入簇，收到大于一個簇首信息，按照預測距離小的，加入簇，如圖3b 所示。

3)兩簇重疊

當車輛在行駛的過程中，簇1 與簇2 之間的簇成員重疊的部分小于等于簇1(或簇2)成員的一半，則保持原狀；若大于簇1(或簇2)的一半，則重新分簇，只比較兩個簇頭的 W 值，選取 W值小的作為新的簇頭，如圖3c 所示。

2.2 雙向中繼轉發的中斷概率分析

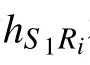
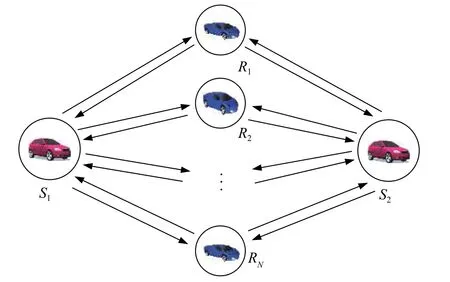
圖4 雙向中繼傳輸的系統模型

2.2.1 雙向AF 放大轉發

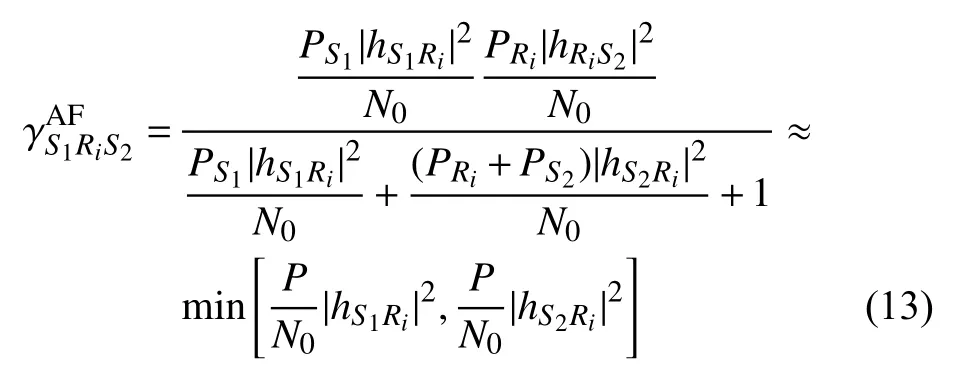
S1信號接收到經過第i條中繼信噪比近似為[19]：

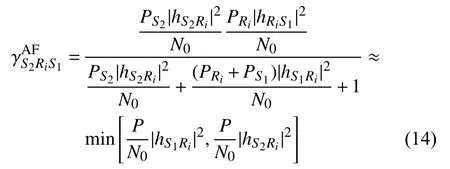
S1S2和 信號接收到的信息量分別為：

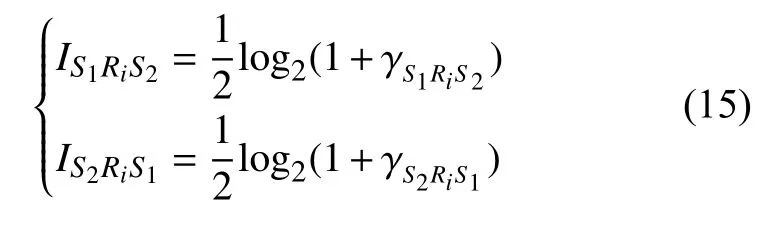
假設各信道幅度服從NaKagami-m 分布，且相互獨立。隨著 m參數的改變，NaKagami-m 分布能夠建模多種衰落特性的信道，當m=0.5時，NaKagami-m 分布變成單側高斯分布，當m=1時，變成瑞利分布。在NaKagami-m 信道下，節點i到節點j 的信道功率增益 gij服從Gamma 分布，其概率密度函數和累計分布函數可以分別表示為[20]：

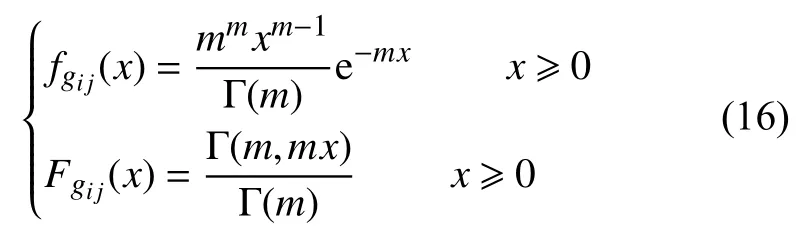
式中，Γ(a,ax)為不完全Gamma 函數；Γ(a)為完全Gamma 函數。

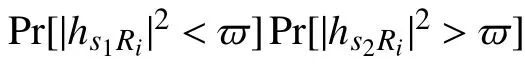
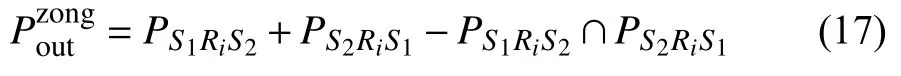
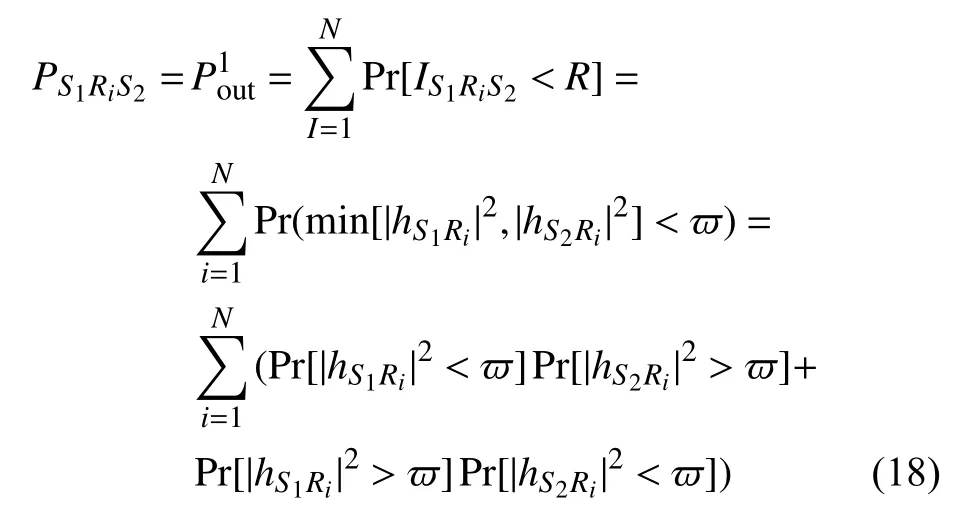
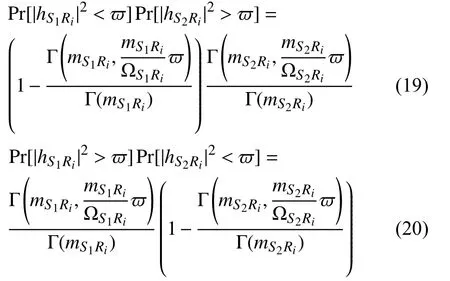
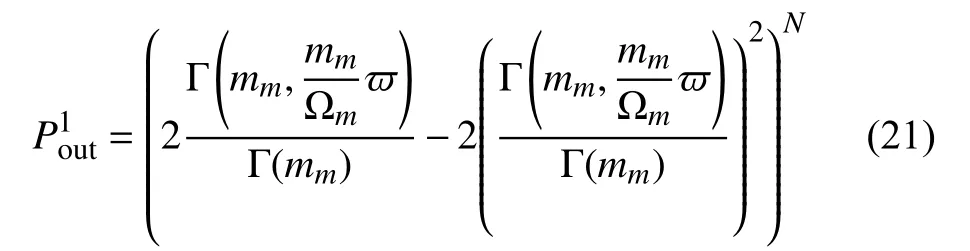
同理， S2信號傳遞給 S1時的中斷概率為：

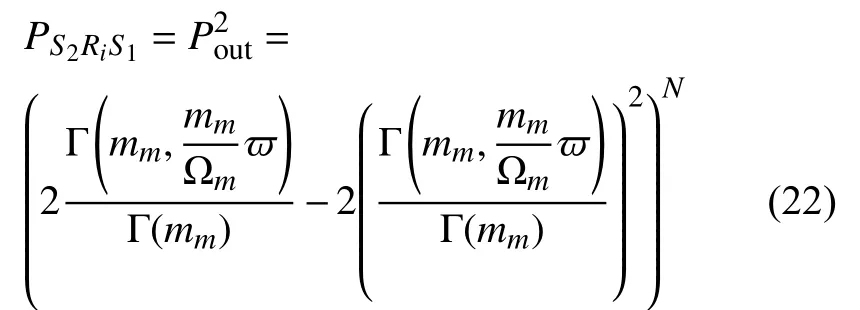
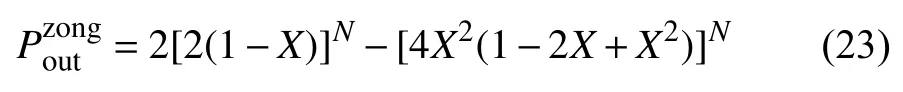
2.2.2 雙向DF 譯碼轉發

若采用DF 進行轉發，則S1→Ri、S2→Ri、Ri→S2、Ri→S1信噪比分別為：

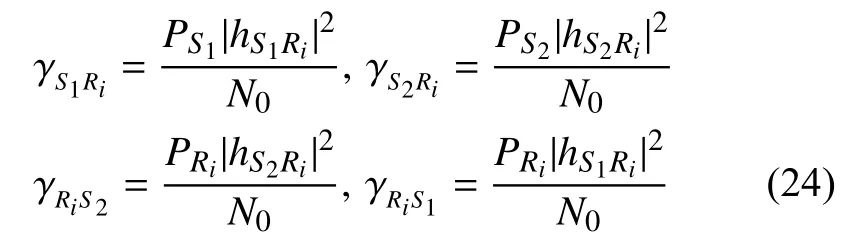
假設選擇中繼 Ri轉發信息，且所有信道在信息傳輸時間段保持不變。 Ri分別向兩個源節點傳遞信息的信息量為：

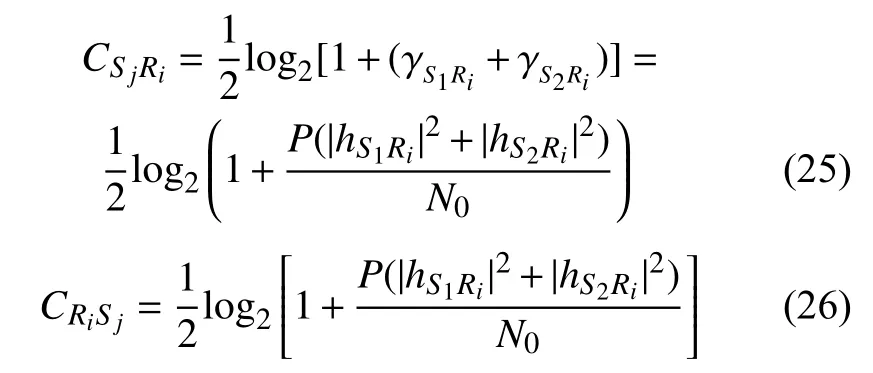
式中，j=1,2。

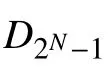
Φ=?時，

Φ=Dn時，

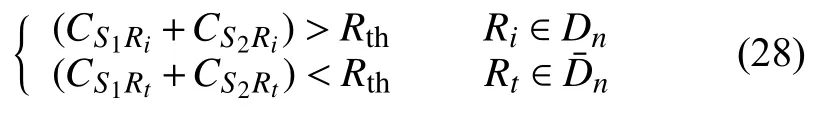
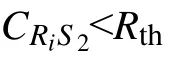
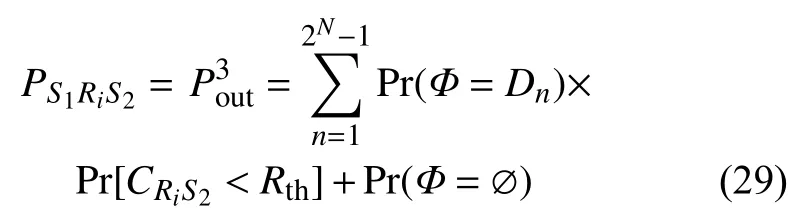
式中，Pr(Φ=Dn)的概率為：

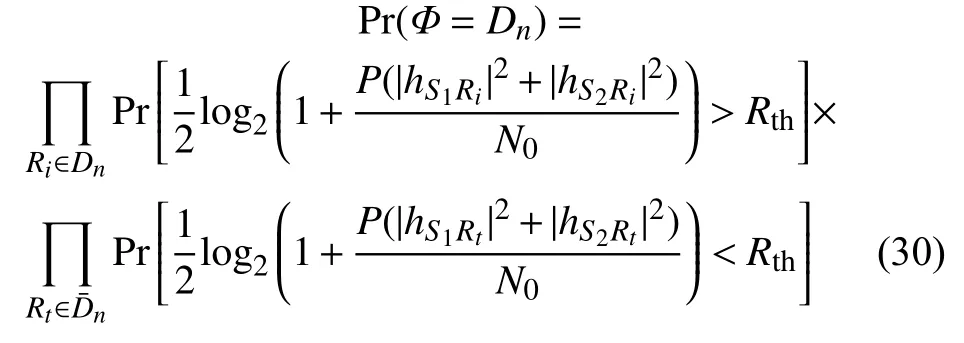
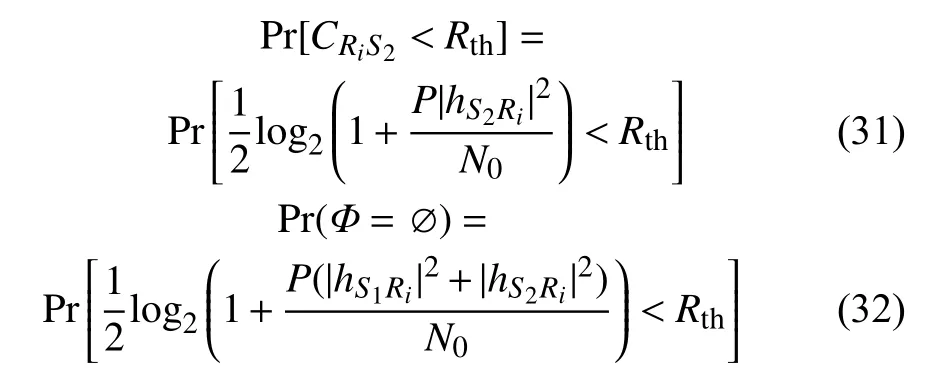
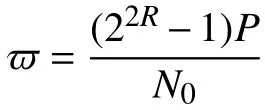
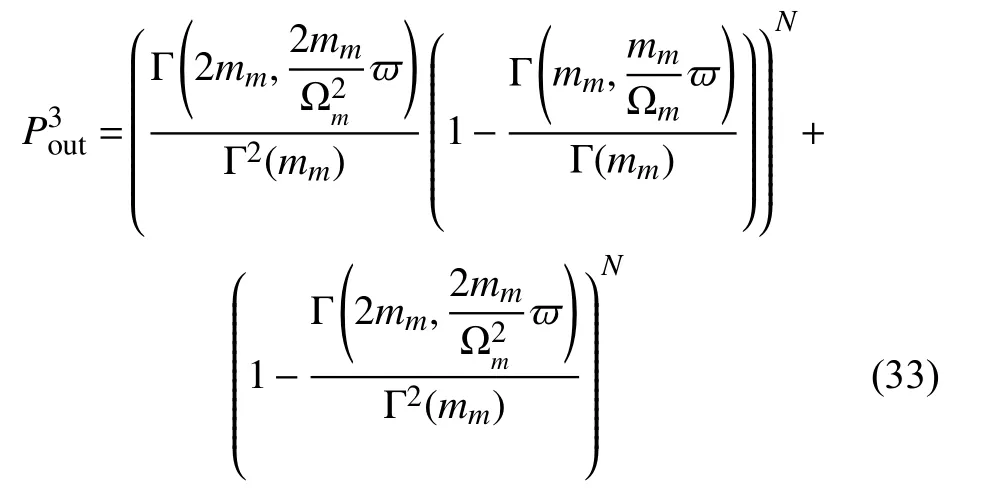
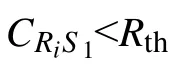
最后，令式(34) =Y，把式(33)與式(34)代入系統總中斷式(17)，有：

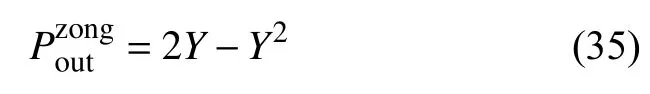
3 數值分析

本節主要從隨著通信距離的增加，CH 車輛的存活時間以及不同的中繼轉發、中繼個數和信道來判斷信噪比對中斷概率的影響。參數設置如表1 所示。

表1 參數設置

圖5 為不同車輛密度下傳輸半徑與連通率的關系。由圖可以看出，隨著傳輸半徑的增大，車輛的連通率增大，車輛有機會選擇不同簇頭，傳輸穩定性得到滿足。且車輛密度越大，連通率越大。

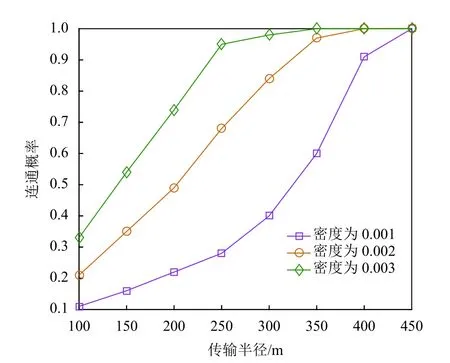
圖5 不同車輛密度下傳輸半徑與連通率的關系

圖6 為簇頭的存活時間。在車道上設置為60 輛/km 行駛的車流量密度，從圖中可以看出，與基于車道的分簇算法(lane based clustering algorithm,LBC)相比，趨于穩定狀態的時間提前了8 s，通信距離在不斷增加，相應簇頭存活時間就會相應變長。其原因是簇頭車輛的覆蓋面積變大，簇內的成員變多，當有車輛加入簇或者離開簇時，對簇的影響將減小。

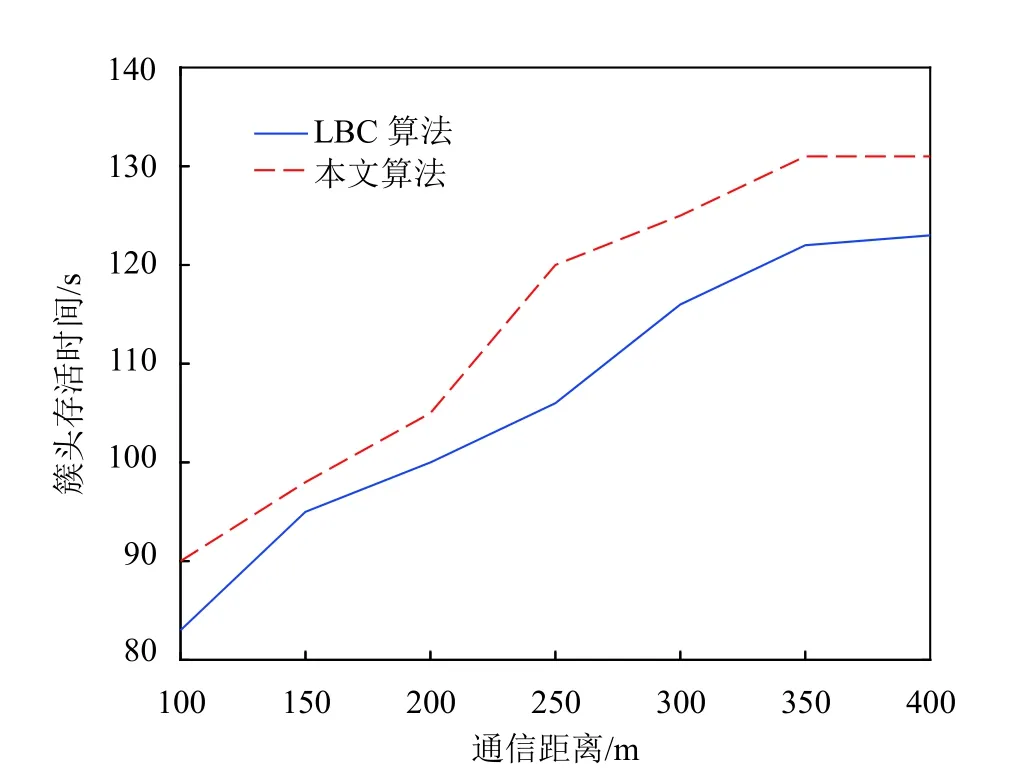
圖6 簇頭的存活時間

圖7 為不同中繼選擇下的中斷性能。在Nakagami-m 信道下且信噪比的范圍設置為0～16 dB，設m=1，中繼個數N=3。從圖中可以看出，在一定的范圍內，隨著信噪比的增加，雙向AF 和DF 的中斷概率要優于單向AF 和DF 的中斷概率。這是由于，單向中繼傳輸只能將源節點的信號傳遞單個目的節點，而雙向中繼傳輸是兩個源節點的信息同時傳遞給對方，會減少傳輸時間，降低中斷概率。

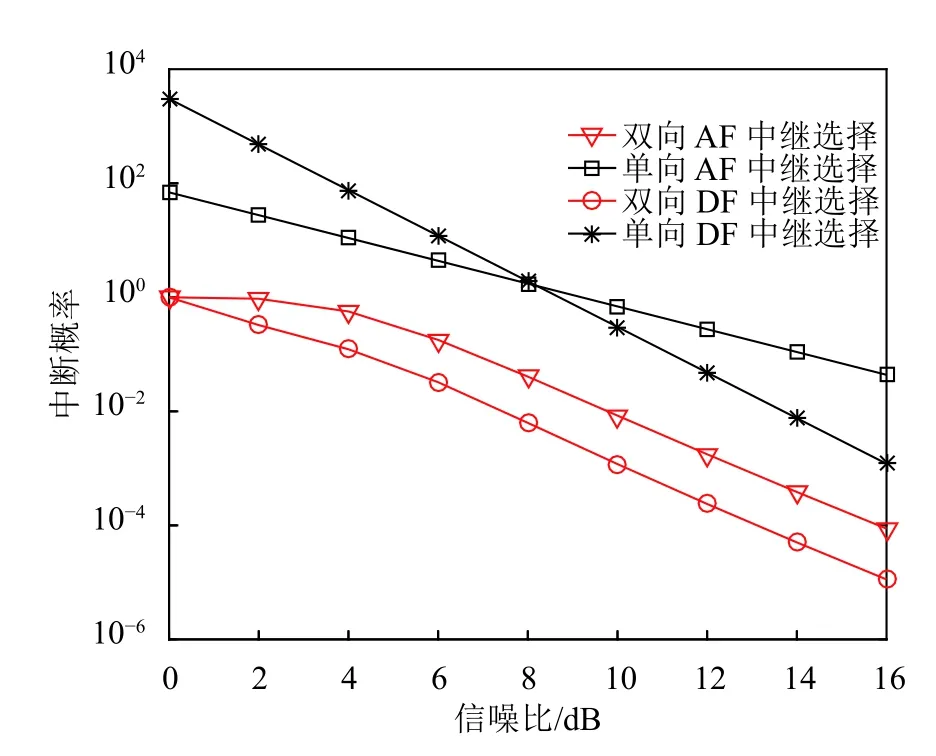
圖7 不同中繼選擇下中斷性能

圖8 為不同中繼個數對雙向中繼的影響。設m=1，中繼個數分別為2、4、6，信噪比的范圍設置為10～30 dB。由理論分析得出，當 N增加時，成功放大轉發和解碼的幾率就會增加，中斷概率會隨之降低，在相同中繼個數時，雙向DF 中繼要優于雙向AF 中繼，且圖8 的數值模擬與所分析的結論符合。

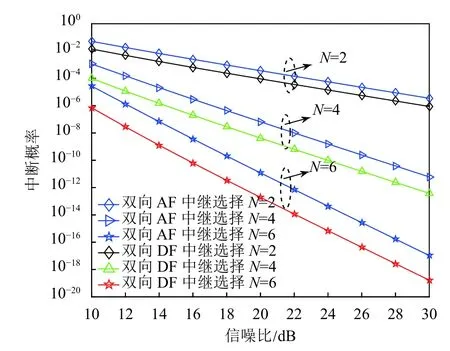
圖8 不同中繼個數對雙向中繼的影響

圖9 為不同 m值 下對中斷概率的影響。設N=3，Nakagami 信道衰落因子分別為0.5、1 和2。由理論分析可知，由m=0.5時的單側高斯分布到m=∞時的無衰落，隨著 m的增加，信道的衰落逐漸降低。圖9 的仿真模擬與理論分析相符合，隨著信噪比與 m的增加，中斷概率降低，傳輸速率增加。

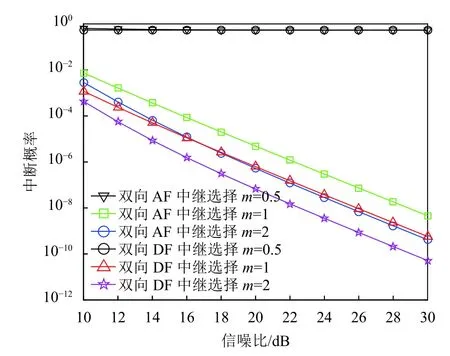
圖9 不同m 值下對中斷概率的影響

4 結 束 語

在城市交叉路口的場景下，為提高鏈路的穩定性及增強通信的可靠性，本文提出交叉路口基于車輛權值分簇的中繼轉發方案。仿真結果表明，所提的車輛權值分簇算法可提高鏈路的穩定性，且在Nakagami 衰落信道條件下，采用雙向DF 的中繼轉發方式，數據傳輸的可靠性提高6%。