一種基于狀態轉移的雷達脈沖時序特征描述方法

廖 帥，馬 健，陳茂香，赫 巖，趙永寧

（北京市遙感信息研究所，北京100094）

0 引言

雷達電子目標在對特定空域進行搜索、引導時，一般按照時間序列發射、回收特定的脈沖序列，同時使用各種脈沖重復間隔調制序列來解決模糊和遮蓋等技術問題，實現空域掃描優化等意圖。因此，雷達脈沖序列反映出輻射源的某些特性，隱含著目標的技術狀態、工作模式、活動規律等重要信息，具有時間序列的明顯活動規律。雷達脈沖序列時序分析主要是研究不同序列之間的切換情況，主要包括時序上相鄰的2 種頻繁序列切換時的切換頻度、過渡時間、載頻以及脈寬變化等。

圍繞新體制多功能雷達快速發展技術背景下的電子信號處理，國內外研究人員針對信號建模、特征描述、分析識別等相關問題，開展了大量研究工作。傳統的雷達脈沖序列描述，主要是基于PRI 變換的序列搜索，是根據PRI 變換法，得到脈沖序列中潛在的PRI 值，再根據該值對脈沖序列進行套取，確定該雷達目標。在序列搜索過程中，首先需要確定起始脈沖，將起始脈沖作為跳板向后繼續搜索脈沖，從而實現對整個雷達脈沖時序的搜索和描述。傳統方法主要是基于信號分選對仿真信號進行處理，本文提出了一種基于狀態轉移矩陣的雷達脈沖時序特征描述方法，旨在挖掘出雷達脈沖重復間隔模式，完成局部時序的拼接，描述整個雷達信號的脈沖時序特征，從而為雷達信號時序研究和電子信息處理提供依據。

1 雷達脈沖時序特征

雷達脈沖通常是重復的，但脈沖之間的間隔是可以改變的。即使間隔本身可能并不重復，但一般仍將該間隔說成是雷達使用的脈沖重復間隔。脈沖重復間隔指的是一個雷達脈沖的前沿到下一個雷達脈沖前沿之間的時間間隔。通常的脈沖重復間隔變化類型，如表1 所示。

表1 雷達信號脈沖重復間隔變化類型

電子信號處理中的雷達脈沖時序特征對象是經過分選識別的雷達輻射源脈沖，受限于信號分選系統能力，一般分選出的雷達脈沖不可避免地會存在漏脈沖、脈沖分裂、多源交疊等問題，其真實脈沖到達時間（TOA）序列被嚴重淹沒。傳統的脈沖到達時間差（TDOA）計算采用差分法，即認為分選出全脈沖具有正常的TOA 時序。但是實際上，受接收機性能、信噪比起伏、電磁環境復雜等因素影響，獲取的雷達輻射源脈沖TOA 時序很難準確反映雷達發射脈沖的實際序列，主要表現在三個方面：

1）脈沖分裂。接收機將一個脈沖分成多個脈沖進行檢測，偵獲的輻射源全脈沖多出若干分裂脈沖，在某些連續片段中表現出明顯的時序異常。2）脈沖合并。接收機未檢測到某些中間脈沖，中間脈沖缺失，差分得到的TDOA 為多個脈沖PRI 的和值。3）脈沖缺失。在信號分選時沒有完全選出同一輻射源的脈沖，導致輻射源全脈沖不完整，在某些連續片段中表現出明顯的脈沖缺失現象。

2 基于狀態轉移的雷達脈沖時序特征描述

本文提出的基于狀態轉移矩陣的雷達脈沖時序特征描述方法，將脈沖序列之間的變化關系劃分為2種類型，一種是脈沖序列之間固定切換的形式，一種是脈沖序列之間切換存在一定概率的形式。基于狀態轉移矩陣，實現全部脈沖序列的拼接，從而對整個雷達信號的脈沖時序特征進行描述。

2.1 固定序列切換模型

某些常規體制雷達信號模式有限，時序簡單，其頻繁序列片段一般具有固定的上下級切換關系。固定序列切換模式，主要描述序列之間固定切換的情況。圖1 為雷達脈沖序列切換示意圖，圖中畫出了3個頻繁序列，序列1 具有6 個級聯脈沖，序列2 有3 個級聯脈沖，序列3 有5 個級聯脈沖，黑色點為頻繁序列的起始脈沖，灰色點為終止脈沖，序列之間通過公用脈沖TOA 進行連接，通過識別公用脈沖TOA 對序列切換進行判斷。圖1 中的3 個序列片段切換順序為：序列1―序列2―序列3。

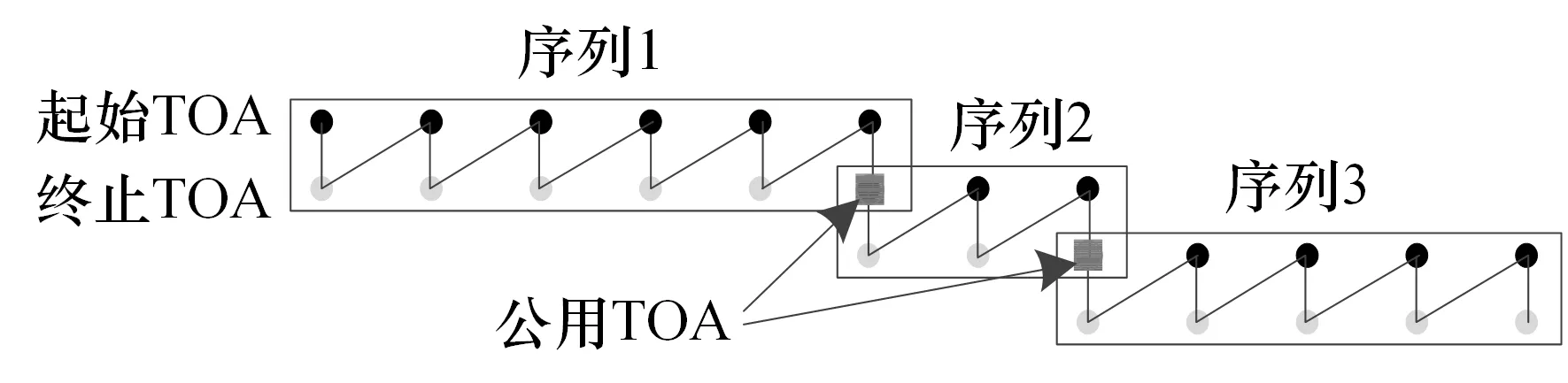
圖1 固定序列切換示意圖

還有一類較為復雜的序列切換情況，某些雷達在模式切換時使用過渡脈沖調整系統狀態，體現在脈沖時序上為頻繁序列之間存在短暫的雜亂脈沖，這些脈沖一般不具有規律性，但是總的時長可能是固定的。圖2 為2 個序列通過2 個過渡脈沖連接。

對于這些具有固定時序的雷達信號，采用切換矩陣的方式對頻繁序列之間的切換時序進行研究。切換矩陣用來統計所有頻繁序列之間的切換頻度，主流切換時序一般具有明顯的聚集性，可見后續仿真結果。

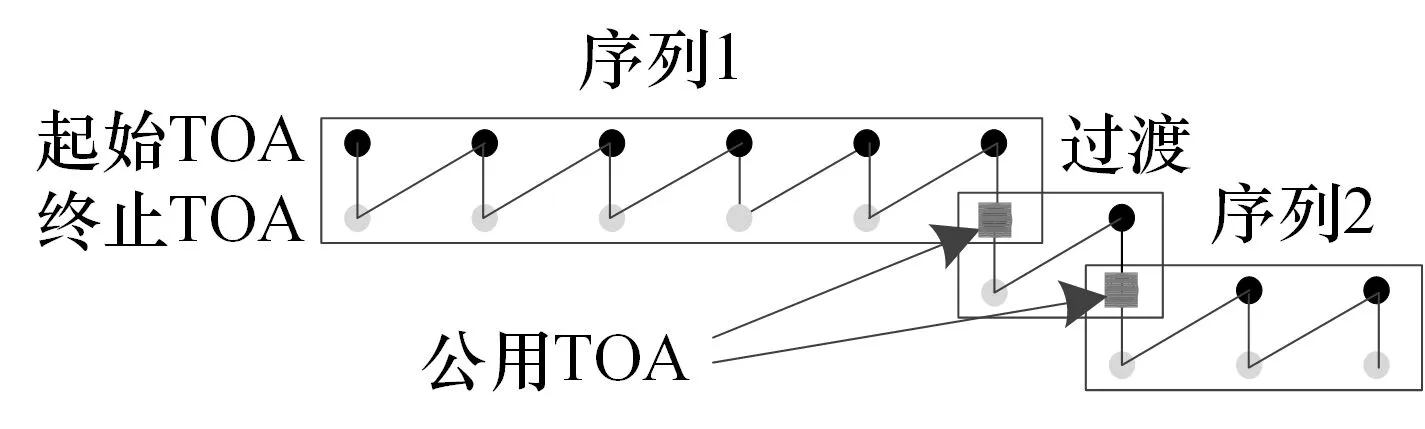
圖2 固定序列切換過渡脈沖示意圖

2.2 狀態轉移概率模型

復雜體制雷達信號模式切換一般不具有固定的切換時序，各個時序片段的切換過程從統計情況來看一般具有多種上下級關系，對這種不具有固定時序的序列切換過程，可以采用隨機過程中狀態轉移概率模型的概念對序列切換時序進行更細化的研究。根據概率論與數理統計知識可知，當試驗次數相當大的時候，頻率可以作為概率的一個近似，或者說概率是可以通過頻率來測量。因此，在應用統計的方法估算概率矩陣時，可以用狀態轉移的頻率近似地估計轉移概率。

這種隨機過程中的狀態轉移模型符合馬爾科夫過程，馬爾科夫鏈即為時間離散、狀態離散的馬爾科夫過程。對于馬爾科夫鏈，描述它的概率性質的最重要的量是一步轉移概率。概率pij(m)為系統在時刻m時處于狀態i 的條件下，下一時刻轉移到狀態j 的一步轉移概率，簡稱轉移概率，為：

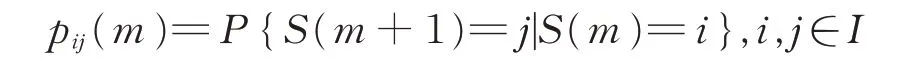
通常可以把上述轉移概率寫成矩陣形式，稱矩陣P(m)為{S(n)}的一步轉移概率矩陣，簡稱轉移矩陣，為：

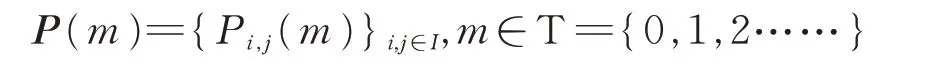
稱矩陣元素pijk(m)為系統在時刻m 時處于狀態i的條件下，經k 步轉移到狀態j 的k 步概率，為：

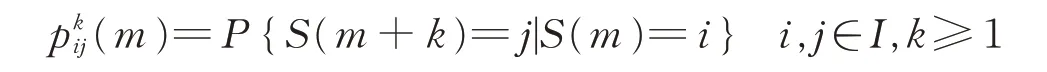
本文采用隨機過程中的狀態轉移模型來描述復雜體制雷達信號模式切換過程，切換過程如圖3 所示。

具有6 個級聯脈沖的序列1，按照工作狀態可以切換至具有3 個級聯脈沖的序列2，也可以切換至具有6個級聯脈沖的序列3。經過統計，從序列1 切換至序列2 和序列3 滿足一定的概率值，序列1 切換至序列2 的概率為a/N，切換至序列3 的概率為1-a/N。

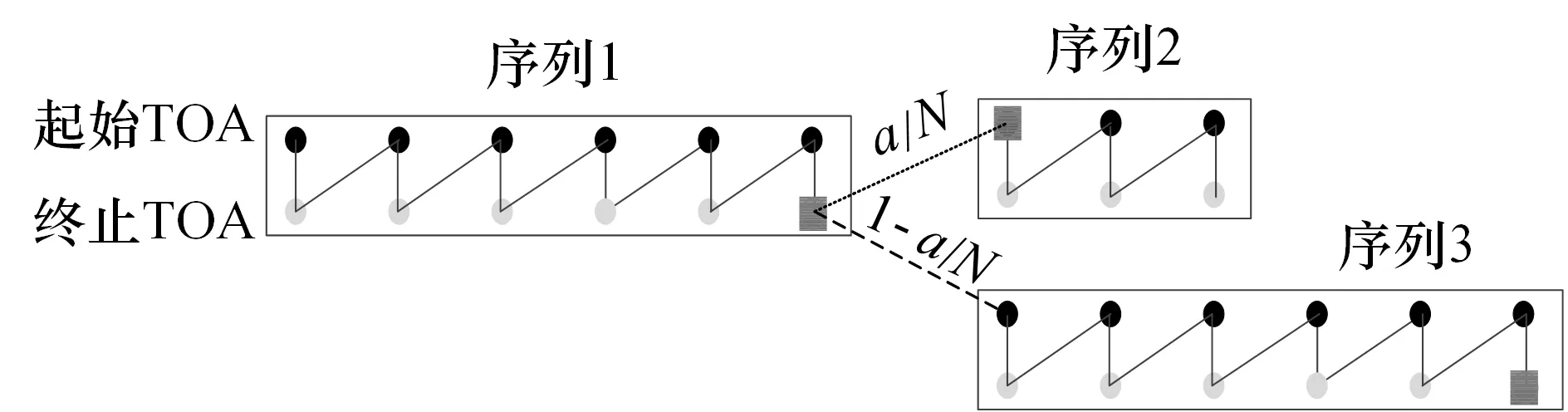
圖3 狀態轉移序列切換示意圖

3 仿真試驗

3.1 固定序列切換模型仿真

仿真脈沖重復間隔組變的雷達信號，組變序列按照固定的時序進行循環排列，共仿真70 s 的信號，產生167 952 個脈沖，在脈沖時序中隨機加入干擾脈沖信號，仿真信號時序完整度為85%。采用序列提取技術對仿真的167 952 個脈沖的頻繁序列進行提取，結果如表2 所示（表中N1、N2、N3、N4、N5、N6為整數），該結果與仿真的組變序列完全一致。

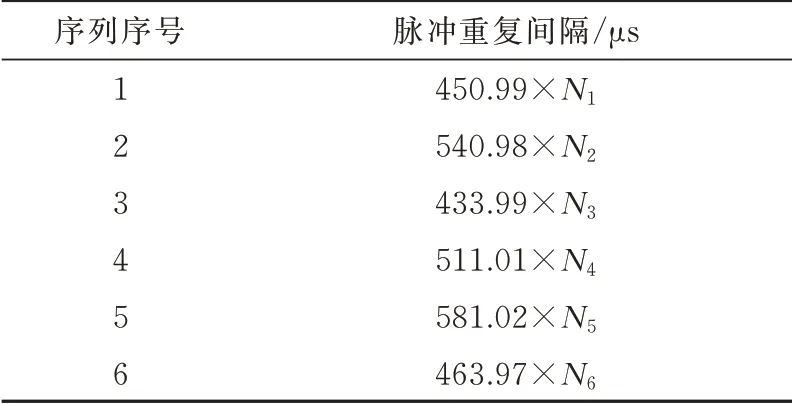
表2 仿真脈沖重復間隔組變雷達序列片段

對上述仿真信號得到的雷達序列片段，提取序列切換時序，構建的切換矩陣如表3 所示。表中數字表示，統計過程中，從縱向序列轉移到橫向序列的次數。如：3 394 為表示從序列1 切換到序列6 的次數。由于脈沖時序中存在干擾，序列之間的切換會存在誤差，可以設定次數閾值大于500 時為有效次數。

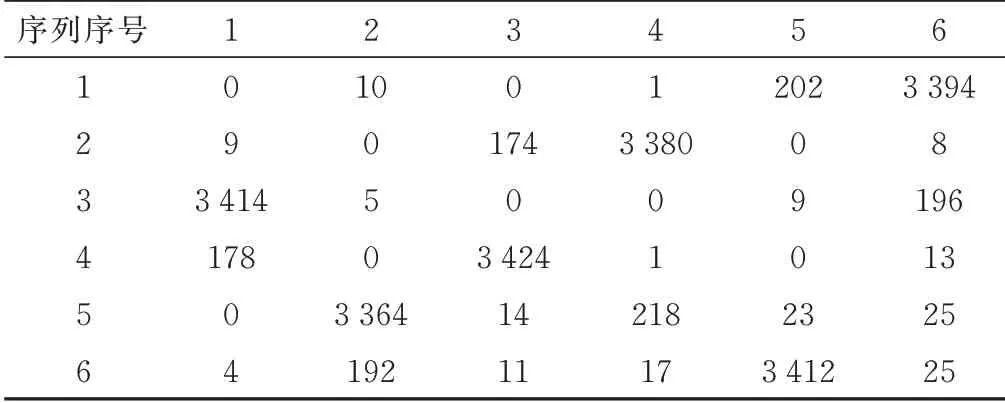
表3 仿真脈沖重復間隔組變雷達序列切換矩陣

通過序列切換矩陣，得到主流切換時序如下，該固定時序提取結果與仿真信號樣式一致:1→6→5→2→4→3→1。

3.2 狀態轉移概率模型仿真

利用相同方式仿真復雜體制雷達信號脈沖，采用序列提取技術對仿真脈沖信號頻繁序列進行提取，結果如表4 所示（表中M1、M2、M3為整數），該結果與仿真的組變序列完全一致。

通過對仿真的復雜體制雷達信號脈沖進一步進行聚類分析，可以得到各序列之間的切換關系，如表5所示。從表中可以看出該仿真雷達信號的序列2、序列4 及序列5 相互之間存在主要的切換關系，且序列2、序列5 自身也存在主要的切換關系。

表5 各單元格中每一列依次對應聚類DTOA 和聚類脈沖數，設置切換頻度門限為10。其中，序列2 切換到序列2 有2 種情況，（641+376）μs（約為1 018 μs）的情況出現81 次，0 μs（約為2 μs）的情況出現37 次；序列2 切換到序列4 只有一種情況，（641+383）μs（約為1 024 μs）的情況出現73 次。序列4 切換到序列5 只有一種情況，0 μs（約為1 μs）的情況出現32 次。序列5切換到序列2 只有一種情況，（383+222+376）μs（約為978 μs）出 現97 次；序 列5 切 換 到 序 列5 有 三 種 情況，（383+222+383）μs（約為986 μs、994 μs、980 μs）的情況出現243 次（190+42+11），（383+383）μs 的情況出現11 次，0 μs 的情況出現25 次。結合序列切換時脈沖序列特點，對聚類DTOA 進行分解后可以得到狀態轉移概率矩陣如表6 所示，狀態轉移概率模型即為研究序列切換到不同的后級序列的具體情況。

以鏈式圖的形式描述上述狀態轉移概率模型如圖4 所示，該模型具有2、4、5 三個狀態，鏈式圖標注了狀態之間的過渡脈沖以及各種狀態切換頻率。

表4 仿真復雜體制雷達序列片段

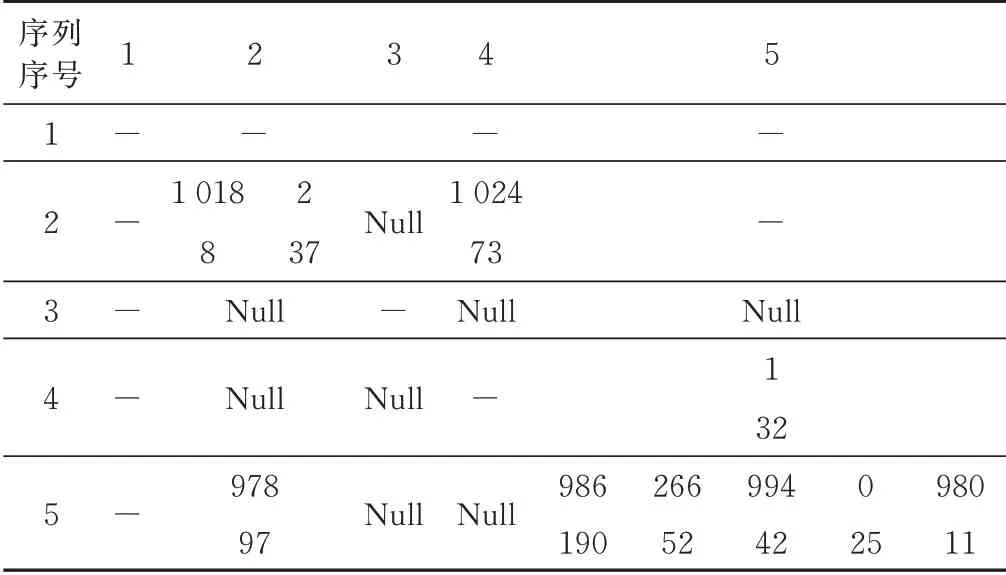
表5 仿真復雜體制雷達序列切換DTOA（μs）聚類結果

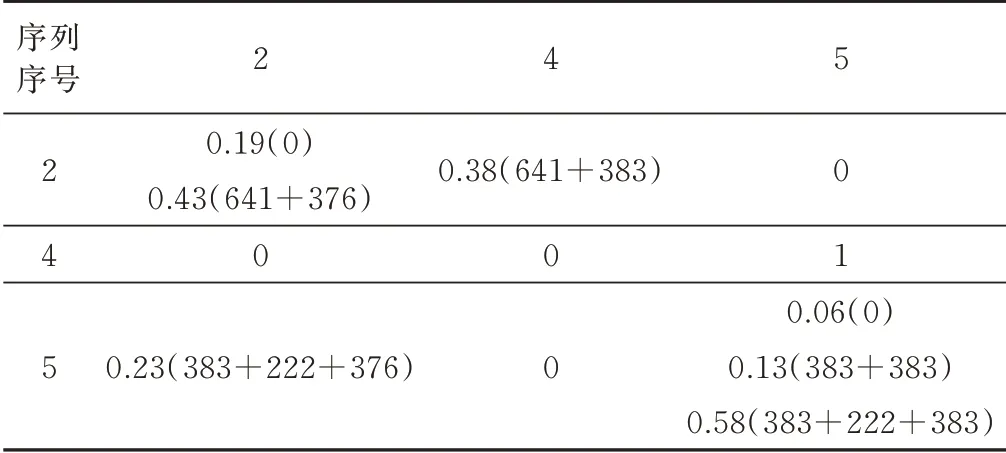
表6 仿真復雜體制雷達序列切換的狀態轉移概率矩陣

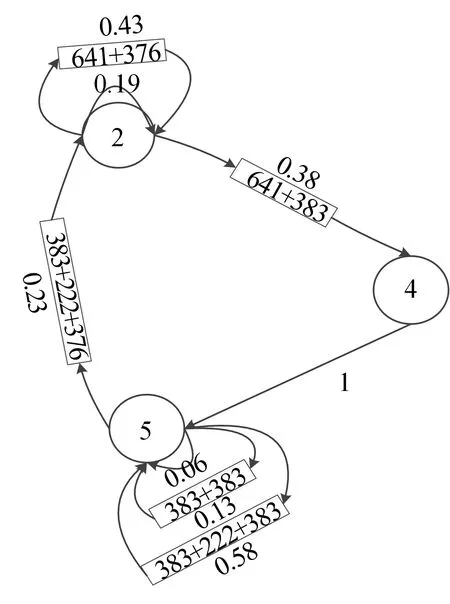
圖4 復雜體制雷達序列切換的狀態轉移鏈式圖

4 結束語

本文提出的一種基于狀態轉移矩陣的雷達脈沖時序特征描述方法，相比傳統的基于脈沖描述字提取雷達信號脈沖序列片段的方法，旨在挖掘出雷達脈沖重復間隔模式，完成局部時序的拼接，描述整個雷達信號的脈沖時序特征，從而為雷達信號時序研究和電子信息處理提供依據。仿真實驗表明，該方法在描述固定序列和復雜體制雷達信號脈沖序列均存在明顯優勢。■