大過載真空傳感器失效分析

李玉欣，陳寶成，孫 帥，姜曉龍

(1.中國航天員科研訓練中心，北京 100094；2.中國電子科技集團公司 第四十九研究所，哈爾濱 150001)

0 引言

應用物理與技術中的真空是指低于一個大氣壓的稀薄氣體的空間狀態，其應用領域十分廣泛，已經滲透至車輛工程、土木建筑、機械、包裝、環境保護、醫療器械、石油、化工、食品、半導體、電子、航空航天等領域。而真空傳感器是用于測量低于一個大氣壓氣體的儀器。其中電容式真空傳感器相比于熱傳導型電阻式、皮拉尼、熱傳導型熱偶等類型真空傳感器具有精度高、線性好、量程寬、與被測介質成分無關、重復性好等優點，逐漸成為真空測量領域內的研究熱點之一[1-4]。

某型號真空傳感器采用電容式原理，用于實時監測氣體管路中的氣體壓力，即管路真空度。但對已交付使用的電容式真空傳感器進行跟蹤，均很快發生失效，傳感器產品輸出異常。將失效的傳感器產品進行復測，產品輸出在不同壓力情況下均不發生變化，接近滿量程輸出不變。根據傳感器的組成及特點，可能造成產品失效的原因有兩個：(1)調理電路或濾波電路中的某一器件失效，造成傳感器產品輸出異常；(2)傳感器結構發生變化，導致輸出異常。為提升該真空傳感器的可靠性，滿足其在實際工程中的使用需求，需進一步對產品的失效進行分析，確定失效機理。

1 電容式真空傳感器工作原理及組成

1.1 電容式真空傳感器工作原理

電容式傳感器的工作原理基于平板電容原理，為變極板間距型，此類型傳感器結構原理如圖1所示[5-8]。

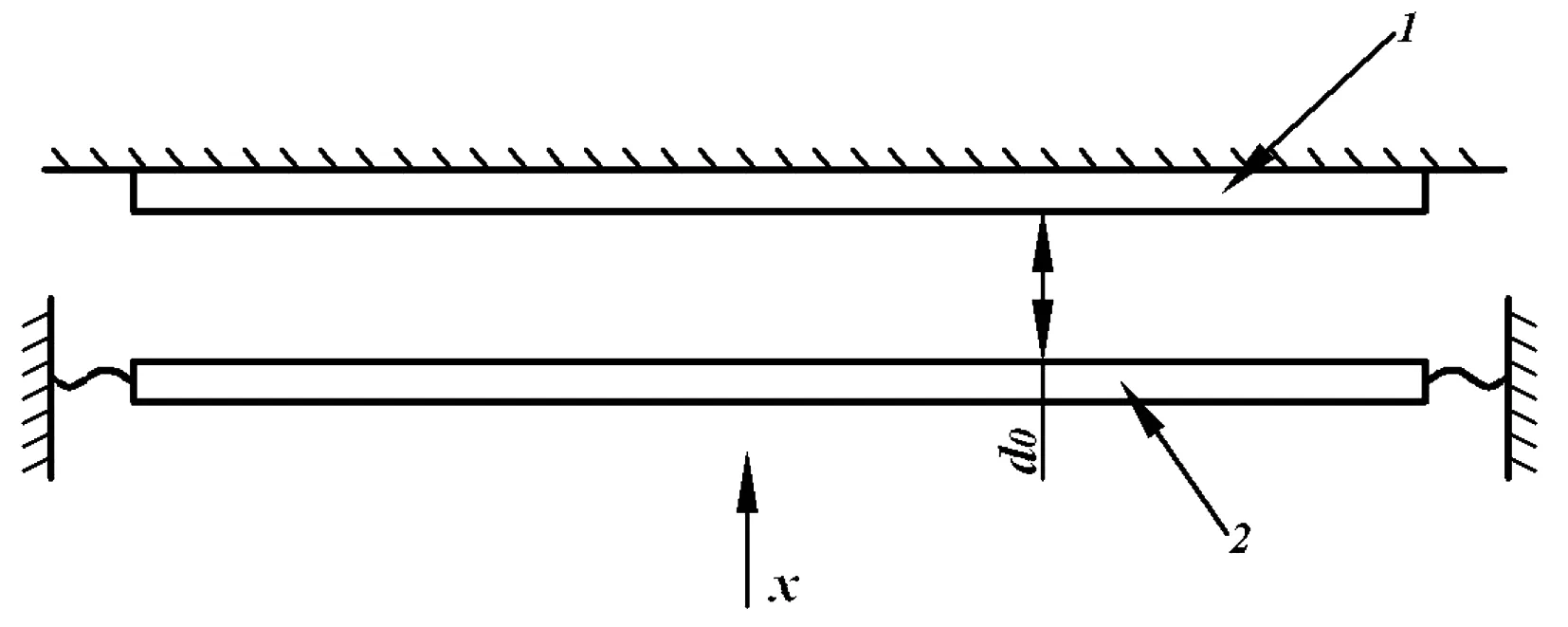
圖1 變間距型電容傳感器工作原理Fig.1 Working principle of changing spacing electric capacity sensor

圖1中極板1固定不動，兩極板間距d0變化，使電容量產生變化。C隨d變化的函數關系為一雙曲線，如圖2所示。

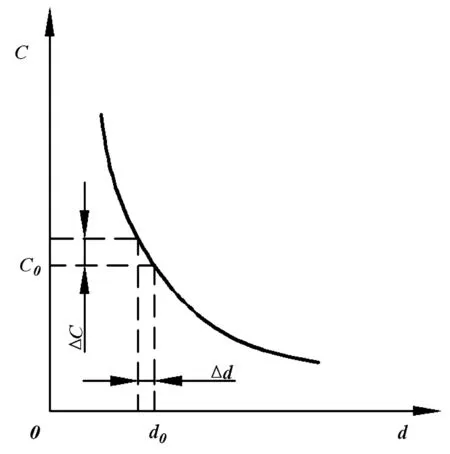
圖2 C-d特性曲線Fig.2 C-d characteristic curve

設動片2位移未發生變化，即極板初始間距為d0，且初始電容量為C0，則：

C0=S/3.6πd0

(1)

當極板間距d0減小Δd時，電容量為：

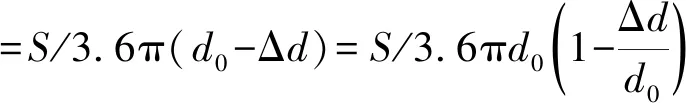
(2)

則：

(3)

當Δd?d0時，公式(3)可以展開為級數形式，即：

(4)

忽略公式(4)中的高次項，得到：

(5)

由公式(5)可知，在Δd/d0?1的條件下，電容的變化量ΔC與極板間距變化量Δd近似為線性關系。可以理解為電容的變化與真空壓力呈正比，與兩個極板之間的距離成反比[9-10]。

1.2 電容式真空傳感器組成

電容式真空傳感器由真空計、電路組件、結構部分(包括絕緣支架、絕緣墊圈、連接法蘭、O型圈、外殼、上蓋以及支撐和固定電路組件的其它結構件等)以及電氣連接部件組成，具體見圖3所示。

圖3 電容式真空傳感器構成圖Fig.3 Capacitive vacuum sensor composition diagram

其中，電容式真空計是該傳感器的核心工作部件，其由進氣管、膜片基座、金屬膜片、固定電極、上蓋和引出電極等組成，如圖4所示。

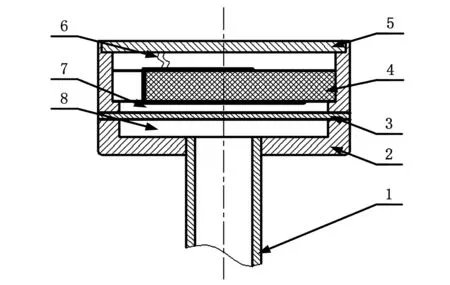
1-進氣管 2-膜片基座 3-金屬膜片 4-固定電極 5-上蓋 6-引出電極 7-真空腔 8-檢測腔圖4 電容式薄膜真空計組成Fig.4 Electric capacity type thin film suction gauge composition

2 電容式真空傳感器失效分析

2.1 電路組件分析

電容式真空傳感器電路組件中主要包括運算放大器、頻壓轉換器、穩壓器、電阻、電容，等等，其電路組件如圖5所示。

圖5 電容式真空傳感器電路組件Fig.5 Capacitive vacuum sensor circuit components

根據電容式真空傳感器的電路原理圖，分別測量電路組件中的各個電子元器件電性能指標并進行排查，未發現輸出異常情況。排除電路組件導致傳感器輸出異常，發生失效情況。

2.2 結構部分分析

將已經失效的電容式真空傳感器產品進行解剖，觀察結構件狀態。其中，固定電極因已與殼體固結且厚度較厚(6.5 mm)，未發生任何變化。而動電極因與固定電極的間隙小(0.1 mm)且其厚度薄(0.04 mm)，當其發生形變，也無法進行實際觀察。根據電容式真空傳感器的故障樹及其結構組成，真空計中的動電極為傳感器中較為薄弱環節，進而根據傳感器產品使用的金屬材料，搜集其在實際工程中的環境應力、工作應力，建立產品動電極的有限元模型，需進一步對其分析。

2.2.1 有限元模型建立

電容式真空傳感器兩電極之間的初始距離很小，為0.1 mm，動電極采用鎳基合金，為金屬薄膜，采用有限元的分析方法對其進一步考察。

傳感器定電極在其工作過程中相對靜止，在有限元分析時施加固定約束。為驗證有限元模型建立的正確性，在動電極上施加100 Pa滿量程的壓強，分析其動力學狀態。

由圖6可知，位移發生在動電極圓心處(分析采用1/2某一截面，該模型屬于中心對稱模型)，最大位移量為0.062 476 mm，小于兩電極間的0.1 mm距離。

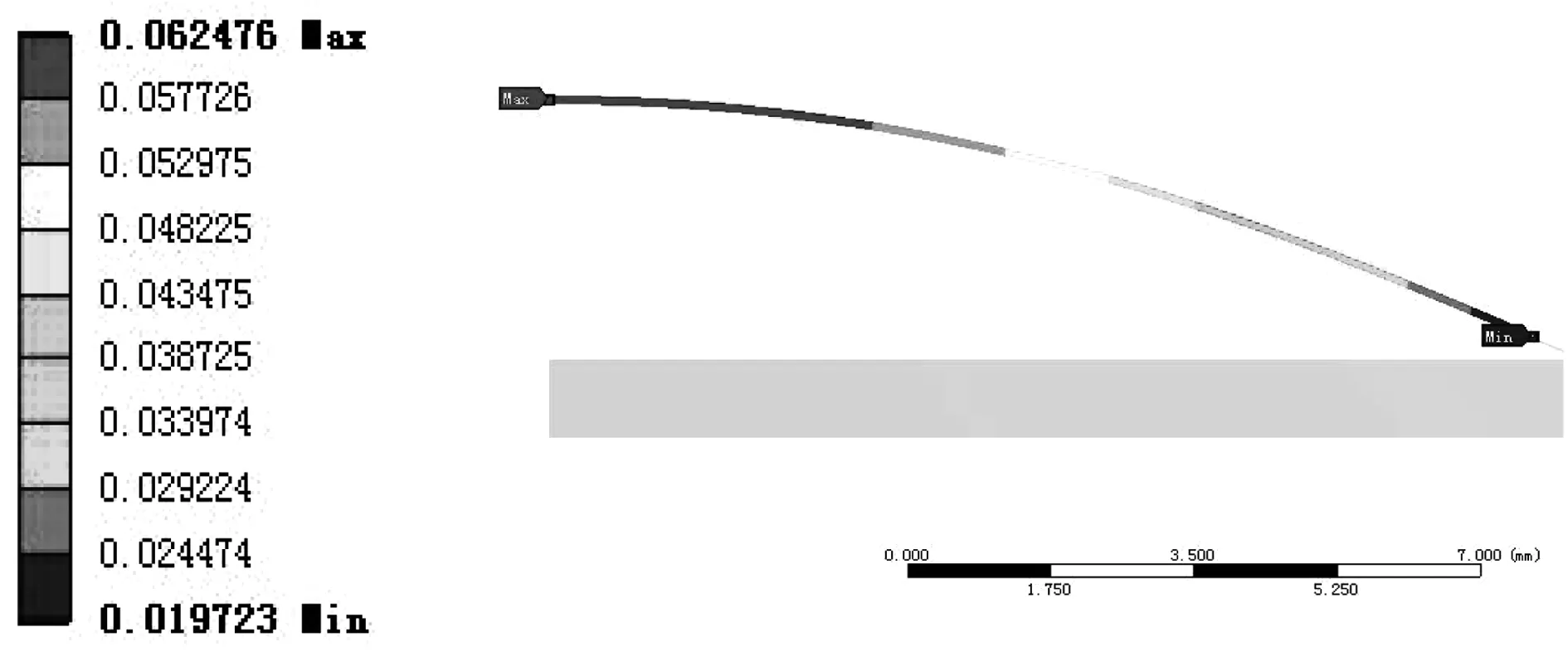
圖6 動電極在100Pa下的位移云圖Fig.6 Dynamic electrode under 100Pa displacement cloud chart

圖7為動電極在100 Pa壓強下的應力云圖。由圖7可知，最大應力發生在動電極的根部與殼體固結處，最大應力為13.76 MPa，遠小于鎳基合金的疲勞極限強度和抗拉強度，因此傳感器在正常工作載荷條件下，能夠正常、穩定、可靠地工作。

圖7 動電極在100 Pa下的應力云圖Fig.7 Dynamic electrode under 100 Pa stress cloud chart

2.2.2 有限元模型驗證

為驗證有限元模型建立的準確性，應用彈性力學中變分法解決電容式真空傳感器動電極的薄板大撓度、軸對稱及承受均布載荷問題。

采用MATLAB R2014a進行計算，以下為應用該計算方法所編程的程序：

E=213.7e+9;

u=0.29;

t=0.04e-3;

q0=100;

a=16.5e-3;

D=(E*t^3)/(12*(1-u^2));

syms C0;

C0=solve(C0+0.486*C0^3/(t^2)==q0*(a^4)/(64*D),C0);

P=[0.486/(t^2) 0 1 -q0*(a^4)/(64*D)];

C=roots(P);

C0=C(3,1);

r=(-a:0.0001:a);

w=C0.*(1-r.^2./a.^2).^2;

plot(r*1000,w*1000)

根據以上程序，在傳感器受到滿量程100 Pa時，動電極中心位置的最大撓度如圖8所示。

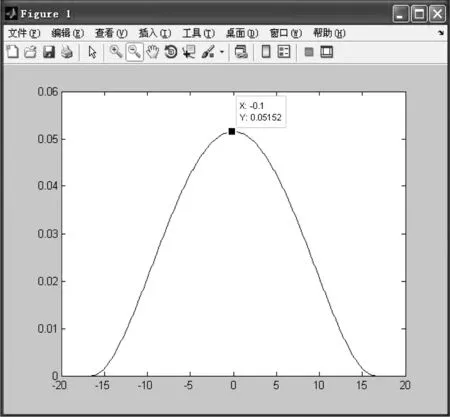
圖8 動電極撓度計算結果Fig.8 Dynamic electrode deflection computed result

由圖8可知，通過理論計算結果，傳感器動電極最大撓度為0.051 52 mm。分析出現偏差的原因為：在軟件仿真分析時，添加的邊界條件存在一定誤差，單元格的數量有限，不能精確反映彈性體的特性，因此造成二者的計算結果存在一定偏差。該理論計算結果可以證明建立的有限元模型可準確分析傳感器所處的動力學狀態，且傳感器有限元分析結果也可準確反映傳感器的失效模式。

2.3 電容式真空傳感器失效分析

2.3.1 二倍過載

與電容式真空傳感器滿量程工作時施加的邊界條件一致，對定電極施加固定約束，在動電極的圓周上施加固定約束。在動電極上施加200 Pa壓強，分析其動力學狀態。

圖9為動電極在200 Pa壓強下的位移云圖。由圖9可知，位移發生在動電極的圓心處(分析采用1/2某一截面，該模型屬于中心對稱模型)，最大位移量為0.071 952 mm，小于兩電極之間的0.1 mm距離。

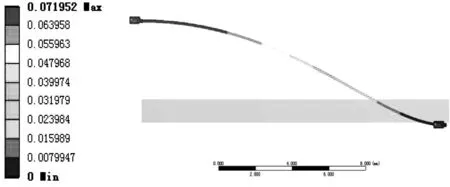
圖9 動電極在200Pa下的位移云圖Fig.9 Dynamic electrode under 200 Pa displacement cloud chart

圖10為動電極在200 Pa壓強下的應力云圖。由圖10可知，最大應力發生在動電極的根部與殼體固結處，最大應力為15.772 MPa，遠小于鎳基合金的疲勞極限強度和抗拉強度。

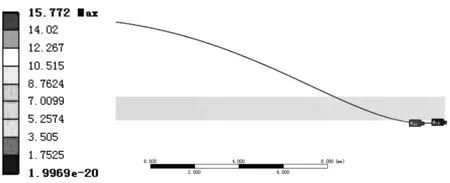
圖10 動電極在200 Pa下的應力云圖Fig.10 Dynamic electrode under 200 Pa stress cloud chart

2.3.2 四倍過載

與電容式真空傳感器滿量程工作時施加的邊界條件一致，對定電極施加固定約束，在動電極的圓周上施加固定約束。在動電極上施加400 Pa壓強，分析其動力學狀態。

圖11為動電極在400 Pa壓強下的位移云圖。由圖11可知，位移發生在動電極的圓心處(分析采用1/2某一截面，該模型屬于中心對稱模型)，最大位移量為0.1 mm，此時動電極的最大位移已與電容板兩電極之間的距離相等，即動電極的圓心與陶瓷固定電極貼合，形成了閉合回路，傳感器是否能夠正常工作，還需要考察動電極的受力情況。

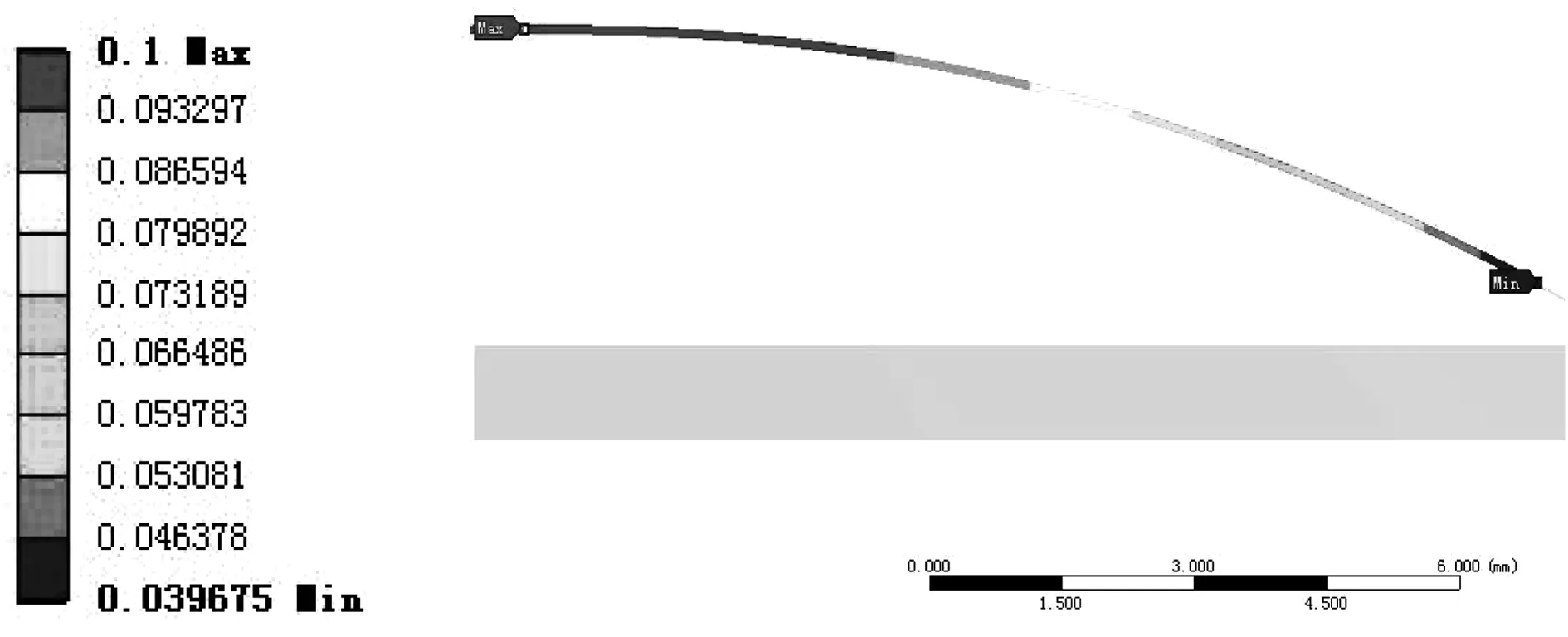
圖11 動電極在400 Pa下的位移云圖Fig.11 Dynamic electrode under 400 Pa displacement cloud chart

圖12為動電極在400 Pa壓強下的應力云圖。由圖12可知，最大應力發生在動電極的根部與殼體固結處，最大應力為37.27 MPa，遠小于鎳基合金的疲勞極限強度和抗拉強度，傳感器仍能夠正常工作。

圖12 動電極在400 Pa下的應力云圖Fig.12 Dynamic electrode under 400 Pa stress cloud chart

2.3.3 千倍過載

與電容式真空傳感器滿量程工作時施加的邊界條件一致，對定電極施加固定約束，在動電極的圓周上施加固定約束。在動電極上施加100 kPa壓強，分析其動力學狀態。

圖13為動電極在100 kPa壓強下的位移云圖。由圖13可知，位移發生在動電極的圓心處(分析采用1/2某一截面，該模型屬于中心對稱模型)，最大位移量為0.100 02 mm，此時動電極的最大位移已與電容板兩電極之間的距離相等，即動電極的圓心與陶瓷固定電極貼合，形成了閉合回路，傳感器是否能夠正常工作，還需要考察動電極的受力情況。

圖13 動電極在100 kPa下的位移云圖Fig.13 Dynamic electrode under 100kPa displacement cloud chart

圖14為動電極在100 kPa壓強下的應力云圖。由圖14可知，最大應力發生在動電極的根部與殼體固結處，最大應力為319.64 MPa，已經達到鎳基合金320 MPa的疲勞強度極限。在該載荷作用下，動電極會很快發生低周疲勞及塑性變形，導致傳感器的失效。

圖14 動電極在100 kPa下的應力云圖Fig.14 Dynamic electrode under 100 kPa stress cloud chart

3 電鏡掃描分析

為驗證仿真分析結果及計算結果的正確性，將發生失效的電容式真空傳感器斷裂的動電極取樣，重點截取應力較大的根部進行觀察。圖15為動電極斷面的放大圖，從圖中可以觀察到存在“縮頸”現象，即材料發生了塑性變形。

圖15 動電極斷面電鏡掃描圖Fig.15 Brake pads section electric mirror scans

進一步將圖15中圈出的部分再一次進行放大，如圖16所示。圖16存在明顯的“拉伸縮頸”現象，動電極的金屬材料發生了塑性變形。在千倍過載的情況下，動電極根部的應力趨近屈服極限，造成鎳基合金材料的塑性變形，導致電容極板即使受到介質壓力的情況下也不會發生變形，極板間距不發生變化，導致電容式真空傳感器的輸出不發生變化。

圖16 動電極斷面局部放大圖Fig.16 Brake pads section local enlargement chart

4 結論

某工程型號中交付使用的電容式真空傳感器在實際使用過程中發生輸出異常現象。通過對失效產品的解剖和分析，電路部分未有異常現象，排除電子元器件故障導致產品失效的情況。進一步對失效傳感器產品的結構進行分析，建立電容式真空傳感器的有限元模型，考察在100 Pa滿量程情況下的動電極的位移。同時，采用變分法，應用MATLAB軟件進行傳感器產品在滿量程100 Pa下動電極撓度的理論計算，驗證了有限元模型建立的準確性。

以驗證后的有限元模型為分析對象，分別考察電容式真空傳感器在滿量程、二倍過載、四倍過載及千倍過載的應力、應變和位移情況。由分析結果可知，傳感器產品動電極在四倍過載的壓力下，其位移已經達到與固定電極之間的初始距離，但動電極仍為彈性變形范圍內。動電極在千倍過載壓力的情況下，發生塑性變形，在壓力消失后，不能恢復至初始狀態，出現在不同壓力情況下輸出基本保持滿量程輸出的失效現象。

為驗證有限元分析的正確性，應用電鏡對失效傳感器的動電極截面進行觀察，存在明顯的“縮頸”現象，證明了分析的正確性。