鐵路新型整體剛性面板加筋土擋墻現場試驗研究
牛笑笛,楊廣慶,周詩廣,楊國濤,王智猛,王 賀
(1.石家莊鐵道大學 省部共建交通工程結構力學行為與系統安全國家重點實驗室,河北 石家莊 050043;2.石家莊鐵道大學 交通運輸學院,河北 石家莊 050043;3.石家莊鐵道大學 土木工程學院,河北 石家莊 050043;4.中國鐵道學會,北京 100844;5.中國國家鐵路集團有限公司,北京 100844;6.中鐵二院工程集團有限責任公司,四川 成都 610031)
近年來,隨著我國鐵路、公路和機場等交通基礎設施的大規模建設,加筋土擋墻以其穩定性好、造價低、占地少和施工便捷的特點得到了廣泛的應用[1-2]。我國過去建造的加筋土擋墻以模塊式、返包式為主,較少應用整體剛性面板加筋土擋墻。
整體剛性面板加筋土擋墻的設計理念最早由Tatsuoka 教授提出,相應施工技術體系稱為RRR工法。此類擋墻通過采用較大剛度的整體墻面板,可增加擋墻整體穩定性[3]。針對整體剛性面板加筋土擋墻的研究,國內外學者已取得了一定的成果。Tatsuoka 等[4-5]從施工方法、設計原理、抗洪能力等方面進行了綜合研究,并對其進行了推廣應用。Kongkitkul等[6]研究了在全尺度擋墻中土工格柵拉力隨時間的變化。Kuwano等[7]分析了地震中擋墻的抗震性能。Uchimura 等[8]進行了預應力作用下擋墻的加載試驗,研究了擋墻在橫向荷載、縱向荷載作用下的位移變化。徐鵬等[9-10]開展了相應振動臺模型試驗,得到了地震力作用下的位移、加速度、土壓力、筋材拉力的變化規律,并利用雙砌塊法推導了屈服加速度系數關系式,分析了筋材抗拉強度、筋材布置方式等對屈服加速度的影響。葉觀寶等[11]利用Plaxis 對整體剛性面板加筋土擋墻和其他形式加筋土擋墻進行有限元分析,研究面板形式對擋墻力學性能的影響。廖紅建等[12]通過模型試驗研究了配筋率、鋪筋層數等對此類擋墻整體穩定性的影響。陳建峰等[13-14]進行了相同軟土地基條件下此類加筋土擋墻和單一柔性墻面加筋土擋墻的離心模型試驗,比較分析了2 種擋墻在墻頂均布荷載作用下的工作性狀;并基于離心模型試驗,采用離散元軟件PFC 和有限差分軟件FLAC3D分別模擬加筋土擋墻和軟土地基,分析其內部、外部穩定性。針對整體剛性面板加筋土擋墻的現有研究多側重于室內試驗與數值模擬,現場試驗數據相對較少,對此類擋墻的后續建設指導意義有限。
成昆鐵路復線加筋土擋墻為我國在RRR 工法基礎上進行改進后建造的鐵路新型整體剛性面板加筋土擋墻。本文以此擋墻為工程依托,通過現場原位試驗,研究其施工期及工后的基底應力、返包體背部土壓力、格柵應變、墻體壓縮量和墻面位移的變化規律。
1 工程概況
試驗段位于成昆鐵路復線(國鐵Ⅰ級)DK443+764.81—DK443+894.55 段,基底2 m 換填圓礫石,左右兩側均應用新型整體剛性面板加筋土擋墻,擋墻高度為6.6 m,共鋪設22層格柵。具體施工如下。
(1)首先使用C35 混凝土澆筑面板條形基礎,之后進行加筋體填筑,待加筋體發生一定變形并相對穩定后,使用C35混凝土澆筑面板,面板澆筑前后如圖1所示。澆筑的混凝土砂漿凝固后使面板和返包體連接成為一個整體。通過分階段施工,減小由于面板和加筋體之間的不均勻沉降而造成的墻面局部破壞[15]。

圖1 整體剛性面板加筋土擋墻
(2)格柵豎向間距0.3 m,每1.2 m 進行1 次通鋪,使兩側擋墻形成對拉的穩定結構。非通鋪格柵長度相等,格柵總長度為10 m,其中每層平鋪部分長度為6 m,包裹礫石袋部分長度為1 m,返包回折部分長度為3 m。格柵返包后,用連接棒將返包回折部分與本層平鋪部分進行連接,并拉緊、固定。此種連接方式可有效減小填筑期返包體背部因碾壓而產生的側向位移。
(3)在加筋體內預埋直徑25 mm 的HPB300鍍鋅鋼筋,鋼筋水平間距0.6 m,豎直間距0.6 m。埋入加筋體中的錨固長度為3 m,鋼筋末端焊接水平向的鍍鋅L 型鋼(50 mm×50 mm×5 mm),鋼筋前端伸出加筋體外,與整體現澆面板的鋼筋網連接在一起,起到連接面板與加筋體的作用。
(4)墻面坡率為1∶0.05。面板厚度為0.3 m,內置雙層鋼筋網,與加筋體采用鍍鋅鋼筋連接。面板施工前,返包礫石袋作為臨時面板;面板完成后,礫石袋起到排水和緩沖的作用,并保護面板與鋼筋之間的連接。
加筋土擋墻主體施工歷時曲線如圖2所示,其中加筋體填筑歷時103 d,填筑完成后靜置55 d,面板澆筑歷時35 d。
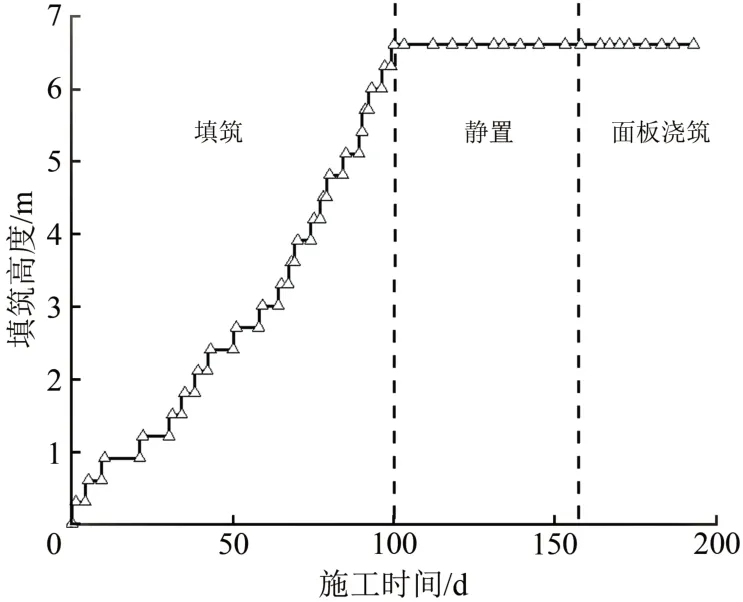
圖2 施工歷時曲線
各項工程指標要求如下。
(1)加筋體分層填筑并碾壓密實,臨近面板1.5 m 范圍內使用輕型壓實機,1.5 m 范圍外使用大型振動壓路機碾壓,壓實度≥92%。填料采用圓礫石,其黏聚力為5 kPa,內摩擦角為38.5°,最優含水率為7.5%,最大干密度為2.31 g·cm-3。
(2)礫石袋采用透水土工袋裝填圓礫石,圓礫石級配良好,滲透系數不小于10-3cm·s-1。
(3)土工格柵采用高密度聚乙烯(HDPE)單向拉伸塑料土工格柵,橫肋間距為30 cm,縱向抗拉強度為120 kN·m-1,峰值應變為11.5%。
面板完成后共發生2 次地震,第1 次發生在面板完成后20 d(2018年10月31日),震級為5.1級,震源(北緯27.7°,東經102.08°)深度19 km,距離現場約10 km;第2 次發生在面板完成后40 d(2018年11月20日),震級為3.3 級,震源(北緯27.69°,東經102.07°)深度14 km,距離現場約12 km。
2 現場試驗測試
對DK443+860 左側斷面進行監測,在第2,6,10,14,17和20層埋設測試傳感器。由于墻體的側向土壓力主要由返包體承擔,在返包體背部水平和豎直方向安裝鋼弦式土壓力盒,測試垂直土壓力和側向土壓力。由于第1層格柵與基礎相接,表面不平順,所以在第2 層水平方向埋設土壓力盒,測試基底垂直應力。在格柵上安裝柔性位移計,測試格柵變形。在墻面處安裝測斜探頭,測試墻面位移。在墻頂和基底分別埋設沉降計,測試路中及路肩沉降。傳感器布置具體位置如圖3所示。
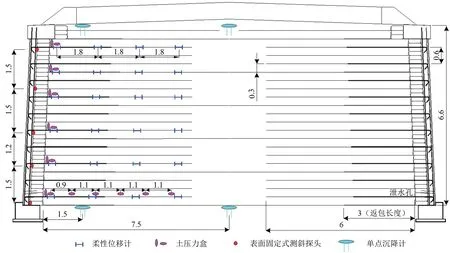
圖3 斷面及儀器布置(單位:m)
3 加筋土擋墻力學分析
為分析擋墻的內部受力狀態及其變形原因,按照每層格柵層數的不同將加筋土擋墻返包體后墻體部分簡化為3 個區域,分別為加筋區1(ABFE)、加筋區2(BCGF)、加筋區3(CDHG),如圖4所示。圖中:加筋區1為墻體內具有返包回折格柵的部分,每層有2 層格柵,寬度為3 m,靠近返包體處使用輕型機械夯實;加筋區2 為加筋區1 后格柵非通鋪的部分,寬度為3 m;加筋區3 為墻體只有通鋪格柵的部分,寬度為3 m,加筋區2 和加筋區3 均使用重型振動壓路機壓實;S1代表非通鋪的格柵;S2代表通鋪的格柵;S3代表返包回折的格柵。
將加筋區1、加筋區2 和加筋區3 單獨進行受力分析,各區域受力如圖5所示。圖中:h1i為各層非通鋪格柵的高度;h2i為各層通鋪格柵的高度;h3i為各層返包回折格柵的高度;i表示由下到上的格柵層數。
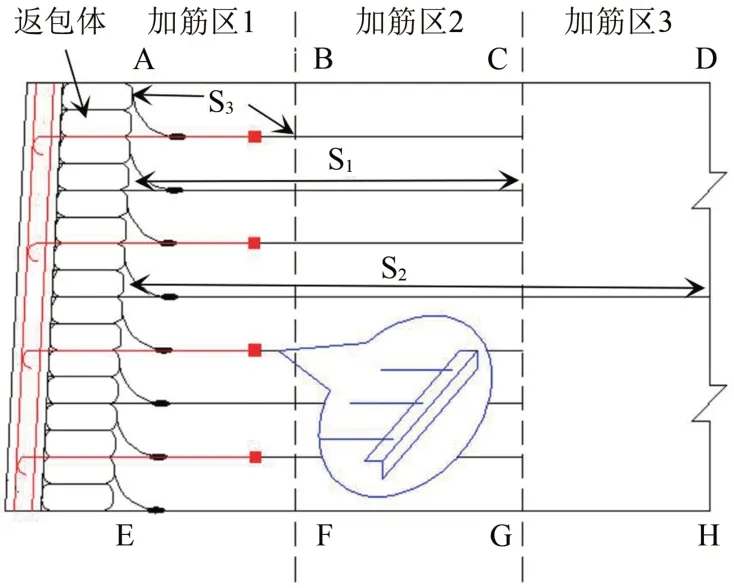
圖4 加筋土擋墻分區模型圖
各加筋區分別承受土體自重Wj(j=1,2,3),基底對擋墻的支撐力Zj(j=1,2,3),格柵網兜效應產生的合力Fj(j=1,2,3)及格柵產生的截面拉力TAEi,TBFi,TCGi和TDHi。此外,返包格柵對加筋區1 產生拉力Ti(沿筋長方向與返包體呈θ角)。假設墻體內等高處由于土體自重引起的側向土壓力值近似相等,計算受力時可相互抵消,此處不計土體自重引起的側向土壓力。
當發生墻體壓縮時,由于格柵層數為加筋區1>加筋區2>加筋區3,受網兜效應的影響,墻體壓縮量為△hAB<△hBC<△hCD。對于3 個區域有以下幾種情形。
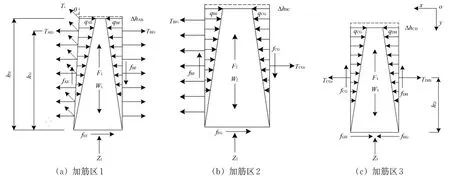
圖5 各區域受力分布
(1)加筋區3 沿其中心線呈對稱分布,土體沿中心向加筋區2 擠壓,基底產生反向的摩擦力fGH和fHG;加筋區2 對其產生向上的摩擦力fCG和fDH及擠壓力。由于由上到下擠壓變形逐漸減小,將擠壓力近似看做線性分布荷載,以qCG和qDH表示。
(2)加筋區2 受加筋區3 擠壓產生向右的基底摩擦力fFG;由于墻體壓縮,兩側產生摩擦力fCG和fBF;由于兩側區域的擠壓產生線性分布的擠壓力qBF和qCG。
(3)加筋區1 受加筋區2 擠壓產生向右的基底摩擦力fEF,由加筋區2和返包體產生的側向摩擦力fAE和fBF及線性分布的擠壓力qAE和qBF。
4 測試結果及分析
4.1 基底垂直應力
圖6給出了填筑期加筋區1 和加筋區2 基底垂直應力沿格柵鋪設方向的分布曲線。
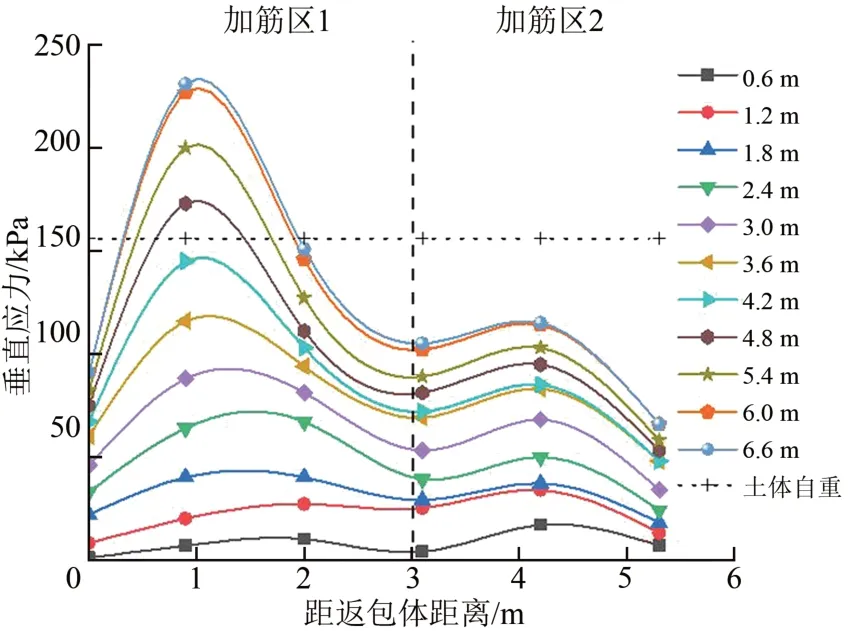
圖6 不同填筑高度下基底垂直應力沿格柵鋪設方向的分布曲線
由圖6可知:隨填筑高度的增加,土體自重W1和W2增加,導致基底垂直應力逐漸增大;基底應力沿筋長方向呈非線性分布,在加筋區1中部和加筋區2 中部分別出現峰值;每層填筑壓實之后,格柵層數越多變形越小,填筑時壓縮變形量加筋區3>加筋區2>加筋區1,從而使加筋區3 擠壓加筋區2,加筋區2擠壓加筋區1。擠壓力qAE和qBF使加筋區1產生向下的土拱效應,使其中部出現應力峰值,并大于土體自重計算值。同理,擠壓力qBF和qCG使加筋區2 產生向下的土拱效應,使其中部產生應力峰值。臨近返包體的基底垂直應力相對較小,是由于返包格柵的網兜效應產生對其上覆填土的托舉力和外加返包體對臨近填土向上的摩擦力fAE導致的。
圖7給出了從填筑開始到工后一段時期擋墻基底距返包體不同距離處垂直應力隨時間的變化曲線。由圖7可知:填筑期,由于上覆填土的增加,基底垂直應力隨填筑時間的增加而增大;填筑完成之后,返包體后基底垂直應力隨時間而下降,遠離返包體區域的基底垂直應力隨時間而上升;填筑完成直到面板澆筑后的一段時間,由于土體的回彈,格柵發生收縮,返包格柵被拉緊,從而對其上覆填土的托舉力增強,致使返包體后基底垂直應力下降;格柵收縮,格柵網兜效應產生的合力F1和F2減小,從而基底其他部位垂直應力增大;經過2 次地震,基底垂直應力略有增長,最大增長4.9%。由于通鋪格柵的對拉作用,使兩側擋墻形成穩定的整體結構,對墻內土體進行有效圍箍;發生地震后,由于地震波的沖擊,使墻內土體整體趨于密實,從而使基底垂直應力增長。
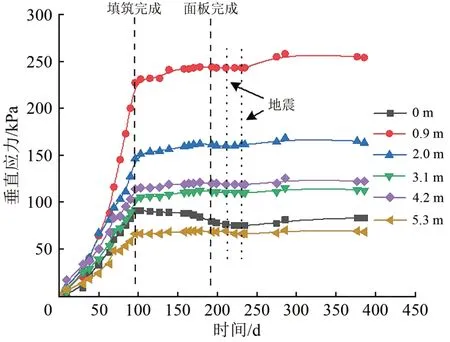
圖7 距返包體不同距離處基底垂直應力隨時間變化曲線
4.2 返包體背部土壓力
圖8—圖11分別給出了返包體背部水平土壓力、垂直土壓力隨填筑高度的變化曲線及填筑完成后沿墻高的分布曲線(圖9、圖11中時間以面板施工完成開始計算)。
由圖8—圖11可知如下結果。
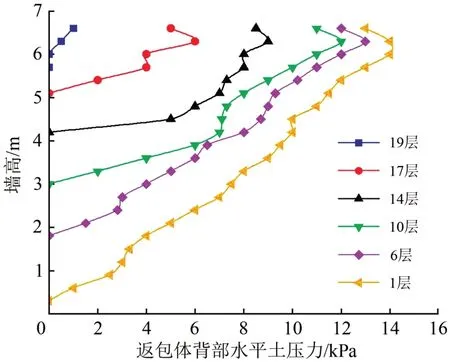
圖8 填筑時返包體背部水平土壓力隨填筑高度變化曲線
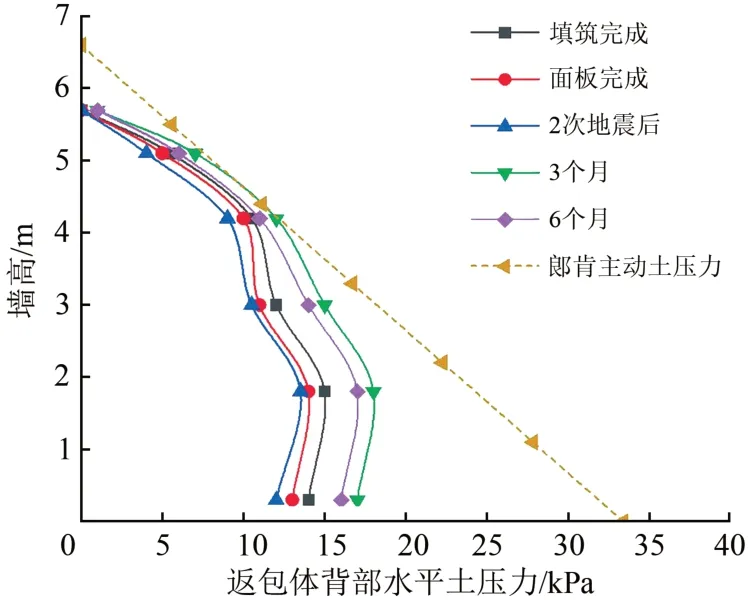
圖9 填筑完成后返包體背部水平土壓力沿墻高分布曲線
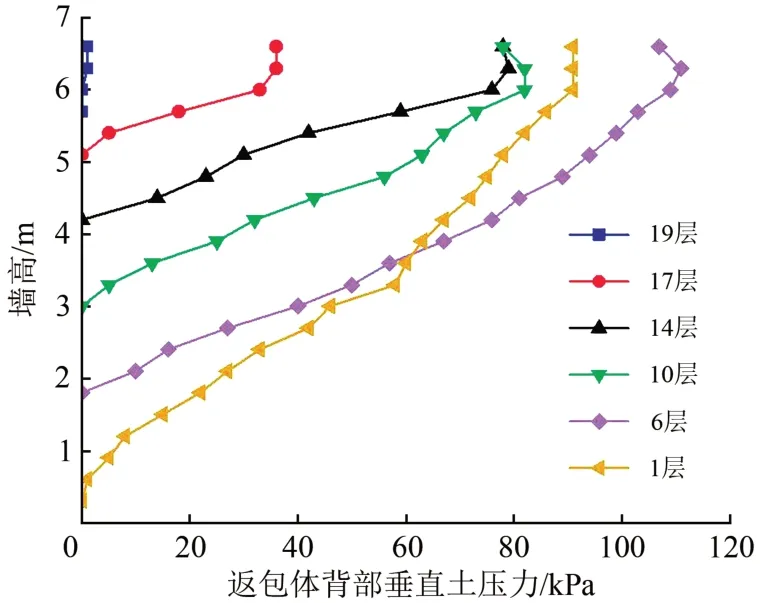
圖10 填筑時返包體背部垂直土壓力隨填筑高度變化曲線
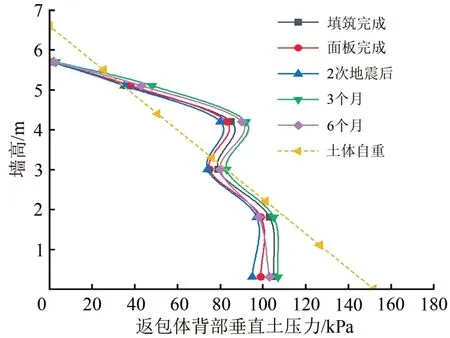
圖11 填筑完成后返包體背部垂直土壓力沿墻高分布曲線
(1)施工期,返包體背部水平土壓力和垂直土壓力隨填筑高度的增加而逐漸增大,增加速率逐漸降低,最后土壓力有減小的趨勢。土壓力增長速率降低直至減小,主要由于在填筑過程中3個區域產生一定的壓縮量,對返包體產生擠壓作用。在土體擠壓作用下,返包體產生水平位移,使土壓力得到釋放。
(2)施工完成后,返包體背部水平土壓力和垂直土壓力沿墻高呈非線性分布。擋墻上部水平土壓力實測值接近郎肯主動土壓力計算值,下部小于計算值,面板澆筑完6 個月后實測值為計算值的37.6%~90.6%。垂直土壓力實測值接近或大于土體自重計算值,面板澆筑完6個月后實測值為計算值的71.1%~163.0%。在面板澆筑前,主要靠返包體作為臨時面板,填筑體并非整體結構,每層加筋土作為獨立結構存在,由于每層結構的獨立性,返包體產生不同的水平位移,不同高度處返包體背部土壓力得到不同程度釋放,再加上返包格柵拉力Ti和側向摩擦力fAE的作用,使土壓力分布呈非線性。擋墻上部填筑時間短,返包體產生位移相對較小,使其實測值接近或大于計算值,擋墻下部填筑時間長,返包體產生位移相對較大,使其實測值小于計算值。返包體背部土壓力較大,可增強背部填土的剛度和強度,有效減小墻體的水平變形,增加擋墻整體穩定性。
(3)發生2 次地震后,擋墻整體沉降增加,墻面板外移,水平土壓力減小3.6%~20.0%,豎直土壓力減小2.0%~7.9%。隨后,返包體背部土壓力有所增長,主要因為此段時間墻面板有所內傾,并且擋墻為雙側對拉的穩定結構,在墻后土體固結沉降過程中,土壓力增大。
4.3 土工格柵應變
圖12—圖17分別給出了第2,6,10,14,17和20層土工格柵應變分布曲線。
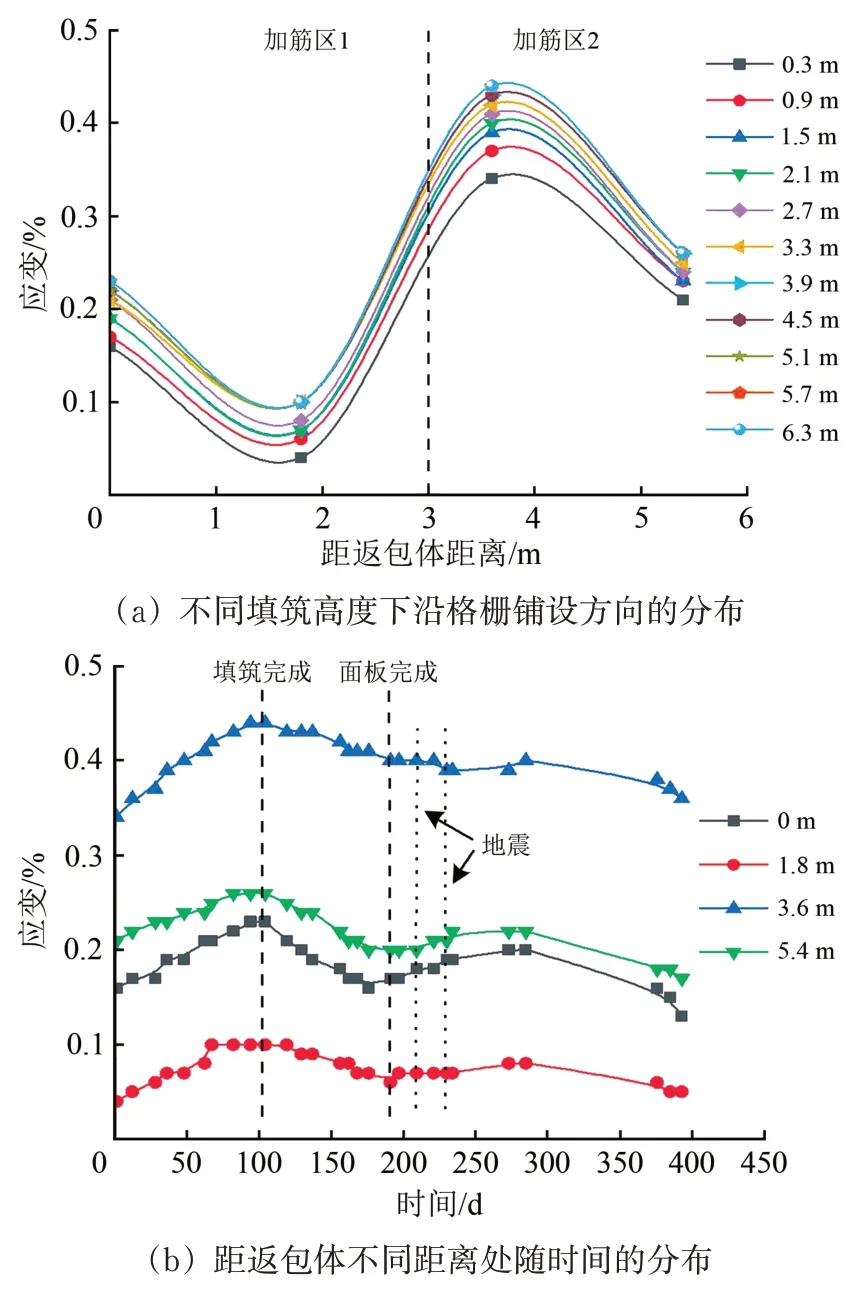
圖12 第2層土工格柵應變分布曲線
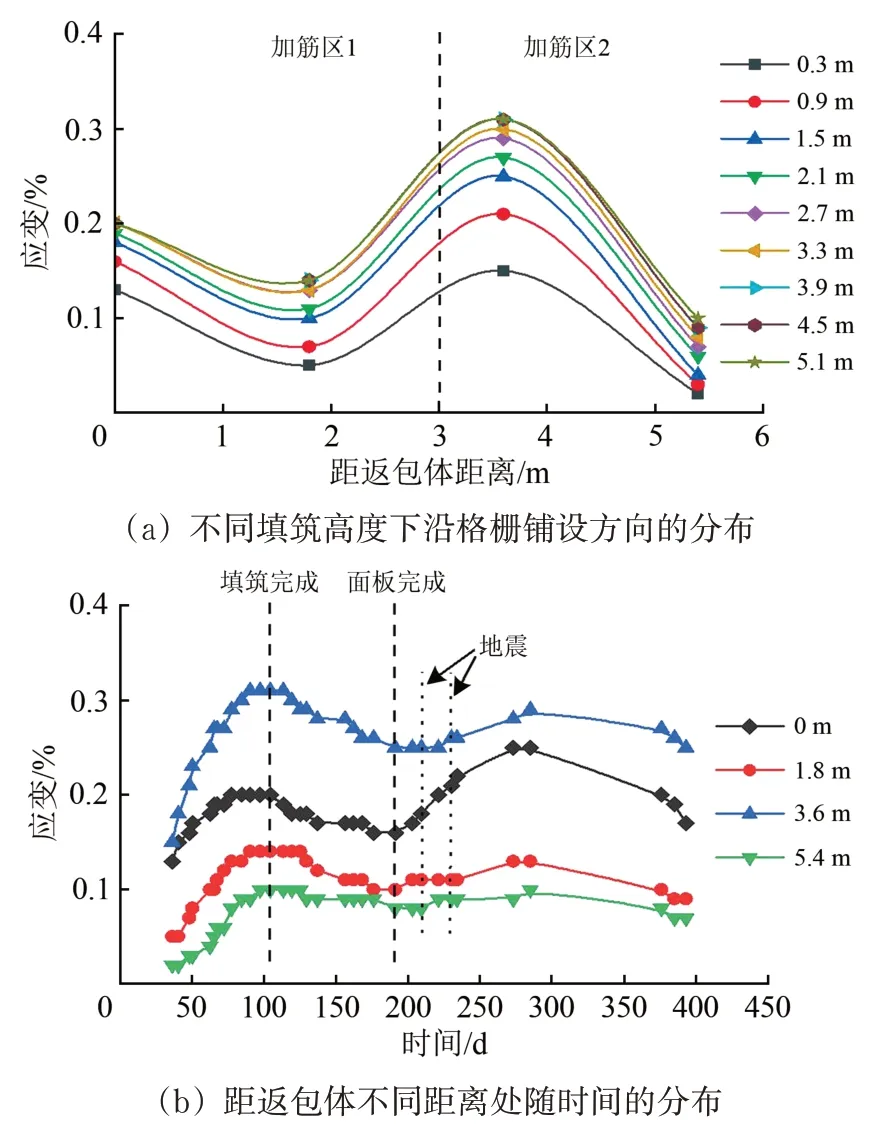
圖13 第6層土工格柵應變分布曲線
由圖12—圖17可知如下結果。
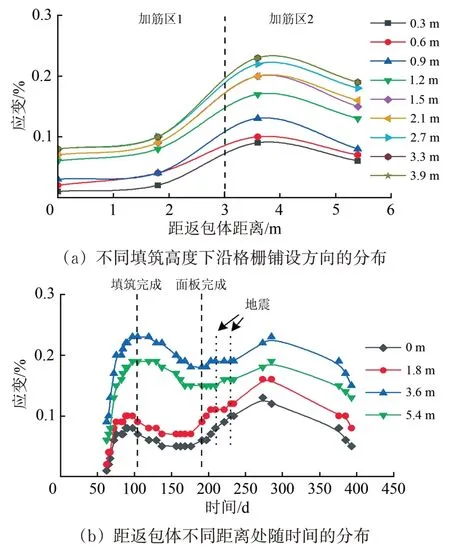
圖14 第10層土工格柵應變分布曲線
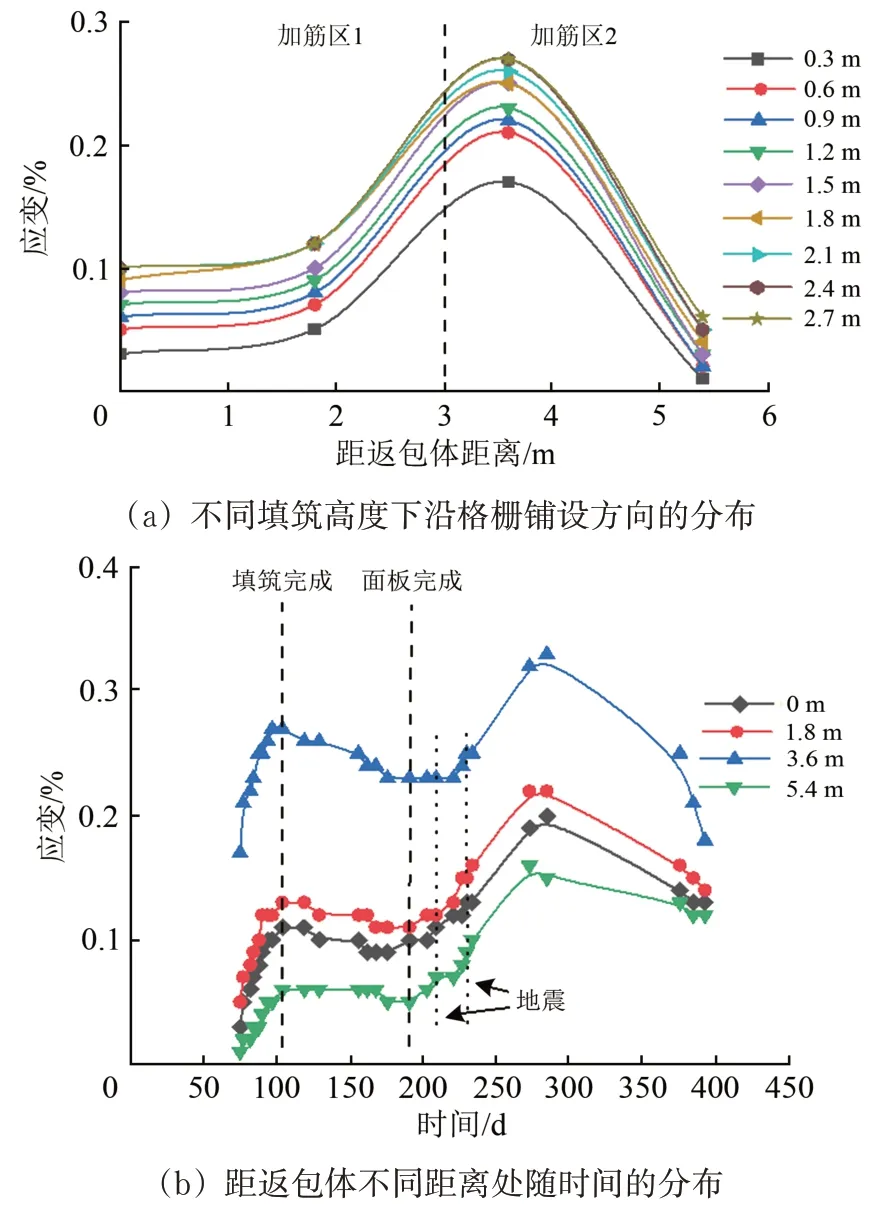
圖15 第14層土工格柵應變分布曲線
(1)每層土工格柵沿格柵鋪設方向呈非線性分布。第2 和第6 層土工格柵應變呈現雙峰,峰值出現在距返包體0 和3.6 m 處。第10,14,17 和20層土工格柵呈單峰,峰值出現在距返包體3.6 m處。0 m 處出現峰值主要是因為返包體基底與加筋區1 基底存在差異沉降,使格柵拉力TAEi和Ti增加,從而應變增加。3.6 m 處出現峰值主要是因為加筋區2 和加筋區1 存在差異沉降,且加筋區2 內部由于兩側的擠壓產生向下的土拱效應,增加了加筋區2 格柵拉力TBFi,從而應變增加。加筋區1 時雙層格柵承受拉力,加筋區2 是單層格柵承受拉力,所以應變峰值主要出現在加筋區2。
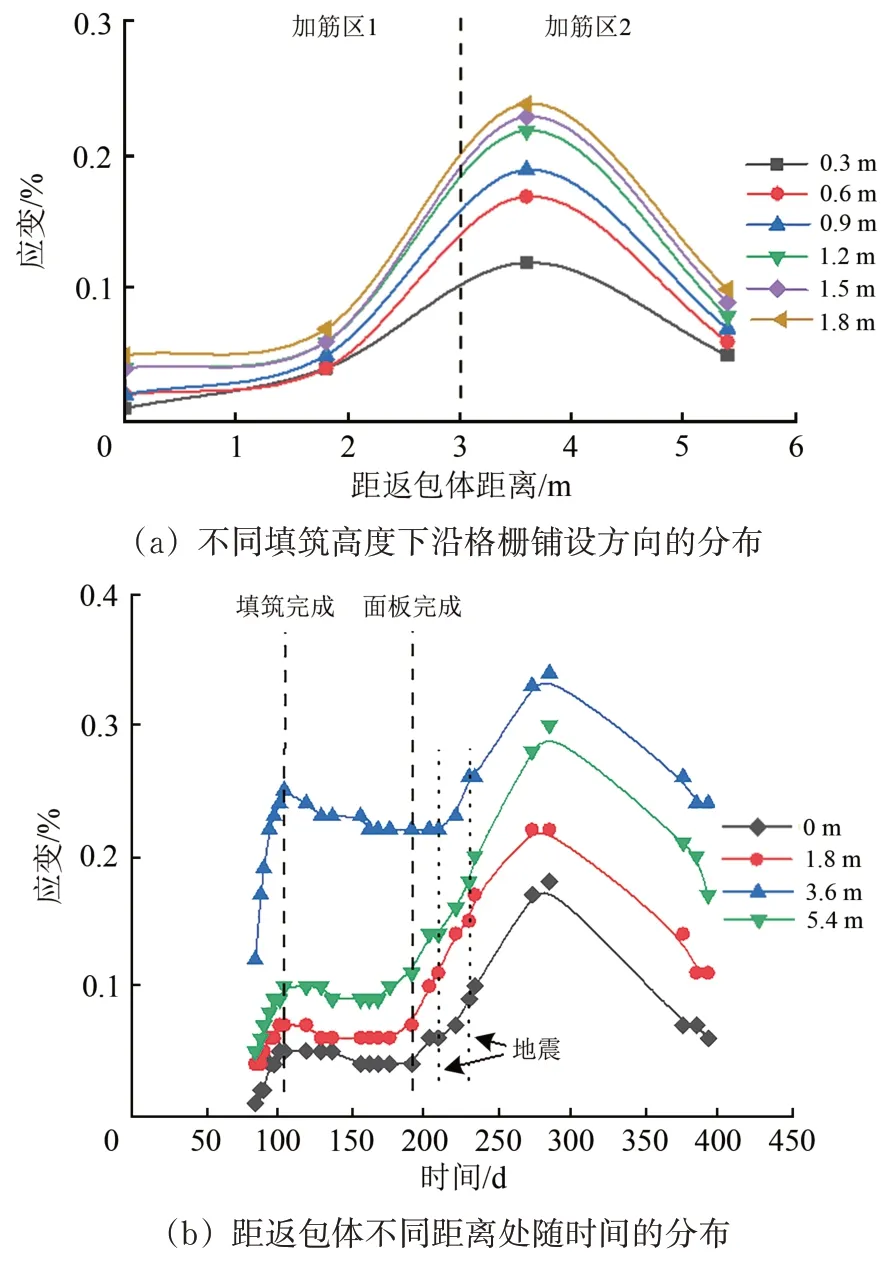
圖16 第17層土工格柵應變分布曲線
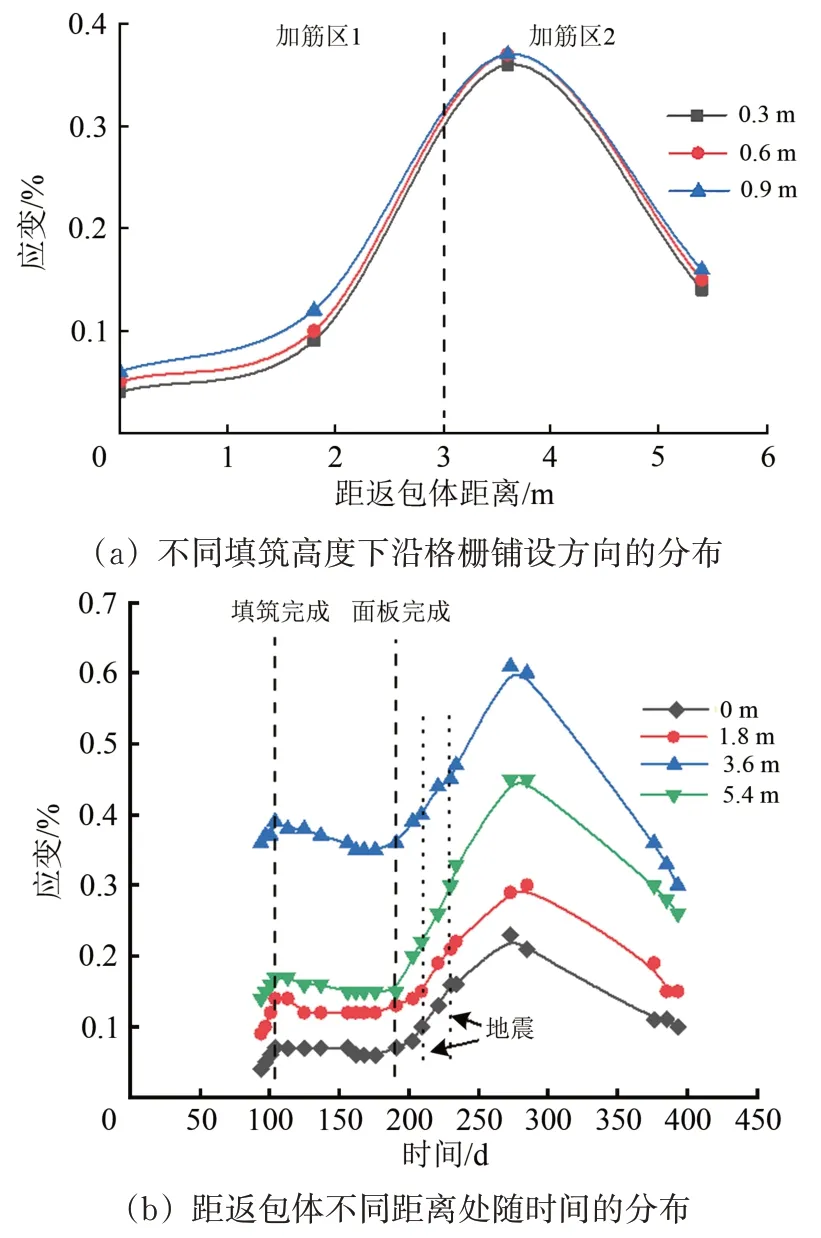
圖17 第20層土工格柵應變分布曲線
(2)每層格柵應變隨著上覆填土高度的增加而增大,而后應變增長速率逐漸減小,格柵應變增長速率由20%逐漸降至3.6%。填土所產生的垂直應力通過每層格柵時由于格柵的網兜效應而產生應力重分布并有所減小。格柵層數越多,上覆填土產生的垂直應力到達相應格柵層時削弱也就越強,格柵應變的增長速率也就越小。
(3)從墻體底層到頂層,格柵應變隨時間變化的速率逐漸增大,從第2 層至第20 層,應變變化率最大值從0.02% d-1升至0.35% d-1。主要是因為擋墻下部土體隨著上覆填土的增多及時間的增加,逐漸壓密固結,使處于下部的格柵應變變化速率小。而擋墻高度越高,土體壓密程度越低,格柵的應變變化速率越大。
(4)格柵應變隨時間呈雙峰變化,墻體內格柵最大應變值為0.66%,遠小于格柵峰值應變,亦小于文獻[16—18]中所研究的其他類型擋墻的格柵應變。土體填筑瞬間,土工格柵產生瞬間彈性變形。填筑完成到面板澆筑完成,土體內部發生回彈,格柵產生微量收縮,格柵應變相對填筑完成時減小了14%~26%。面板澆筑完成后,由于2次地震產生的瞬時地震波增加了土體的密實度,使格柵應變增長了2.6%~32%;達到峰值后格柵應變降低可能是因為地震荷載產生的土體壓密作用使格柵應變到達一定值后,格柵產生了應力松弛,或者因為此段時間墻體內部溫度降低,從而導致格柵收縮。
4.4 基底及墻頂沉降
圖18給出了填筑期基底沉降隨填筑高度變化。由圖18可知:
(1)隨著填筑高度的增加,基底沉降逐漸增加,且增加速率逐漸減小。填筑期結束,路肩基底沉降達到10.4 mm,路中基底沉降達到7.6 mm。沉降速率減小主要由2 方面原因造成:一方面,隨著時間的增長,基底及以下土層逐漸發生固結;另一方面,隨填筑高度的增加,格柵網兜效應產生的合力F1,F2和F3的增長速率分別大于土體自重W1,W2和W3的增長速率。每填筑新的1層,土體自重應力都需要多經過1 層格柵才能傳遞到基底,因此逐漸降低了填土自重應力在基底產生的影響,使其沉降速率降低。
(2)路肩基底沉降大于路中基底沉降。加筋區2 中部由于兩側擠壓力qAE和qBF的作用,產生向下的土拱效應,此處基底應力大于土體自重且大于路中基底應力,致使沉降大于路中。
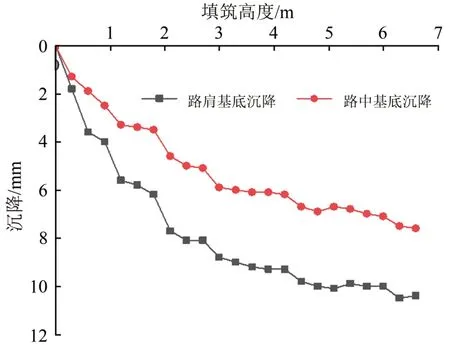
圖18 基底沉降隨填筑高度的變化
圖19給出了基底及墻頂的工后變形和墻體壓縮量。由圖19可知如下結果。
(1)擋墻施工完成后,基底沉降在5 mm 以內,遠小于墻頂沉降。這是由于基底的沉降主要發生在擋墻填筑期,填筑完成時已發生一定程度固結,工后主要為擋墻自身的固結沉降。
(2)路中墻體壓縮量大于路肩墻體壓縮量。面板澆筑完成時,路中墻體壓縮量達到7.1 mm,路肩墻體壓縮量達到4.6 mm,隨后墻體壓縮量逐漸趨于穩定。路中屬于加筋區3,只有通鋪的格柵,格柵網兜效應產生的合力F3較小,土體易發生沉降;而路肩屬于加筋區1,每層均有雙層土工格柵,格柵網兜效應產生的合力F1較大,土體不易發生沉降。
(3)面板完成前,返包體作為臨時面板,產生的水平位移較大,致使墻體壓縮量較大;面板完成后,對墻體產生了圍箍的作用,使墻體壓縮量逐漸趨于穩定。發生2 次地震后,使路中墻體壓縮量增加0.2 mm,路肩墻體壓縮量增加0.8 mm。墻體壓縮量略有增大主要是由于地震波的震蕩作用使土體密實,并使孔隙水壓力消散,而后產生固結沉降所致。
4.5 墻面水平位移
圖20給出了擋墻面板澆筑完成后,不同時期的墻面水平位移。由圖20可知:在面板澆筑完成后,墻面位移極小,總體在1 mm 范圍之內。發生2 次地震后,面板發生外移,位移最大值為0.26 mm。達到3 個月時,面板發生了內傾,主要由于面板和返包體組合和加筋區1的基底差異沉降所造成。隨后,當S3與S1和S2三角夾層區域中的土體壓實度趨于穩定后,由于墻體壓縮,面板再次發生外移。

圖19 工后沉降與墻體壓縮量
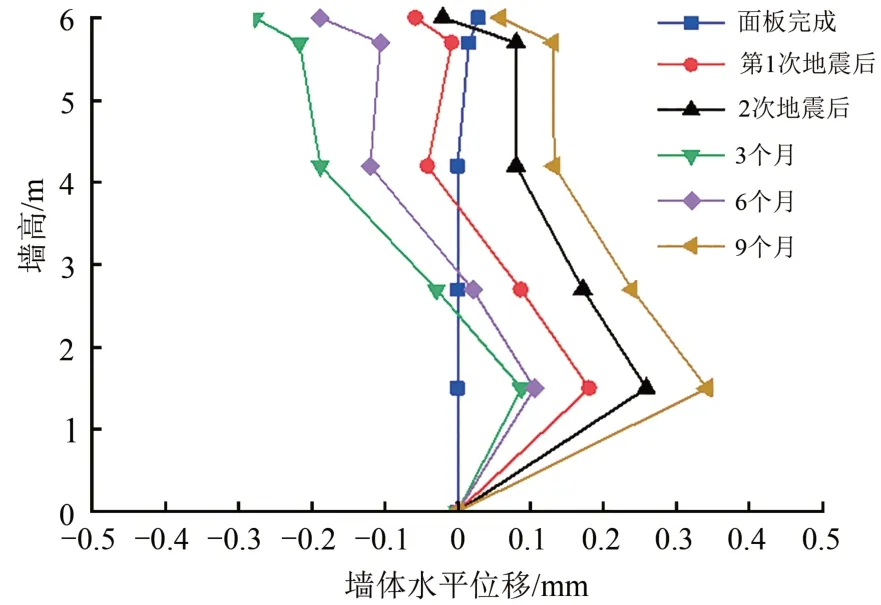
圖20 墻面水平位移
5 結 論
(1)基底垂直應力沿筋長方向呈雙峰分布,峰值分別出現在加筋區1 中部和加筋區2 中部。靠近返包體處基底垂直應力隨時間而下降,其余部位基底垂直應力隨時間而上升。
(2)返包體背部水平土壓力和垂直土壓力隨填筑高度的增加而增加。填筑完成后,沿墻高呈非線性分布。
(3)格柵應變沿筋長方向呈非線性分布。其隨時間呈雙峰變化,且沿墻高方向變化速率逐漸增大。
(4)面板完成后,墻體壓縮量變化速率減小,路中墻體壓縮量大于路肩墻體壓縮量。墻面水平位移極小,在1 mm范圍之內。
(5)擋墻的抗震性能良好。地震后,其基底垂直應力最大增長4.9%,返包體背部水平土壓力減小3.6%~20.0%,豎直土壓力減小2.0%~7.9 %;格柵應變增加2.6%~32%;路中墻體壓縮量增加0.2 mm,路肩墻體壓縮量增加0.8 mm;墻面板外移0~0.26 mm。

