福建成品油管道停輸后壓力預測算法模型

邵曉 鄭堅欽 戴元豪 張揚

1中國石化福建石油分公司

2中國石油大學（北京）

成品油管道的停輸操作是管道在投產和運行過程中不可避免的[1]。停輸時段的管道管理和安全監控也是必不可少的。在福建成品油管道停輸期間，現場人員對于管內壓力變化無法提前預測，當管內壓力下降時，經常誤以為是管道發生泄漏或出現打孔盜油事故，需現場人員巡檢排查[2]，不僅增加了現場人員的工作量，也不利于控制運行成本。因此，有必要對管道建立停輸時段壓力變化模型，提前預測管內壓力變化，監測管道停輸狀態。當檢測值與預測值差別不大時，可以認為管內壓力屬于正常變化；而當兩者差別較大時，很大可能發生泄漏等異常事故，應立即排查，保證管道安全。

目前，國內針對成品油管道停輸的研究較少[3]，還沒有建立停輸時段管內壓力變化的預測模型。隨著我國成品油管道的快速投產和運行，對多條管道開始分析其停輸的壓力變化[4]。郭袆等[5]針對港棗成品油管道在計劃停輸期間頻繁出現管內壓力迅速下降的問題，根據管道相關數據，分別研究了溫度對管內油品體積和管道壓力的影響程度，結果表明油品溫度的下降是導致管道停輸壓力出現下降的主要原因。陳春[6]研究了江陰—無錫成品油管道停輸后壓力變化情況，基于傳熱學和熱力學理論，結合現場實際數據，建立油品壓力溫度變化模型，通過仿真模擬，提出修正系數，改進管道停輸壓力變化模型。

目前研究主要存在兩個問題：①依托管內壓力、溫度變化的經驗公式，建立機理模型或數值模擬來探究壓力變化情況，由于現場環境的不確定性，模型與實際情況存在差別；②將環境溫度設為定值，一定程度上影響模型的準確性。

福建成品油管道的泵出站口都設有溫度計和壓力表，已儲存大量的停輸管道數據。如何挖掘這些數據之間的規律，通過關聯分析建立停輸壓力變化模型是現場管理人員目前思考的方向。隨著人工智能和大數據時代的來臨，基于數據驅動的機器學習算法在預測模型上發揮越來越重要的作用[7]。韓小明等[8]基于人工神經網絡機器學習理論，建立油氣管道完整性預測模型，提高了管道安全管理水平。胡群芳等[9]基于模型參數的概率分布，利用貝葉斯理論對燃氣管道建立腐蝕深度預測模型，定量評估腐蝕安全問題。張新生等[10]基于現場實測數據和馬爾科夫鏈模特卡洛算法，建立油氣管道剩余壽命預測模型，應用于管道的可靠性評價中。

因此，本文將基于福建成品油管道已有的大量停輸溫度壓力數據和目前流行的機器學習算法，針對管道出站檢測點建立停輸壓力變化預測模型，監測管內壓力變化情況。

1 管道停輸機理分析

目前研究表明，由于成品油管道通常采用常溫密閉輸送方式，而管內油品具有膨脹性和壓縮性的物理特性，基于傳熱學理論，管輸油品和管道環境溫度的差異是引起管道壓力變化的主要因素。在管道停輸初始階段，由于管內油品溫度明顯大于環境溫度，油品與管壁、管壁和土壤之間的熱交換較強，管內油品下降速度快。隨著停輸時間的增加，油品與環境溫差減小，管內溫度下降速度隨之減小。管道停輸后油品溫度隨時間的變化已形成經驗公式(1)[11]。當管道開始停輸時，出站檢測點可獲取初始油溫，以小時為單位，可以根據公式(1)求出停輸一段時間后的管內油溫變化。

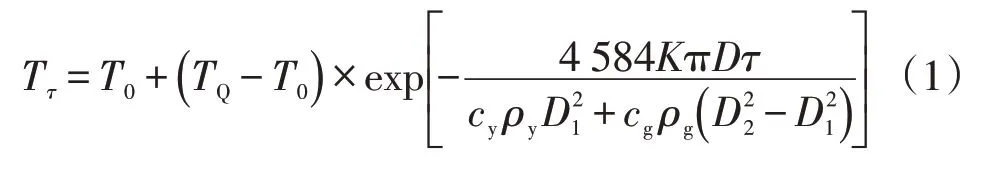
式中：K為總傳熱系數，W/(m·℃)；D、D1、D2為管道平均直徑、管道內徑和管道外徑，m；cy、cg為油和鋼材的比熱容，J/(kg·℃)；ρy、ρg為油和鋼材的密度，kg/m3；T0為環境溫度，℃；Tτ為停輸τ小時后的油溫，℃；TQ為開始停輸時的油溫，℃；τ為停輸時間，h。

油溫和管道環境的差異，使得管內油品體積發生一定程度的變化，從而導致管內壓力的變化。隨著油溫的變化，管內壓力的變化形成的經驗公式為

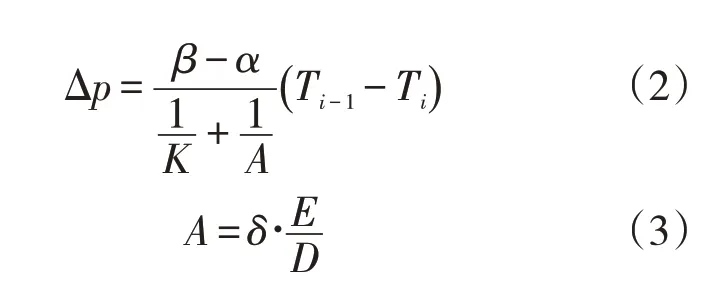
式中：α為管道的體積膨脹系數，管道為鋼管時，α≈3.3×10-5℃-1；δ為管道壁厚，mm；E為管材的楊氏彈性模量，管道為鋼管時，E≈2×1011Pa；β為油品的體積膨脹系數，℃-1；K為油品的彈性系數，Pa；Ti為第i時步的油溫，℃；Ti-1為第i-1時步的油溫，℃；Δp為第i時步與第i-1時步的壓差，Pa。

由經驗公式（1）和（2），可以得出管道壓力變化的影響因素分為兩類：一類是管道與土壤的固有屬性，這些因素基本保持不變，在建立預測模型時可以當成參數，不考慮在內；另一類是可變因素，分別為停輸時間τ、初始油溫TQ、環境溫度T0。在前人的研究中，環境溫度一般取平均環境溫度。但由于不同地區晝夜溫差不同，為提高計算精度，本文通過氣象網站獲取停輸期間內每個小時的具體溫度值。通過以上分析，確定影響Δp的變量為τ、TQ和T0，因此，下面將建立基于τ、TQ和T0的壓力預測回歸模型。

2 建立管道停輸壓力預測模型

2.1 數據預處理

現場可通過管道運行系統導出停輸時段各出站點的壓力、油溫和停輸時間，缺少的是環境溫度。借助爬蟲技術在天氣網站上獲取各地區的歷史溫度，整理數據并建立停輸管內壓力變化預測數據庫。

數據歸一化是數據處理中非常重要的一步，其可以加快訓練模型的收斂，提高預測精度。由于p以及變量τ、TQ和T0的取值范圍不同，為了消除各變量之間的幅度影響，需要進行數據歸一化。停輸數據通過最小—最大歸一化方法處理，每個維度的數據均被歸一化為0～1范圍內，如方程(4)所示：

其中，x*為歸一化的值，xi為各變量原始值，xmax和xmin分別為各變量的最大值和最小值。

2.2 機器學習算法

（1）線性回歸（Linear Regression，LR）：線性回歸算法形式簡單，就是能夠用一個直線較為精確地描述數據之間的關系。通過輸入變量的線性組合來預測目標值，是機器學習中非常重要的基本算法。特點是易于建模，方法簡單，但無法擬合非線性關系。

（2）支持向量機（Support Vector Machine，SVM）：它是一種用于分類和回歸的監督學習算法[12]。當用于分類時，基本思想是根據現有數據樣本找到一個最大間隔的“超平面”，使得所有樣本到“超平面”的距離最大。而對于回歸預測問題，樣本點最終只有一類，通過設定閾值計算損失，目的是使得所有數據的類內方差最小。

（3）決策樹回歸（Decision Tree，DT）：就是將特征空間劃分成若干單元，每一個劃分單元有一個特定的輸出。劃分的過程也就是建立樹的過程，每劃分一次，隨即確定劃分單元對應的輸出，也就多了一個結點。當根據停止條件劃分終止的時候，最終每個單元的輸出也就確定了，也就是葉結點[13]。

（4）隨機森林（Random Forest，RF）：它是指利用多棵決策樹對樣本進行訓練并預測的一種算法，是一種集成學習算法[14]。通過對樣本集自主采樣和隨機選擇子集用于節點分割方式構建多個決策樹，每次分裂時選擇最好的特征進行分裂。最終通過所有決策樹的均值確定預測結果。

（5）梯度提升（Gradient Boosting，GB）：它也是一種以決策樹為基學習器構建的集成學習算法[15]。利用最速下降方法，即利用損失函數的負梯度在當前模型的值，不斷迭代、不斷構造回歸樹進行決策，而且每一個回歸的樣本數據均來自上一個回歸樹所產生的殘差，主要目的是降低偏差。

2.3 模型評價指標

為了評估不同機器學習算法的預測效果，本文采用判定系數(R2)、平均絕對誤差(MAE)和均方根誤差(RMSE)作為預測模型的性能指標。即

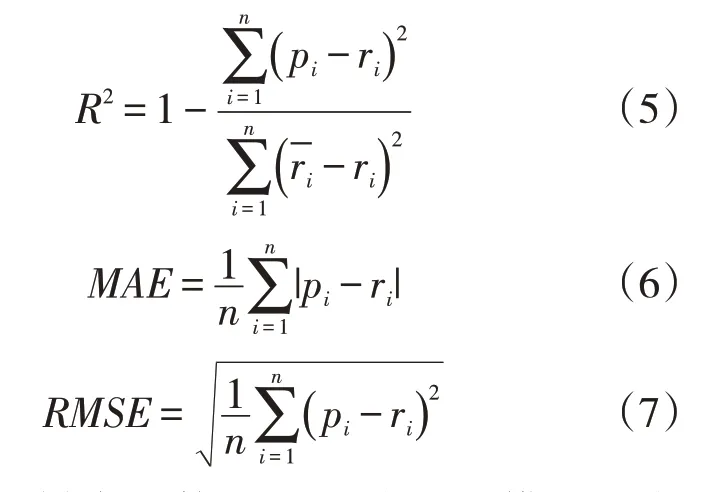
其中，n為數據樣本的數量；pi為預測模型壓力輸出值；ri為原始壓力值。

3 現場驗證

3.1 泉港南線出站點

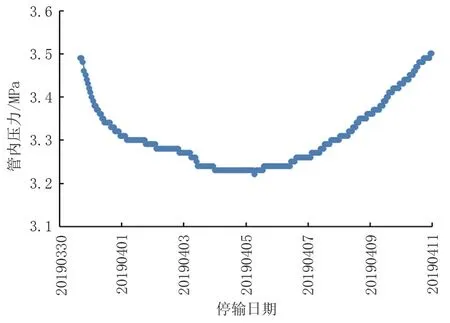
圖1 泉港南線出站管內壓力隨停輸時間的變化情況Fig.1 Change of the pipeline pressure of Quangang South Station Outgoing Line with shutdown time

以福建成品油管道在2019年3月30日到4月11日停輸期間泉港南線出站壓力變化為例，壓力變化如圖1所示，部分數據如表1所示。為了提高預測模型的準確性，打亂樣本數據并劃分數據集。訓練集、驗證集、測試集的占比分別為70%、10%、20%。5個算法在測試集上的預測結果如圖2所示，圖3展示的是不同預測模型所對應的RMSE、MAE、R2。由圖2和圖3可知，LR和SVM預測結果與真實值差別較大，特別是LR，其R2只有0.329，RMSE和MAE的值也較大。因此，這兩種回歸預測模型不適合用于該管道的壓力變化預測。對于DT、RF、GB，預測曲線與真實曲線幾乎重合，RMSE和MAE的值都小于0.05。另外三者的R2也都大于0.970，其中RF的值最大，為0.981。預測結果說明DT、RF、GB模型適用于福建成品油管道停輸的管內壓力變化分析。

表1 泉港南線出站點部分數據樣本Tab.1 Data sample of the outgoing point in Quangang South Line Station

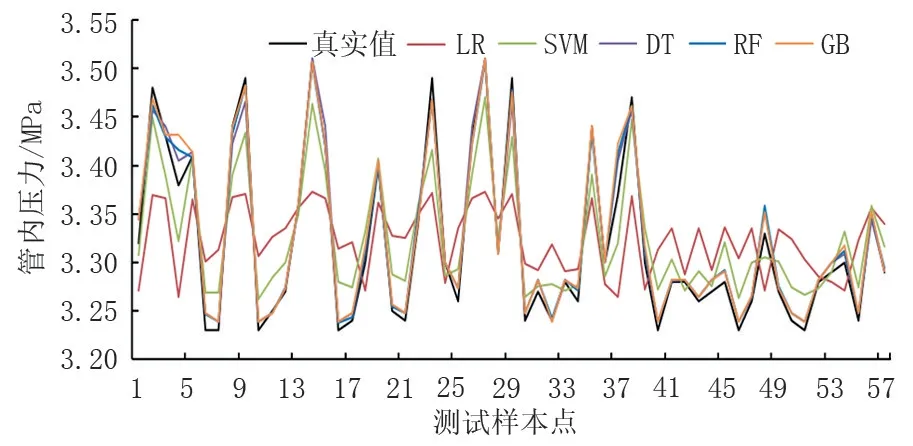
圖2 不同預測模型在泉港南線出站測試集上的預測結果Fig.2 Prediction results of different prediction models in the outgoing test set of Quangang South Line Station

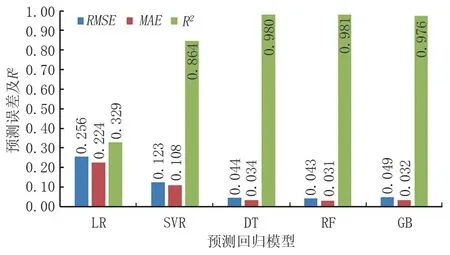
圖3 不同預測模型在泉港南線出站點的預測效果對比Fig.3 Prediction effect comparison of different prediction models in the outging point of Quangang South Line Station

3.2 黃塘溪東出站點

同樣，以黃塘溪東出站點在2019年5月5日到19日停輸期間壓力變化為例，壓力變化如圖4所示。5個算法在測試集上的預測結果如圖5所示，圖6展示的是不同預測模型所對應的RMSE、MAE、R2。由圖5和圖6可知，LR和SVM預測結果與真實值差別較大，不適合用于該管道的壓力變化預測。對于DT、RF、GB，其預測曲線與真實曲線十分相近，RMSE和MAE的值也都小于0.05。但DT的R2為0.953，小于RF的0.988和GB的0.975，因此RF的預測效果最佳。結合上述分析可知，DT、RF、GB模型適用于福建成品油管道停輸的管內壓力變化預測，其中RF準確度最高。

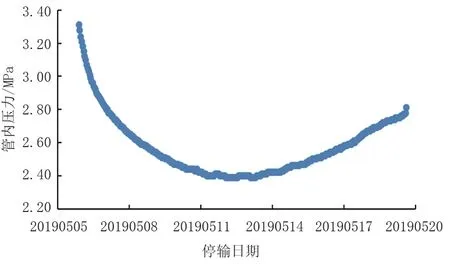
圖4 黃塘溪東出站管內壓力隨停輸時間的變化情況Fig.4 Change of the pipeline pressure of Huangtangxi East Station Outgoing Line with shutdown time

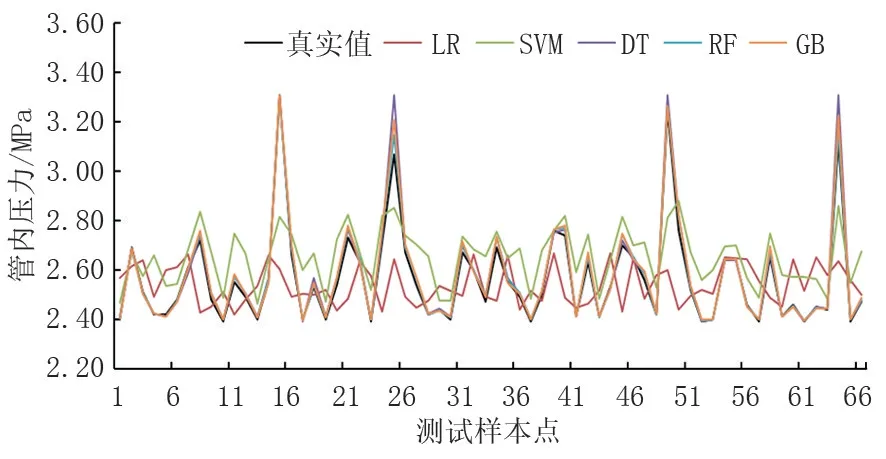
圖5 不同預測模型在黃塘溪東出站測試集上的預測結果Fig.5 Prediction results of different prediction models in the outgoing test set of Huangtangxi East Station

圖6 不同預測模型在黃塘溪東出站點的預測效果對比Fig.6 Prediction effect comparison of different prediction models in the outgoing poin of Huangtangxi East Station

4 結論

針對福建成品油管道停輸再啟動過程中管內壓力變化無常的問題，建立了基于LR、SVM、DT、RF、GB的5種機器學習算法的壓力預測模型，模型評價指標為RMSE、MAE、R2。以泉港南線和黃塘溪東出站為例，預測結果表明DT、RF、GB的R2可達到0.950以上，模型預測準確度高，可適用于福建成品油管道停輸的管內壓力變化分析。基于天氣預報氣溫數據，該模型可預測未來時段管內壓力的變化趨勢，指導現場運行管理。該研究在其他成品油管道上同樣具有運用的可能性。對于特定的成品油管道，通過獲取現場的停輸數據和當地的溫度數據，即可代入建立的壓力預測模型。但由于不同管道數據的差異性，最終得到的模型參數及效果會有所不同。