發電機單相短路時電磁轉矩諧波特性分析

辛 鵬，劉亞丹

(吉林化工學院 信息與控制工程學院，吉林 吉林 132022)

隨著電力技術的發展，發電機單機容量不斷增大，機組的安全穩定運行對于電力系統而言越發重要.同時機組一旦發生故障，對機組自身也可能造成不可逆的損害，并威脅到人員安全[1-3].

近年來，國內外學者對于發電機的安全穩定問題進行了廣泛的研究.文獻[4]研究了同步發電機定子繞組匝間短路故障時瞬態電磁轉矩特性.文獻[5]研究了發電機定子繞組故障特征規律，并構建了故障預測模型.文獻[6]提出一種改進矢量擬合算法研究轉子繞組匝間短路.文獻[7]研究了感應電動機單相短路時轉子齒部電磁力分布以及轉子電磁力波動變化特征.文獻[8]采用有限元法研究了雙饋風力發電機超同步、亞同步、同步正常運行、定子繞組匝間及單相短路故障等多種工況下機組的電磁特性.

本文以一臺核電機組為研究對象，采用場-路耦合法建立了仿真模型.對發電機帶額定負載穩態運行時，機組發生單相對地短路故障進行仿真分析，得到了機組故障前后氣隙磁場及電磁轉矩的變化特征.

1 場路耦合模型

1.1 發電機有限元模型

假設鐵芯材料磁導率各向同性，電機內的磁場為似穩場.忽略位移電流及定子鐵芯渦流損耗，則電機內二維瞬態場的邊值問題為：

(1)

式中：μ為磁導率；J為源電流密度；σ為電導率；A為矢量磁位；為定子外圓與轉子內圓邊界.

1.2 定子回路方程

發電機定子回路方程可表示為：

(2)

式中：Us=[uA,uB,uC]T；Es=[eA,eB,eC]T；Is=[iA,iB,iC]T；Rs，Ls為定子電阻及端部漏感矩陣；Rs=diag[Rs,Rs,Rs]；Ls=diag[Ls,Ls,Ls]；lef為電機軸向有效長度；Cs為定子電流的關聯矩陣.

定子繞組電流密度為：

(3)

式中：is為定子繞組相電流；a為定子繞組并聯支路數；Ss為定子線圈截面積.

1.3 勵磁繞組耦合電路方程

(4)

式中：uf為發電機勵磁繞組電壓；ef為勵磁繞組感應電勢；if為勵磁電流；Rf、Lf為勵磁繞電阻及端部漏電感；Cf為勵磁電流的關聯矩陣.

勵磁繞組電流密度為：

Jf=if/sf

(5)

式中：sf為勵磁繞組截面積.

1.4 阻尼回路方程

設槽楔與阻尼條直線部分電流密度為Jci、Jzi,則：

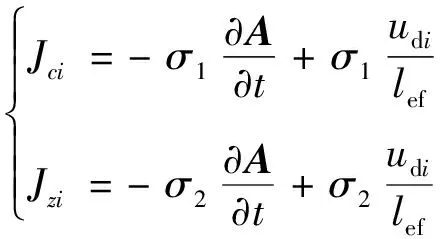
(6)

式中：σ1、σ2分別為槽楔和阻尼條電導率；udi為阻尼條兩端電壓.

由文獻[9]可知，阻尼回路方程可表示為：

(7)

式中：Ud=[ud1…udi…udk]T；Id=[id1…idi…idk]T.

1.5 轉子鐵芯渦流

對于汽輪發電機而言，其轉子為實心式，因此，可采用修正鐵芯直線部分電導率的方法對其進行處理[10].

(8)

式中：σR為轉子材料電導率.

將(3)、(5)、(6)和(8)代入(1)，經有限元離散可得：

(9)

將方程(2)、(4)、(7)、(9)耦合，消去中間變量，可得場-路耦合時步有限元方程為：

(10)

2 仿真建模及分析

本文以一臺1 407 MVA核電半速汽輪發電機額定運行狀態為研究對象，建立了場-路耦合仿真模型.發電機主要參數如表1所示，核電機組剖分后有限元模型如圖1所示.

表1 核電半速汽輪發電機主要參數

圖1 核電機組剖分截面圖

本文以發電機單機帶額定負載穩定運行為研究對象，在發電機穩定運行2.5 s后，機端發生單相短路故障，故障前后氣隙磁密結果如圖2所示.

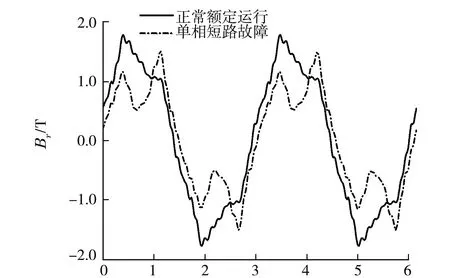
氣隙周長/m

從圖2的仿真結果可以看出，相比于額定負載運行時，故障后氣隙磁密發生了明顯的畸變，該畸變將對電磁轉矩產生一定的影響.電磁轉矩仿真結果如圖3所示.

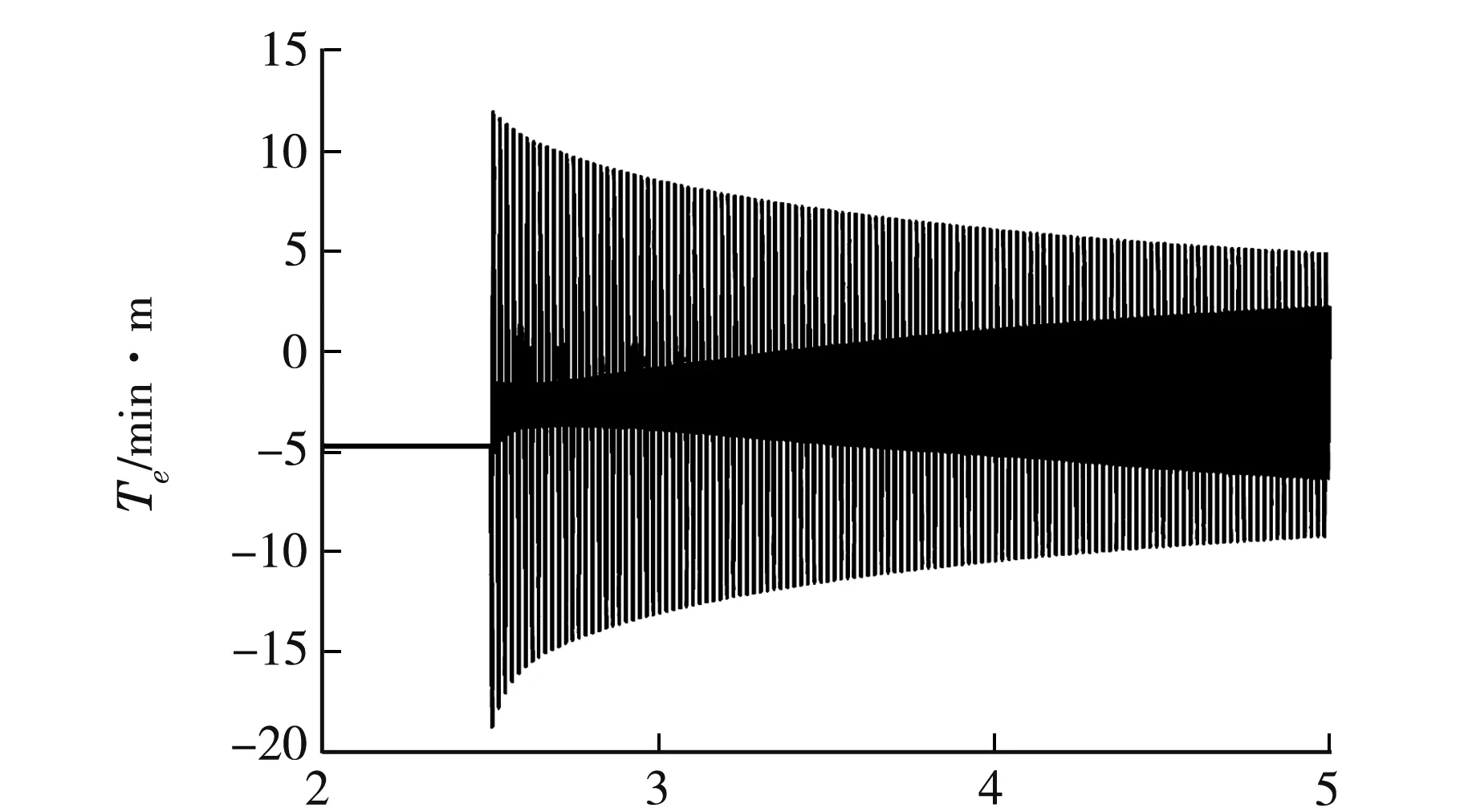
t/s

從圖3的仿真結果可以看出，故障后的電磁轉矩中除了正常運行時的直流分量外，還產生了交流分量.對電磁轉矩進行諧波分析，分析結果如圖4所示.

f/Hz

通過圖4電磁轉矩的諧波分析結果可以看出，該交流分量為偶數次諧波分量，且2倍頻諧波分量數值較大，同時電磁轉矩直流分量小于故障前的.這是由于故障后的短路電流大于正常運行時的電流，受電樞反應影響，故障后去磁效果加強，導致故障后氣隙磁場數值減小，這與圖2的仿真結果相吻合，進而導致電磁轉矩直流分量減小.此外，由于該故障為非對稱性故障，故障后定子繞組將會產生負序電流，該負序電流產生的磁場與轉子轉速同步，但旋轉方向相反，因此故障后會產生偶數次諧波電磁轉矩.

3 結 論

本文采用有限元方法，對發電機帶額定負載穩態運行時出口發生單相短路進行了仿真研究，研究結果表明，故障后氣隙磁場發生了明顯的畸變，電磁轉矩除了正常運行時的直流分量外，還產生了較大的偶數次諧波分量，同時故障后直流分量數值小于故障前的.