列車延誤條件下城市軌道交通跳停方案研究*

戶佐安 夏一鳴 鄭 磊

(西南交通大學交通運輸與物流學院1) 成都 611756)(西南交通大學綜合交通大數據應用技術國家工程實驗室2) 成都 611756)

0 引 言

城市軌道交通列車的正常運行容易因各類突發事件產生延誤，而較長時間的延誤則會導致列車大面積晚點和站臺乘客滯留.在這種情況下，常規的站站停運行調整模式已經不能很好地滿足盡快恢復列車正常運行的要求[1].而跳停調整模式相較于站站停調整模式，能夠使列車通過跨站運行從而更快地恢復至計劃運行狀態，但同時也會導致部分乘客無法及時乘降，增加其乘車及候車時間.現階段城軌列車跳停方案的制定主要還是依據于調度員經驗及預案，在全局性上還存在不足.因此，為了制定更為合理的跳停方案，在恢復列車正常運行的同時盡可能縮短乘客的旅行時間，建立行之有效的列車運行調整模型和相應求解算法就具有十分重要的意義.

國內外學者針對城市軌道交通列車跳停問題已展開一定的研究.鄭鋰等[2]對列車停站方案進行分類組合，建立了以乘客總出行時間節省最大為目標的0-1規劃模型，并通過算例驗證了模型的有效性.王嬋嬋等[3]從延誤情況下多線換乘站的工況、跳停需求、跳停方案影響因素，以及跳停效果等方面進行分析，得出列車延誤時在多線換乘站的跳停方法，并通過實際案例分析了該方法的局限性.劉祥喜[4]對各類突發大客流的特征進行分析，選取實際案例進行客流預測，并建立了以運營效率最高為目標的停站方案優化模型，最后提出突發大客流背景下的列車運營組織策略.Cao等[5]以列車停站狀態為決策變量，建立乘客出行時間及列車總運行時間的總節省量最大為目標的0-1規劃模型，并通過實例驗證了模型的有效性.Freyss等[6]采用近似連續法將列車跳停問題用線路的站點密度等連續參數進行描述，并構建以列車運行成本最小為目標的運行調整模型，最后對跳停策略適用情況進行總結.Jamili等[7]對動態客流條件下的列車跳停方案進行研究，設計了一種將分解算法及模擬退火算法相結合的混合優化算法，并用實例證明該算法的穩定性.

綜上，現有研究大多都是針對于常規情況下的城軌列車跨站停車問題，跳停方案采用固定的列車分類組合停站模式，且沒有考慮因列車運能不足而使乘客滯留的問題.而在延誤條件下，列車之間的運行調整空間小，且站臺乘客容易出現積壓，跳停方案的制定還需要考慮列車運行安全及列車運能利用情況等等因素，因此現有研究成果并不適用于延誤條件下的列車跳停問題.本文基于某一列車延誤條件，以乘客總旅行時間最小為優化目標，考慮列車運能約束、運行約束，以及跳停約束，建立相應模型與算法，以期制定更加靈活且合理的城市軌道交通列車跳停方案.

1 問題描述

1.1 跳停影響分析

列車跳停是指載客列車抵達某站后不進行停車操作，直接運行通過此站，圖1 為列車跳停示意圖.跳停對乘客出行的影響主要體現在以下三個方面.

圖1 列車跳停示意圖

1) 跳停可以節省列車i在跳停站j的停站時間及起停附加時間，從而減少部分乘客的乘車時間.

2) 跳停會導致出行起始站為跳停站j的乘客無法及時上車，使其必須等待下一趟同向列車i+1才能上車，增加其候車時間.

3) 跳停會導致出行終到站為跳停站j的乘客無法及時下車，而乘客在提前得知跳停信息后會出現兩種選擇：①在跳停站的前一站j-1下車，此時乘客需要額外花費一次等候下一趟同向列車i+1的時間，才能到達出行終到站；②在跳停站的后一站j+1下車，此時乘客需要額外花費從跳停站j乘至后一站j+1、在站j+1等候反向列車，以及乘坐反向列車到達站j的時間.

綜上可知，跳停調整模式在提高部分乘客出行效率的同時也會對一些乘客的出行產生負面影響.因此，當某一列車發生延誤時，如何制定使整個乘客群體出行效率最高的列車運行調整方案，是本文需要解決的主要問題.

1.2 問題假設

結合我國城市軌道交通實際調度情況，本文給出以下假設.

1) 列車在線路的首站及末站均不組織跳停，列車不能連續跳停兩站，同一站點不能被連續跳停兩次.

2) 列車在恢復正點運行后不再進行調整.

3) 某線路1 h時段內的站間OD數據已知，且各站客流的到達服從均勻分布.

2 城市軌道交通列車運行調整模型

2.1 參數定義

模型相關參數定義見表1.

表1 參數定義

2.2 模型相關參數計算

本文將用列車出發時車內人數、上車需求人數、實際上車人數、實際下車人數，以及車站滯留人數來描述客流與列車運能之間的交互關系.

列車i在j站出發時的車內人數與其在j-1站出發時的車內人數及在j站的上下車人數有關，即

Pi,j=Pi,j-1+Bi,j-Ei,j

(1)

列車i在j站的實際上車人數決定于列車在該站的剩余載客能力能否滿足上車需求，以及列車在該站的跳停與否，即

(2)

式(2)中上車需求人數即為列車i-1在j站出發時的滯留人數與在時段[di-1,j,di,j]內到達j站的人數之和，為

qi,j=li-1,j+δj(di,j-di-1,j)

(3)

式(3)中j站乘客到達速率δj可由OD表中的數據直接求出，即

(4)

由跳停影響分析可知，列車i在j站的下車人數與列車i在j站、j+1站以及j-1站的跳停與否有關，即

Ei.j=(Pi,j-1·θj·ξi,j+λ1·Pi,j·θj+1·ξi,j+1·

xi,j+1+λ2·Pi,j-2·θj-1·ξi,j-1·xi,j-1)(1-xi,j)

(5)

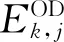
(6)

(7)

列車i離開j站時，j站滯留人數與列車i在j站面臨的上車需求人數、實際上車人數以及可能因跳停在j站提前下車的人數有關，即

li,j=qi,j-Bi,j+λ1·Pi,j·θj+1·ξi,j+1·xi,j+1

(8)

2.3 目標函數

研究目標是使乘客總旅行時間最小，乘客總旅行時間表示為T.乘客總旅行時間可分為站臺候車時間及乘車時間，分別表示為T1和T2，兩者計算為

(9)

(10)

式(9)中，第一項表示正常乘客候車時間，第二項表示滯留乘客候車時間，第三項表示乘客換乘反向列車時的候車時間，此時平均候車時間取I0/2；式(10)中，第一項表示車內乘客站間乘車時間，第二項表示列車停站過程中不下車乘客的等待時間，第三項表示乘客乘坐反向列車時的乘車時間.

優化目標即為

minT=T1+T2

(11)

2.4 運行約束

運行約束條件有：

di.j=ai,j+wj(1-xi,j)

(12)

ai.j≥di,j-1+Rj-1-τ1·xi,j-1-τ2·xi,j

(13)

ai+1,j-di.j≥I1

(14)

ai+1,j-ai.j≥I2

(15)

di+1,j-di.j≥I2

(16)

di,j≥Di,j

(17)

式(12)為停站時間約束，由于縮短停站時間可能會導致積壓的乘客無法及時乘降，因此本文不對停站時間進行調整；式(13)為列車區間運行時間約束，即列車i在j-1站跳停則可節省起動附加時間τ1，在j站跳停則可節省停車附加時間τ2；式(14)為列車最小發到間隔約束；式(15)為列車最小到達間隔約束；式(16)為列車最小發車間隔約束；式(17)為列車發車時刻約束.

2.5 跳停約束

跳停約束有：

xi.1=xi.m=0

(18)

xi.j+xi.j+1≤1

(19)

xi.j+xi+1.j≤1

(20)

式(18)為列車不能跳停首尾站；式(19)為列車不能連續跳停兩次；式(20)為同一站點不能被連續跳停兩次.

3 求解算法

目標函數及部分約束條件為非線性，而遺傳算法具有優秀的全局搜索能力及處理非線性系統優化問題的能力，因此采用遺傳算法求解[8].但由于本文決策變量中，跳停變量的取值直接決定著列車的到發時刻關系，導致兩種變量無法同時參與迭代.為解決上述問題，設計了一個內外層嵌套式遺傳算法，即外層遺傳算法對停站方案進行優化，內層遺傳算法基于外層的停站方案對到發時刻方案進行優化.具體流程見圖2.

圖2 嵌套式遺傳算法求解流程

3.1 染色體編碼及種群初始化

設外內層染色體分別為Xi和Yj，種群規模分別為S1和S2.其中:i=1,2,…,S1；j=1,2,…,S2.由于外層染色體由0-1變量構成，因此外層遺傳算法采用二進制編碼.為方便內層編碼，本文將運行時刻表中的到發時刻轉化為上午06:00:00至該時刻的間隔秒數，例如3 600即代表07:00:00這一時刻.由于內層染色體由正整數構成，因此內層遺傳算法采用實數編碼.外內層染色體結構見圖3.

圖3 外內層染色體結構

假設列車I在第Q站發生初始延誤.對于外層種群的初始化，本文首先將染色體中第Q個及之前的基因全部設為0，隨后從第Q+1個基因開始將其隨機賦值為0或1，若違反跳停約束則令其為0.以此類推，直到形成符合跳停約束的個體Xi.循環上述操作S1次即形成初始種群X.

對于內層種群的初始化，首先分析跳停次數最大情況下以及站站停調整模式下各列車在各站的到達時刻，并將這兩組時刻作為育種邊界，以此生成染色體中代表到達時刻的基因，隨后根據外層個體Xi和約束條件(12)生成代表出發時刻的基因，從而形成完整個體Yj.循環上述操作S2次即形成初始種群Y.

3.2 適應度函數

染色體適應度越大，表示其性能越好.因此內層個體Yj的適應度函數設計為

(21)

式中：C為一個足夠大的正整數；nk(Xi,Yj)為基于外層個體Xi生成的個體Yj違反第k個運行約束的次數；p為懲罰因子且為正數.

外層個體Xi的適應度取內層最優個體Ybest對應函數值的倒數，即

Fit(Xi)=1/T(Xi,Ybest)

(22)

3.3 種群演變策略

4 算例分析

4.1 基礎數據

以某城市地鐵線路為例.設線路共有20站，列車最大載客人數Cmax=1 400，計劃追蹤間隔I0=180 s，最小發到間隔I1=80 s，最小追蹤間隔I2=120 s.假設某列車在第二站因突發事故產生初始延誤，導致其在該站的出發時刻由08:01:40延誤至08:11:40.根據延誤時間可確定受延誤影響列車數n=10.

當乘客的出行終到站被跳停時，由于在跳停站前一站下車的決策比在后一站下車所需額外花費的時間明顯更少，因此本文設λ1=0.8，λ2=0.2.由文獻[9]可知城軌列車起停附加時間均在15 s左右，因此本文設τ1=τ2=15 s.

只研究線路單向跳停方案，該線路08:00:00-09:00:00時段內的OD量,見表2.

表2 OD客流

設定的列車停站時間、計劃區間運行時間及最小區間運行時間分別如下(單位為s).

圖4 函數收斂曲線

4.2 結果分析

優化后的列車運行調整方案見圖5.

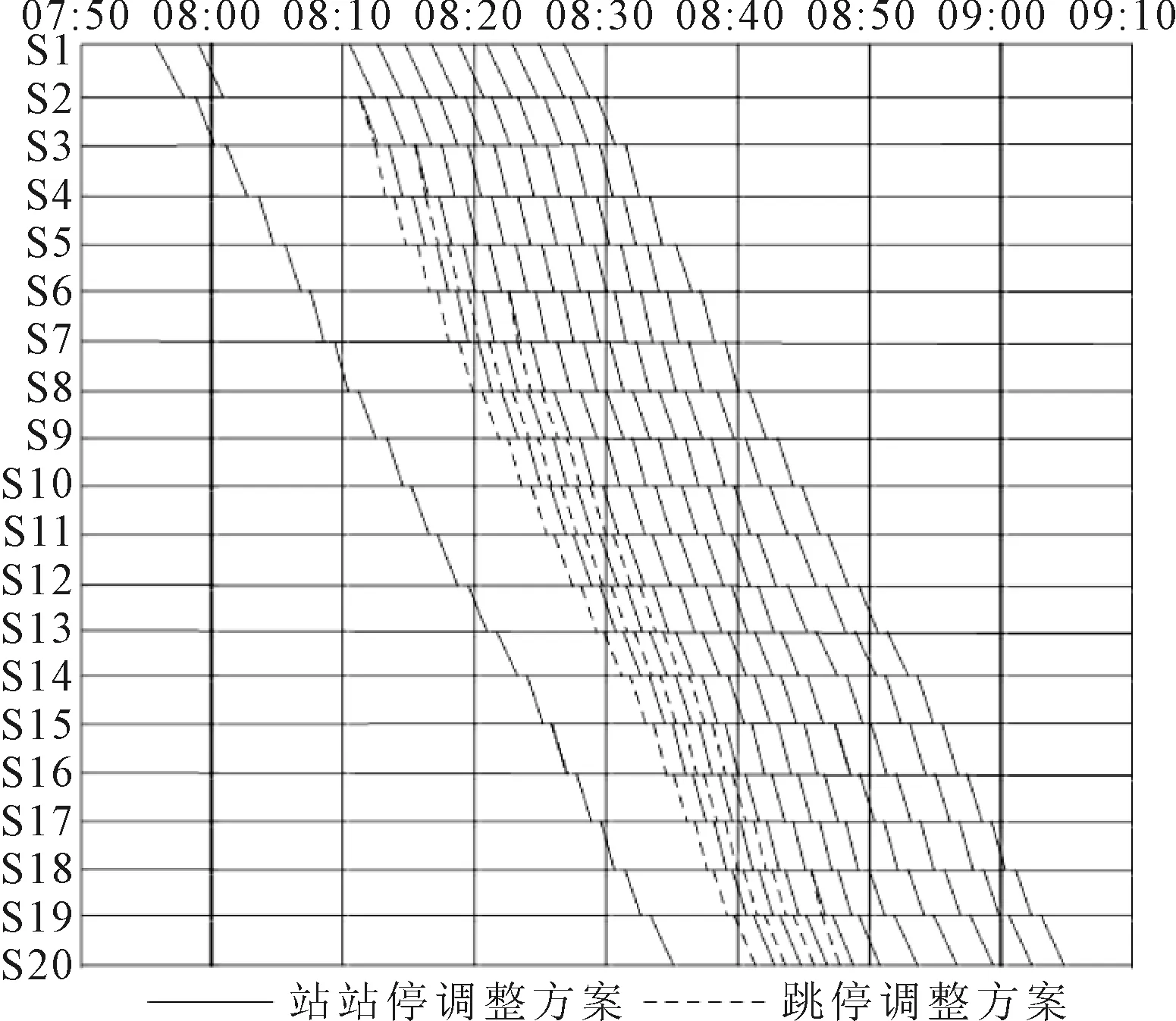
圖5 兩種調整方案下的列車運行圖

為驗證本模型的優化效果，將影響集合范圍內，計劃運行方案、站站停調整方案,以及跳停調整方案下的乘客總旅行時間、站臺乘客候車時間與乘客乘車時間一一進行對比(各時間的單位由s換為h，以方便目標值的比對)，跳停調整方案相對于站站停調整方案的優化效果見表3.

由于算例中列車存在延誤情況，且設定列車在恢復正點運行后均不再進行調整，因此跳停調整方案與站站停調整方案下得到的乘客總旅行時間必然大于計劃值.但由表3可知，在站臺乘客候車時間方面，模型求解得到的跳停調整方案相較于站站停調整方案，可以縮短6.6%因延誤而產生的額外站臺乘客候車時間；而在乘客乘車時間方面，模型求解得到的跳停調整方案和站站停調整方案相比于計劃運行方案均能夠有效縮減乘客的乘車時間，但跳停調整方案的縮減效果更加明顯.最后在整體層面上，結果表明本模型求解得到的跳停調整方案能夠顯著減少64.8%由列車延誤帶來的額外乘客總旅行時間.由此證明，在列車延誤條件下，建立的運行調整模型與算法在應對城軌列車運行調整問題上具有有效性及優越性.

表3 結果對比

5 結 束 語

文中從乘客的角度出發，分析列車跳停對乘客出行的影響，并結合城市軌道交通實際調度情況，考慮客流與列車運能之間的交互關系及列車延誤情況下列車跳停需考慮的約束，建立了以乘客總旅行時間為目標函數的運行調整優化模型，并根據模型特點設計了嵌套式遺傳算法來對模型進行求解.最后通過設計算例證明了本文模型及算法的有效性及優越性，可為城市軌道交通列車延誤條件下的實際調度提供理論支持.文中研究的前提之一是客流的到達為均勻分布，這與實際情況略有差別，因此動態客流下跳停方案的制定有待進一步深入研究.