S形曲線斜拉橋非線性靜風穩定性分析

楊吉新 劉 暢 黎建華 孫亭亭

(武漢理工大學交通學院1) 武漢 430063) (中國市政工程中南設計研究總院有限公司2) 武漢 430000)(中交第二航務工程勘察設計院有限公司3) 武漢 430060)

0 引 言

斜拉橋因其美觀的造型及較好的跨越能力在現代橋梁工程中的應用相當廣泛，但是大多數斜拉橋平面采用直線布置，當地形地貌復雜，橋墩位置受到限制等情況時，直線布置無法滿足設計需求，此時曲線布置成為了解決這一矛盾的方案之一[1].目前國內外曲線斜拉橋的設計及工程案例較為少見，國內外學者對于曲線斜拉橋的理論探討也不多.世界上首座S形曲線斜拉橋修建于日本首都高速公路Katoushika—Edogawa線上，橋梁全長455 m，橋型布置形式為四跨曲線連續箱梁及兩座主塔、密索結構[2].

大量的實驗表明:橋梁靜風失穩是造成橋梁傾覆結構破壞的主要原因之一.靜風失穩作為橋梁風荷載破壞中最危險的破壞形式之一，對比風載的其他作用，具有可預見性低、危害性大的特征[3].而具有特殊線形的斜拉橋由于結構受力的不同，其靜風失穩過程也與直線斜拉橋有一定差異，為了指導曲線斜拉橋抗風設計，保證其結構穩定性，研究曲線斜拉橋的靜風失穩無疑對豐富曲線斜拉橋的理論研究具有極其重要的意義[4].

1 工程背景

大連南部濱海大道西延伸線工程由主線工程和支線工程組成，主線工程起點為南部濱海大道星海灣跨海大橋西引橋登陸點，朝凌水灣項目規劃道路西行.支線工程以七賢東路和主線交匯處為起點，沿七賢東路向北，通過新建橋梁跨越黃浦路，并與學子街相連，繼續向北與紅綾路平交.本曲線斜拉橋建于南部濱海大道西延伸線工程(四標段)，位于遼寧省大連市高新園區，緊鄰小平島與大連軟件園區.主線斜拉橋平面為S形布置，采用雙塔單索面結構，跨徑為50 m+96 m+192 m+70 m=408 m.橋型布置圖見圖1.

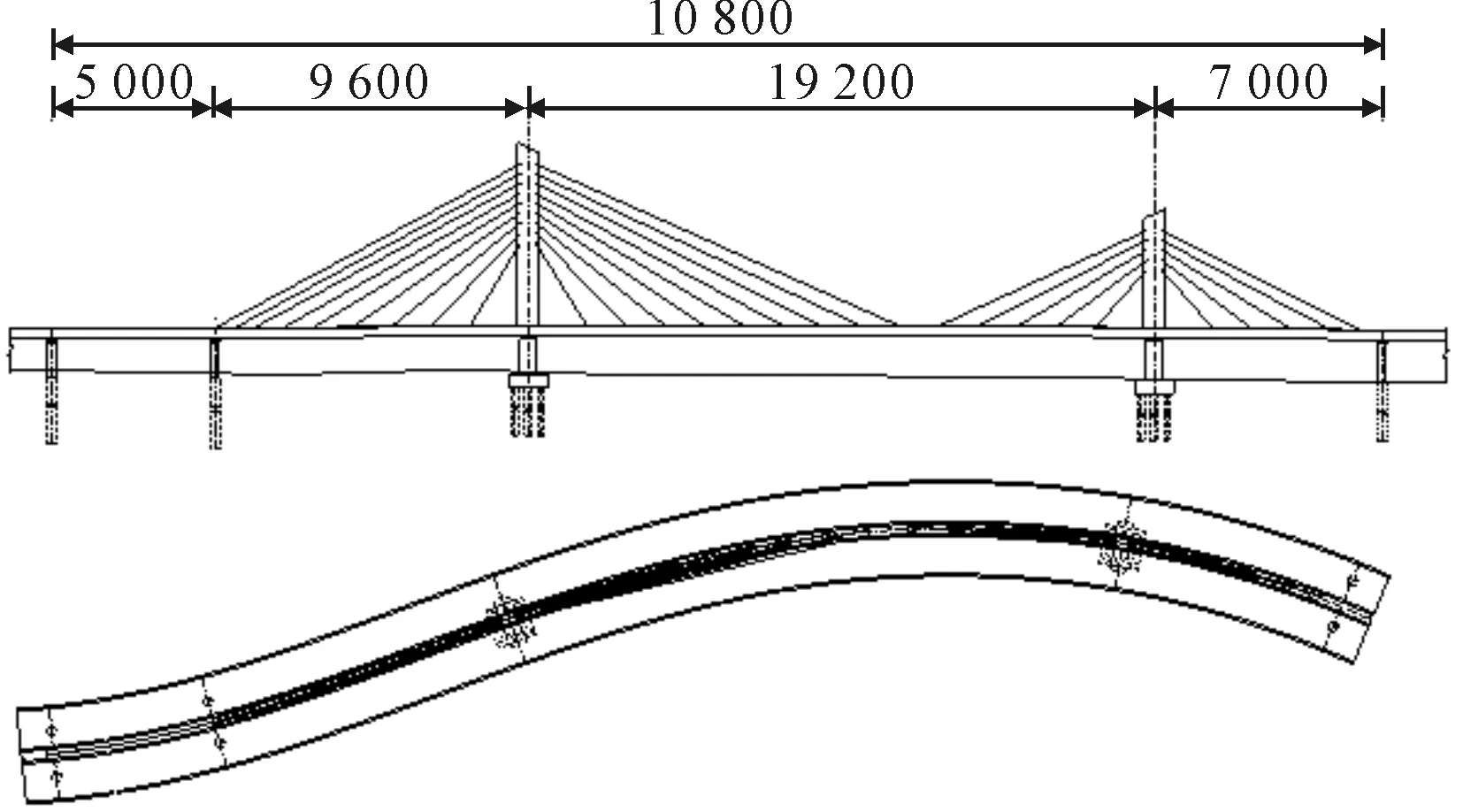
圖1 橋型布置圖

2 理論依據

風遇到障礙會導致流場發生改變，所以風在經過主梁時流場會重分布從而產生風壓對主梁施加風荷載[5].主梁在風載下產生變形，發生變形由于空間姿態的變化將對流場產生影響，又會繼續引發結構的扭轉變形，故斜拉橋的靜風失穩過程為非線性變化過程.對其模擬通常采用逐段增加風速進行迭代求解，求得結果.具體手段為通過擬定初始風速與風速增量計算主梁受到的靜風荷載，求得結構位移、扭轉角后進行內部迭代，內插求得三分力系數后疊加風速增量重新計算靜風荷載，進行外部迭代，最終判斷靜風失穩臨界風速[6].

斜拉橋的靜風失穩模型主要有二維模型和三維模型兩種.二維模型將橋梁扭轉失穩做了大量簡化，未考慮到實際情況中的彎扭耦合失穩的組合作用，尤其曲線斜拉橋由于其線型、結構受力的特殊性，單純將荷載和氣動常數的計算簡化為線性過程無法準確模擬工程實際[7].綜上，二維模型過于簡化了眾多影響因素會導致計算結果相對不精確甚至無法求解臨界風速，為更精確模擬研究曲線斜拉橋的抗風性能，采用更加符合實際簡化較少的非線性三維靜風失穩模型[8]，平衡方程為

K(δ)Δδ=ΔP(δ)

(1)

式中：K(δ)為結構的切線剛度矩陣，它可包含結構幾何剛度、線彈性剛度,以及塑性剛度矩陣；Δδ,ΔP(δ)分別為結構位移增量及風荷載增量向量，迭代的過程中要不斷的修正δ以滿足范數的要求.

3 靜三分力系數求解

研究橋梁抗風性能，靜三分力系數是及其重要的研究指標，采用常規解析法求解時由于主梁橫斷面的不同，自然風變化無常等特性不易求出準確解.因此，大多數工程實際中對橋梁結構的三分力系數進行求解一般采用規范要求的風洞試驗[9].風洞試驗準備工作及操作周期較為漫長，同時試驗費用需求較大，故在不具備風洞試驗條件的情況下，采用數值模擬的計算流體力學(CFD)法求解靜三分力系數成為首選[10].為檢驗數值模擬方法的正確性，選取大連理工大學實驗室中某類流線型主梁斷面風洞試驗作為樣本數據[11]，對比試驗數據與數值模型計算值見圖2.由圖2可知，模擬值的誤差均在10%以內.通過CFD法求得的計算值與風洞試驗數據相差無幾，說明數值模擬手段對計算主梁三分力系數具有較高的精度.

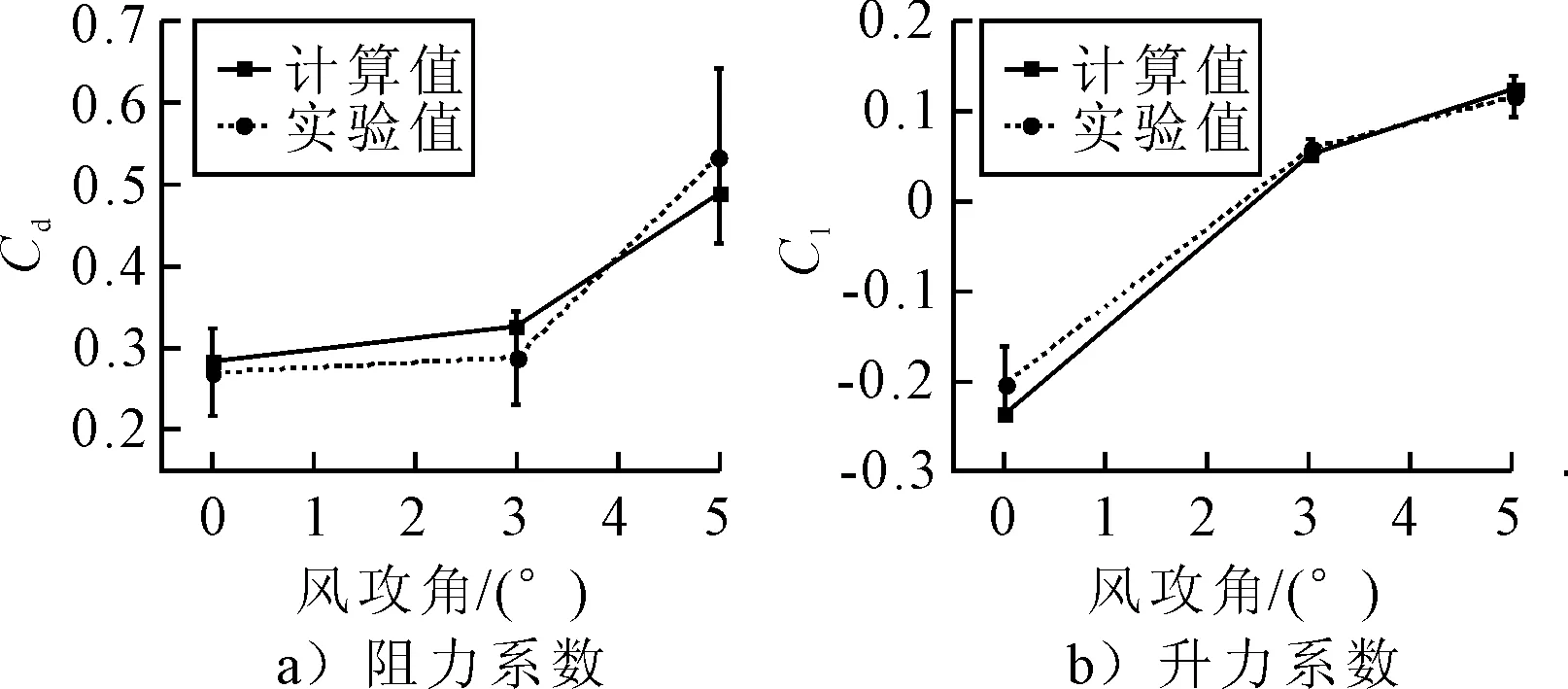
圖2 阻力和升力系數計算與試驗對比圖

采用WORKBENCH建立數值計算模型并采用ICEM網格劃分模塊對已建立模型劃分網格，主梁周圍采用O-block進行網格劃分[12]，主梁邊界層網格采用拋物線式加密，最接近邊界層的網格最小尺寸為1×10-4m.模型計算域入口邊界距離主梁為1.5倍主梁寬，上下邊界距離主梁距離均為1.5倍主梁寬，出口邊界距離主梁3倍主梁寬.通過旋轉主梁一定角度來模擬各類風攻角，模型全局網格劃分以及局部網格見圖3.

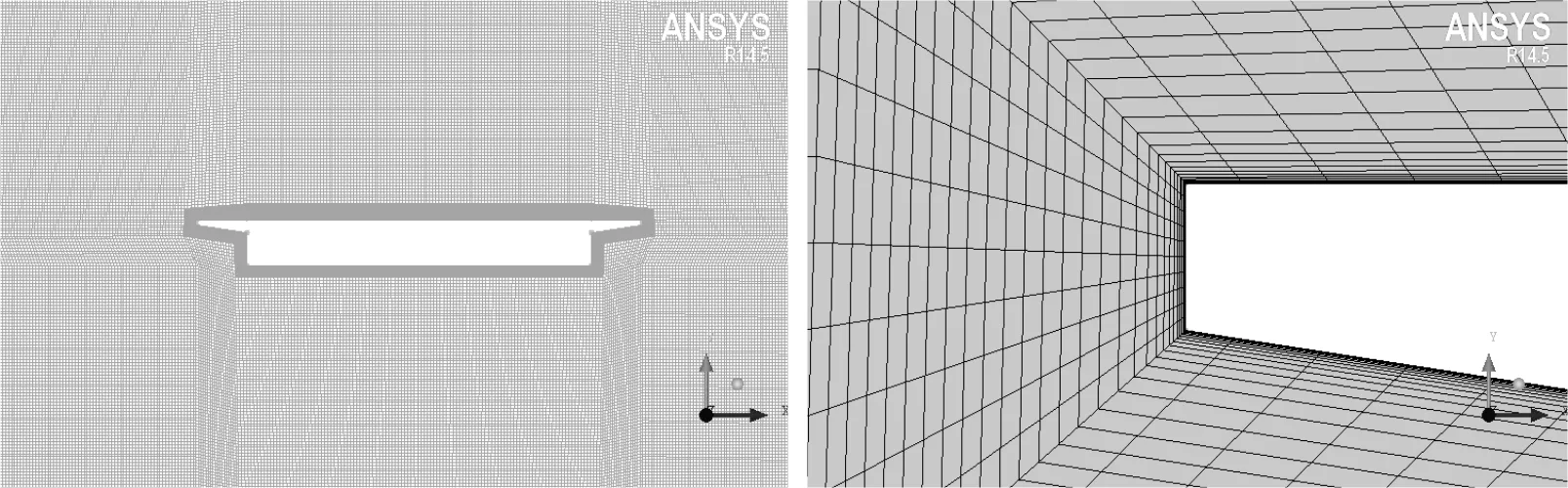
圖3 模型網格劃分

在FLUENT中分別對主梁斷面在-5°,-3°,0°+3°,+5°五類風攻角作用的數值模型進行計算[13]，選取風場的入口邊界平均風速為10 m/s，上下邊界采用對稱邊界模擬，出口定義為自由流動，計算過程中對靜三分力系數實時監控，計算并繪制不同風攻角作用下模型風速以及壓力云圖見圖4～5.

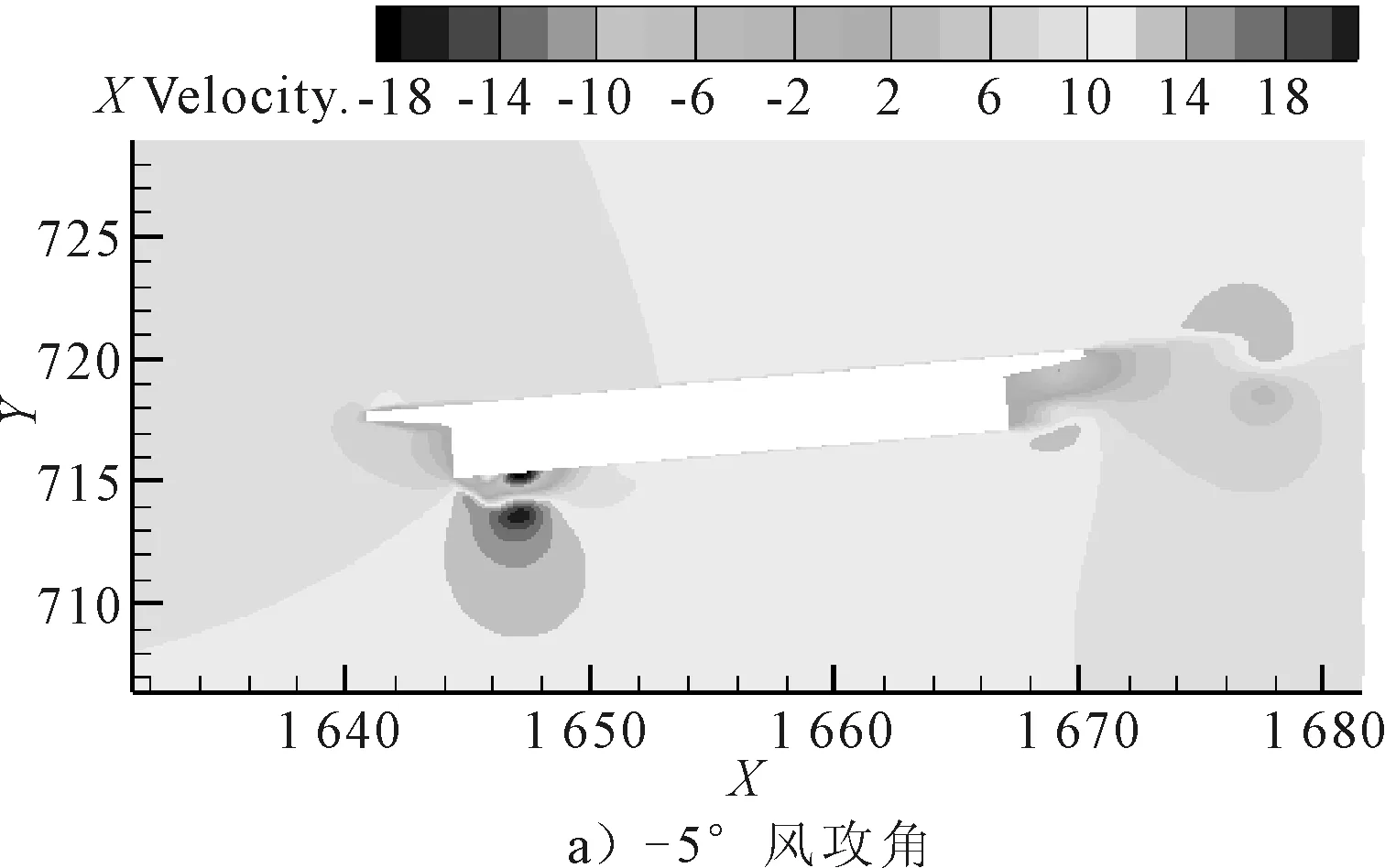
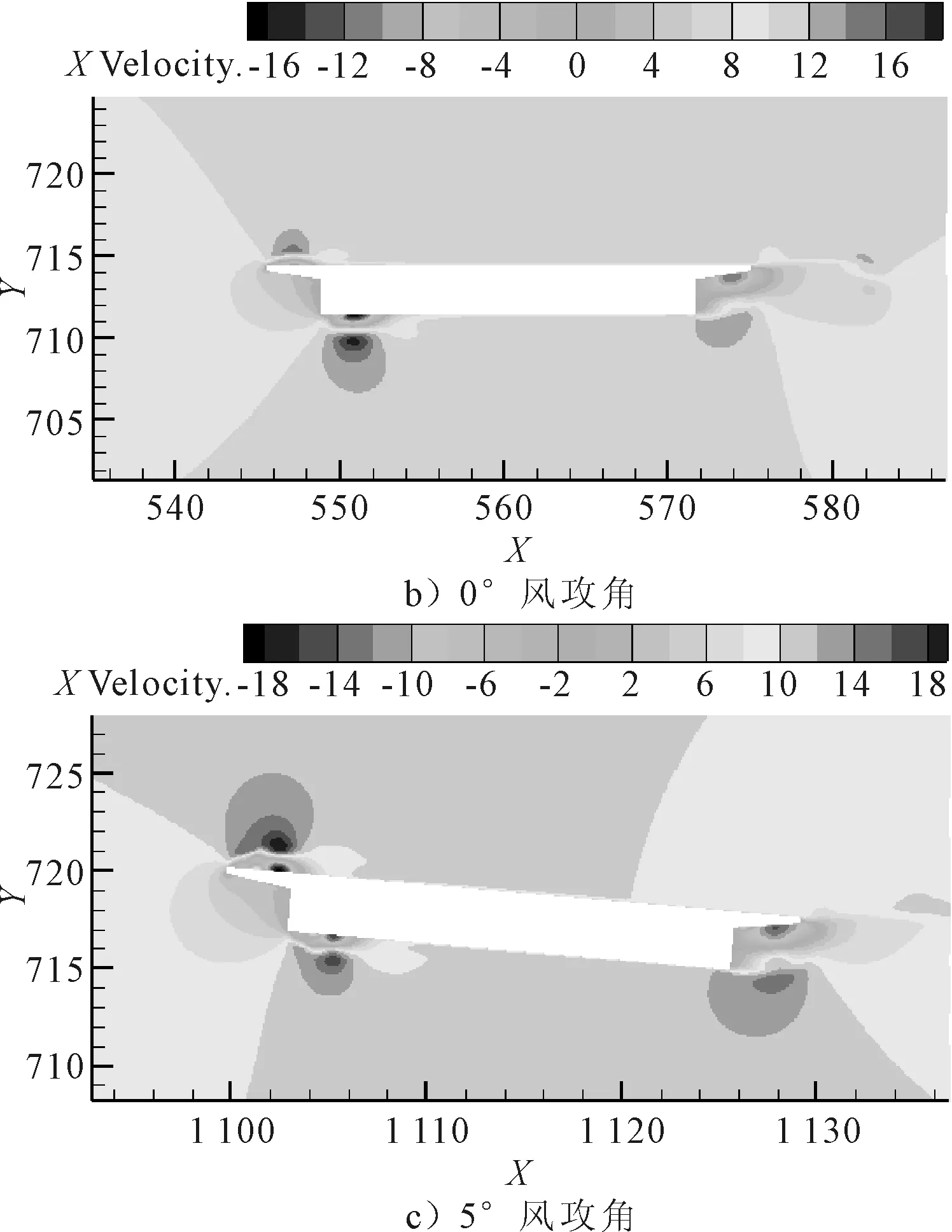
圖4 -5°,0°,5°風攻角模型風速云圖

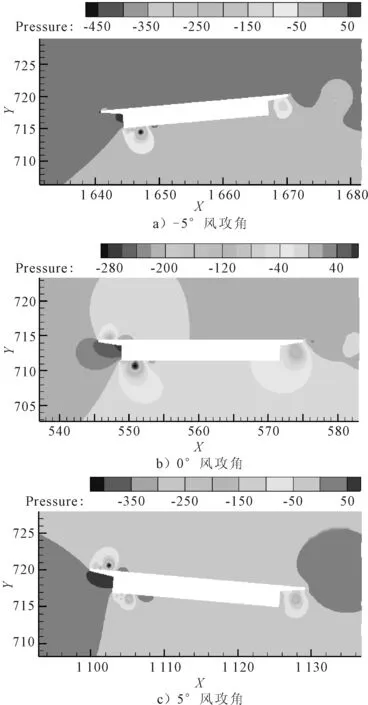
圖5 -5°,0°,5°風攻角模型壓力云圖

由圖4～5可知，風攻角的變化導致主梁周圍風速、風壓發生改變，風攻角為±5°時，主梁周圍的風速、風壓達到最大.隨著風攻角的增加，主梁周圍流場發生改變，風速在斷面端點處改變方向導致風速增大，風壓重新分布，主梁受到的阻力增大.同時風壓集中在主梁迎風側，風攻角為-5°時，主梁下端呈現負壓，風攻角逐漸增大，下端負壓區域面積減小，上端由正壓變為負壓，主梁受到的升力和扭矩增大.因此,風攻角的增加會增加橋梁風載，尤其對于曲線橋梁，自身受索力作用影響，抗扭能力較弱，風攻角的增加會使得曲線梁橋更易出現失穩.

繪制主梁橫斷面靜三分力系數變化圖見圖6，可以看出風攻角為-5°時Cl,Cm值即升力系數與扭矩系數均最小.隨著風攻角從-5°～+5°增加，兩者逐漸增大.當風攻角為0°時Cd值即阻力系數最小，隨著風攻角絕對值的增加，主梁迎風面積加大，阻力系數值隨之增大.

圖6 主梁靜三分力系數

為了分析不同風攻角情況下主梁周圍的壓力分布變化，對主梁節點進行編號[14]，指定主梁迎風側下表面端點為起始點，逆時針沿主梁輪廓線依次對主梁節點編號，根據數值模型中提取的不同風攻角作用下主梁各周向節點壓力值繪制折線圖,見圖7.

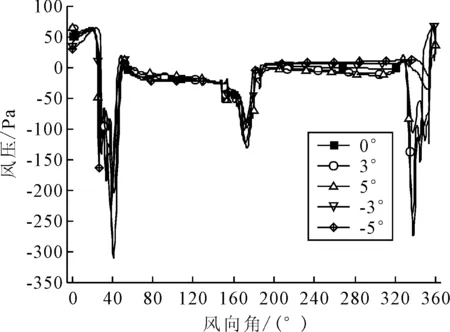
圖7 5類風攻角作用下主梁周向節點風壓圖

由圖7可知，隨著風攻角的增加，圖中兩側數據值即主梁迎風側的節點風壓變化均逐漸增大，中間數據及主梁背風測風壓波動較小.迎風側主梁上表面負壓值出現較大值，導致主梁轉矩大幅度增加.曲線斜拉橋在風攻角為±5°時迎風側主梁負壓出現極大波動，梁體會出現較明顯的扭轉.

4 曲線斜拉橋靜風失穩分析

在ANSYS中建立曲線斜拉橋有限元模型并劃分網格見圖8.

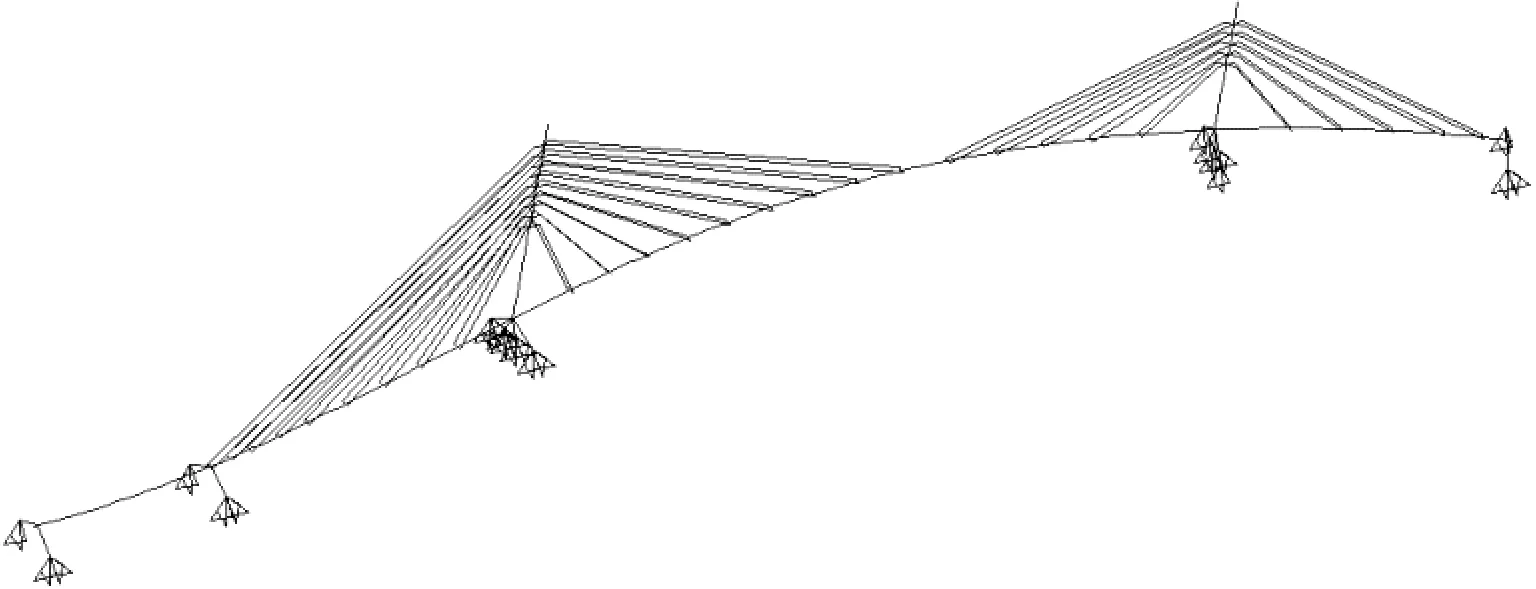
圖8 全橋有限元模型

將計算求得的靜三分力系數編輯為數據文件，采用ANSYS中程序設計語言編程，設置自重作用下為初始狀態，求解全橋的靜風穩定性[15-17].通過風速增量逐級迭代求解非線性靜風失穩臨界風速，風速臨界點為迭代開始發散時.通過數據分析求得當風速疊加到226 m/s時程序內部迭代開始發散，故該曲線斜拉橋的失穩臨界風速值為226 m/s.選擇主跨跨中節點，繪制其豎向變形增量迭代曲線以及扭轉角增量迭代曲線見圖9.

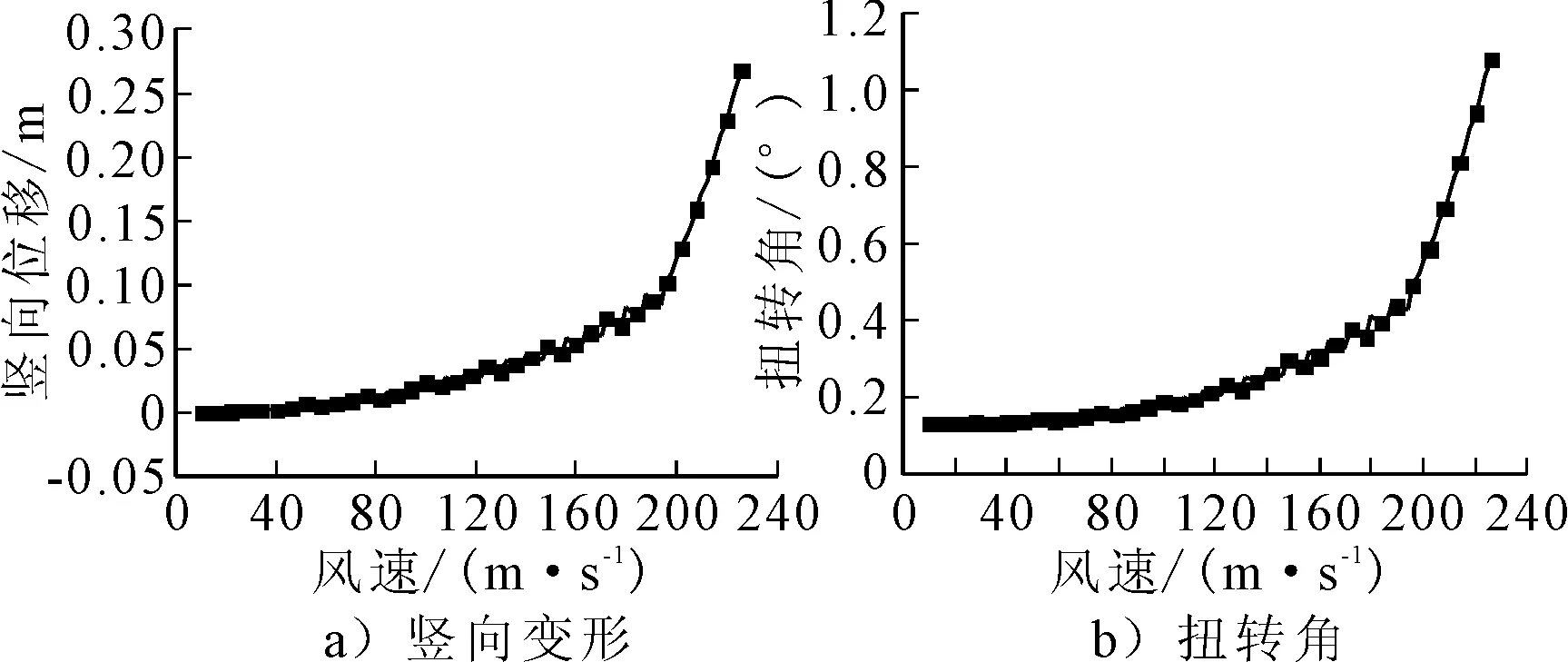
圖9 主跨跨中處節點豎向變形和扭轉角

由圖9可知，橋梁結構的豎向位移、扭轉角度呈現非線性變化，曲線斜拉橋跨中豎向位移、扭轉角前期變化幅度不大，當風速達到180 m/s時變形出現極速增長，在靜風失穩臨界值226 m/s附近，位移、扭轉變形開始發散，說明此時結構已經失穩，圖中展示的豎向位移、扭轉角的大幅度增加，表明結構失穩形態呈現為彎扭耦合變形失穩.整個失穩過程中，風速逐級增加風攻角不斷變化，導致結構的空間狀態不斷發生變化，每次變化后的橋梁風攻角不止包含起始風攻角，需加上結構變形產生的扭轉角.計算結果表明，角度、空間狀態的不斷變化導致結構的靜三分力系數發生變化，從而結構所受靜風荷載隨靜三分力系數改變而改變，主梁整體變形不遵從線性變化規律，如上圖所示呈現非線性變化.曲線斜拉橋由于空間結構的復雜性，橋梁會出現較大的扭轉變形，對風荷載的作用比較敏感，相比于直線斜拉橋，扭轉變形更大.

5 結 論

1) 風攻角的變化導致主梁周圍風速、風壓發生改變，風攻角為±5°時，主梁周圍的風速、風壓達到最大.風壓集中在主梁迎風側，風攻角為-5°時，主梁下端呈現負壓，風攻角逐漸增大，下端負壓區域面積減小，上端由正壓變為負壓，主梁受到的升力和扭矩增大.因此風攻角的增加會增加橋梁風載，尤其對于曲線橋梁，自身受索力作用影響，抗扭能力較弱，風攻角的增加會使得曲線梁橋更易出現失穩.

2) 隨著風攻角的增加，升力系數與轉矩系數呈現增長趨勢；阻力系數在風攻角為0°時最小，隨著風攻角絕對值的增加，主梁迎風面積加大，阻力系數值隨之增大.

3) 隨著風攻角的增加，迎風側主梁風壓變化均逐漸增大，中間數據值以及背風側主梁風壓波動較小.迎風側主梁上表面負壓值出現較大值，導致主梁扭矩大幅度增加.曲線斜拉橋在風攻角較大時迎風側主梁負壓出現極大波動，梁體會出現較明顯的扭轉現象.

4) 曲線斜拉橋跨中位移在豎向上前期變化幅度不大，扭轉角度變化平穩.當風速超過180 m/s后出現極速增加，在臨界值226 m/s附近結構已經失穩，且失穩形態呈現為彎扭耦合式.曲線斜拉橋由于空間結構的復雜性，橋梁會出現較大的扭轉變形，對風荷載的作用比較敏感，相比于直線斜拉橋，扭轉變形更大.