變限積分函數求導數的方法

侯玉雙，何莉敏

侯玉雙，何莉敏

（內蒙古科技大學 理學院，內蒙古 包頭 014010）

變限積分函數；導數；牛頓-萊布尼茲公式；原函數；被積函數

1　求解變限積分函數導數時的常見錯誤

在高等數學教學中，變限積分函數求導數是學生必修且必考的重要知識點之一，也是教學的難點之一.關于它的講授幾乎所有高等數學教材[1-7]都是以定理形式呈現．

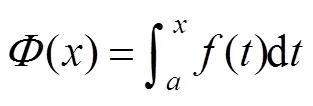
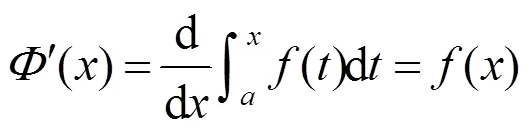
關于該定理的證明，運用的是導數的定義．講完該定理及其證明后學生自然記住了公式（2），但很多學生在利用其求變限積分函數的導數時，不能正確使用該定理，做題時經常出現下列3種錯誤情況：

這3種錯誤，在初學者學習變限積分函數求導數時常見且難以避免，即使對求對的多數初學者而言，也是因為在考前反復僵硬地記住了3個公式

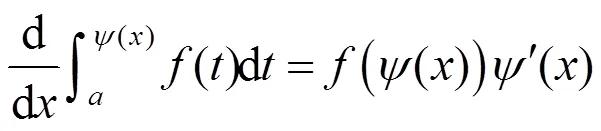
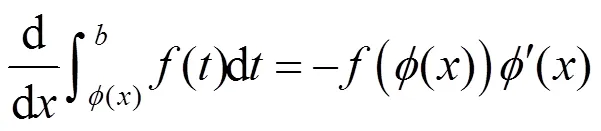
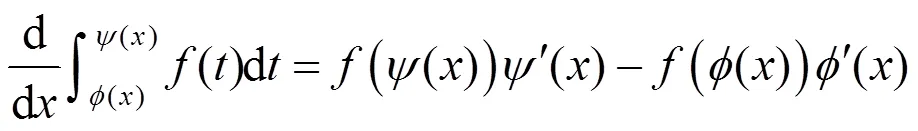
2　求解變限積分函數導數的方法

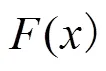
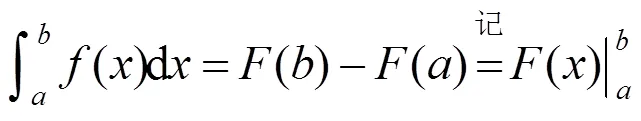
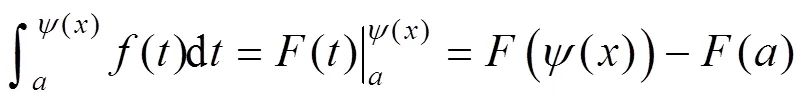
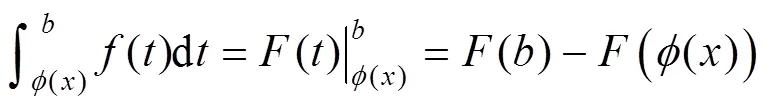
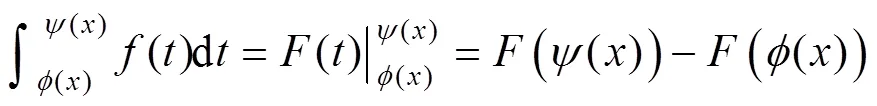
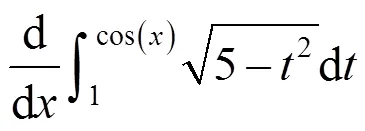
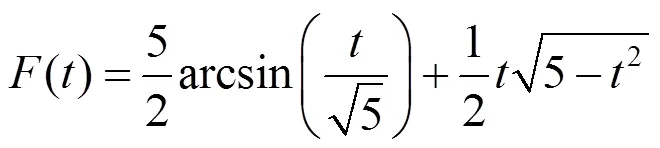
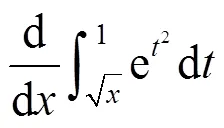
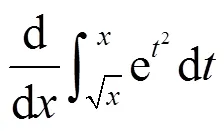
[1] 同濟大學數學教研室．高等數學（上冊）[M]．7版．北京：高等教育出版社，2019：238-250

[2] 王嘉謀，石琳．高等數學（上冊）[M]．北京：高等教育出版社，2011：241-244

[3] 華東師范大學數學系．數學分析（上冊）[M]．4版．北京：高等教育出版社，2010：95-97

[4] 歐陽光，朱學炎，金福林，等．數學分析（上冊）[M]．3版．北京：高等教育出版社，2007：122-128

[5] 四川大學數學系．高等數學[M]．3版．北京：高等教育出版社，1995：313-314

[6] 孫弘安．高等數學[M]．北京：北京師范大學出版社，2000：198-201

[7] 中華人民共和國教育部考試中心．2004年全國碩士研究生入學統一考試數學考試參考書[M]．北京：高等教育出版社，2003：195-198

[8] 宋傳靜．高等數學教學中變限積分函數求導公式的應用[J]．河南教育學院學報：自然科學版，2019，28（3）：54-58

[9] 呂紀榮，王士虎．關于變限積分函數求導問題的研究與應用[J]．數學學習與研究，2015（19）：134-135，137

[10] 于風宏．高等數學教學中變限積分函數的求導方法[J]．數學學習與研究，2014（19）：75

HOU Yushuang，HE Limin

（School of Science，Inner Mongolia University of Science and Technology，Baotou 014010，China）

variable limit integral function；derivative；Newton-Leibniz formula；original function；integrand function

O173∶G642.0

A

10.3969/j.issn.1007-9831.2020.09.011

1007-9831（2020）09-0046-04

2020-04-14

內蒙古自治區自然科學基金項目（2019MS06022）

侯玉雙（1979-）， 女，河北遵化人，副教授，博士，從事非線性動力學系統及高等數學教學研究．E-mail：764998599@qq.com