薛定諤方程的一種新教學思路
姚林紅,李慧生
薛定諤方程的一種新教學思路
姚林紅,李慧生
(中北大學 理學院,山西 太原 030051)
在理解微觀粒子波粒二像性特征的基礎上,對比實數軸和復平面的不同,猜出自由粒子波函數的數學形式.這種結合物理圖像探索數學形式的教學方法,不僅有助于學生理解并接受薛定諤方程,而且能夠給學生帶來啟發,有助于學生科研能力和創新能力的培養.
波粒二像性;薛定諤方程;波函數;科研能力;創新能力
薛定諤方程是量子力學中最重要、最基本的定理,也是大學物理量子部分的教學重點和難點.但是由于日常生活中很難接觸到需要用量子力學來解決的實際問題,因此學生的生活經驗多局限于經典物理的情況,對于量子力學尤其是薛定諤方程,學生理解并接受起來顯得十分困難.甚至直到現在量子力學的一些問題仍然懸而未決[1].如何才能將薛定諤方程這部分內容講解得深入淺出,讓學生更好地理解和接受薛定諤方程一直是物理教學工作者思考的問題[2-5].
1 薛定諤方程教學的一般思路
在大部分的大學物理教材和量子力學教材中,薛定諤方程都是在對比平面簡諧波[6]
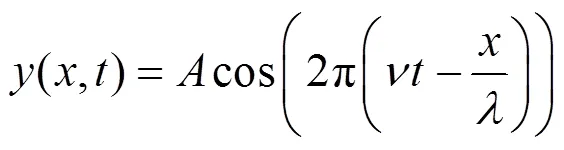
形式的基礎上,結合德波羅意關系式[7]
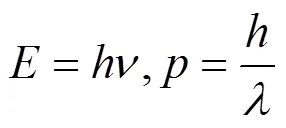
猜測微觀自由粒子的波函數應該用
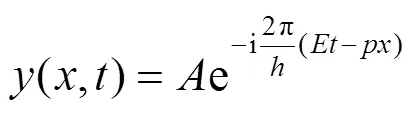
表示,在此基礎上利用數學工具逐步猜測出薛定諤方程的形式.
但是從平面簡諧波實數形式的波函數(1),到自由粒子的復數形式的波函數(3)這樣的跨域顯得非常突兀,導致學生對薛定諤方程理解和接受起來特別的困難.
2 從微觀粒子波粒二象性特征出發猜出薛定諤方程的教學思路
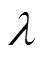
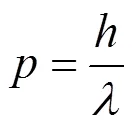
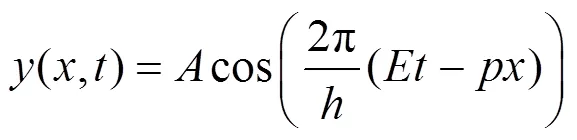
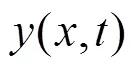
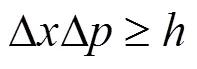
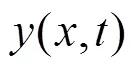
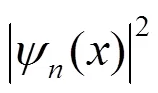
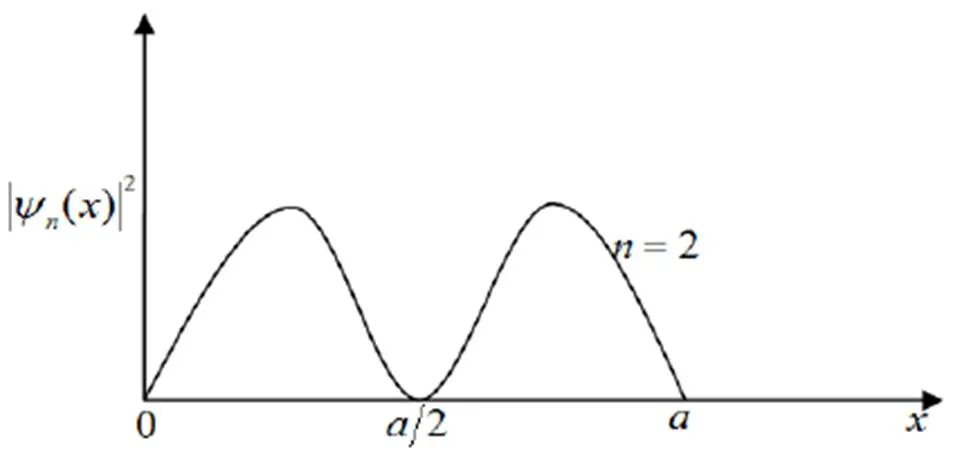
圖1 一維無限深勢阱中電子的概率分布
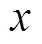

圖2 粒子離開原點的距離
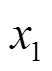
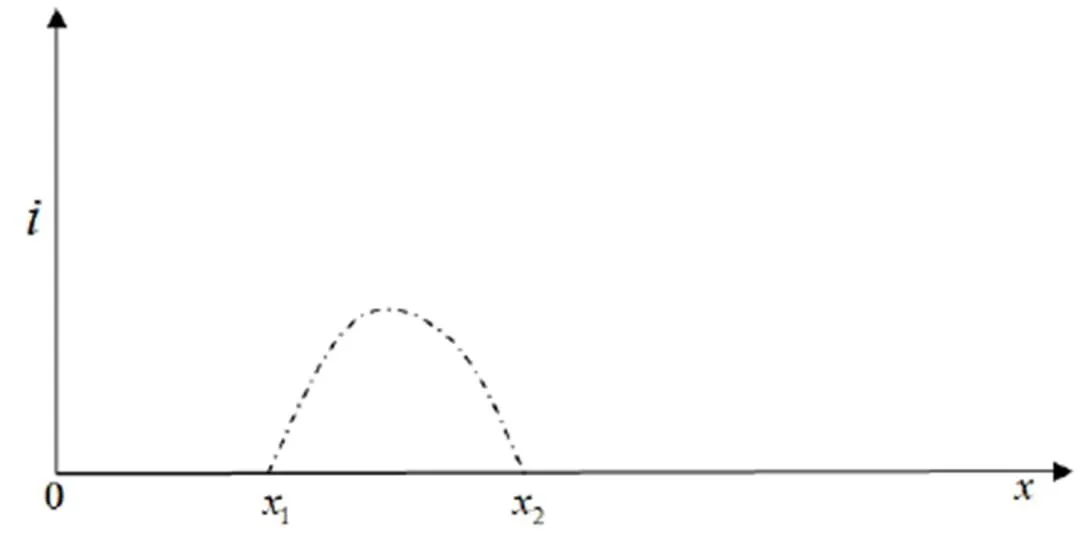
圖3 粒子經復平面從一個點到達另一個點
既然通過從實數軸擴展到復平面可以解決粒子運動斷續的問題,那么受到這個問題的啟發,微觀粒子的波函數也相應在實函數式(4)的形式上加以修正為復函數式(3).方程(3)與(4)雖然都具有波動性,但是方程(3)表示的是與復平面對應的點,而方程(4)則表示的是與實數軸上對應的點.當然,這種猜測未必正確,但是通過這樣的類比和思考,復函數式(3)的猜出就顯得比較自然,而直接假設與平面簡諧波對應的微觀粒子的波函數則顯得非常的突兀,對初學者特別難以理解和接受.
在猜出與平面簡諧波對應的微觀粒子的波動方程是式(3)之后,接下來再按照一般的講解思路,運用數學的方法逐漸猜測出描述微觀粒子的薛定諤方程,這樣學生理解和接受起薛定諤方程來就比較容易了.隨后在探討波函數的物理意義時,再引入波恩的概率波解釋,強調有物理意義的是波函數的模方,函數的模方代表了粒子出現在空間的概率密度[8]341.這樣復數式(3)形式到底表示什么就不再是困擾學生的問題了.
3 結語
薛定諤方程是大學物理量子部分的教學重點和難點,但是理解并接受薛定諤方程十分困難.在深刻理解微觀粒子波粒二像性特征的基礎上,對比實數軸和復平面的不同,并借鑒機械波和電磁波的數學形式猜出自由粒子波函數式(3)的形式,彌補了薛定諤方程這部分內容一般教學方法的不足.這種從探索物理圖像再到猜出數學形式物理定律的教學方法,不僅有助于學生理解薛定諤方程,而且能夠給學生帶來啟發,有助于學生科研能力和創新能力的培養.
[1] 郭光燦.量子十問之四“薛定諤貓”為什么會自然死亡?[J].物理,2019,48(1):37-38
[2 張立彬,涂成厚.中外量子力學教材經典知識點的區別與思考[J].大學物理,2013,32(4):38-40
[3] 李愛君,周戰榮,朱海飛.大學物理課程中“波函數薛定諤方程”的教學探討[J].物理與工程,2018,28(4):78-87
[4] 向梅,馬曉東,路俊哲,等.關于量子力學中波函數復數表示的討論[J].大學物理,2017,36(11):32-34
[5] 魏標,廖榮寶,金鳳,等.淺議共軛薛定諤方程及其物理量算符[J].阜陽師范學院學報:自然科學版,2019,36(1):10-12
[6] 許麗萍,魏天杰.物理學原理簡明教程(下冊)[M].北京:高等教育出版社,2013:214
[7] 周世勛.量子力學教程[M].北京:高等教育出版社,2006:12
[8] 馬文蔚,周雨青,解希順.物理學(下冊)[M].5版.北京:高等教育出版社,2014:338,341
[9] 李金海,方恒忠,李子良.氫原子電子云密度分布分析[J].大學物理,2004,23(3):13-17
A new teaching method of Schrodinger equation
YAO Linhong,LI Huisheng
(School of Science,North University of China,Taiyuan 030051,China)
On the basis of understanding the characteristics of particle wave-particle duality,by comparing the difference between real number line and complex plane,and finally guesses the mathematical form of free particle wave function.This teaching method,which combines physical images to explore mathematical forms,not only helps students to understand and accept the Schrodinger equation,but also brings inspiration to students,which is conducive to the cultivation of students′ scientific research ability and innovation ability.
wave-particle duality;Schrodinger equation;wave function;scientific research ability;innovation ability
O302∶G642.0
A
10.3969/j.issn.1007-9831.2020.09.018
1007-9831(2020)09-0071-04
2020-04-07
山西省自然基金面上項目(201801D121027)
姚林紅(1982-),女,山西太原人,講師,碩士,從事數學物理研究.E-mail:yaolinhong5@126.com

