運用“畫說”策略 培養數學“四能”
——以北師大版六年級《圓的面積（二）》教學為例

林英語

（晉江市實驗小學，福建 晉江36220）

《義務教育數學課程標準（2011 年版）》將發現與提出問題、分析與解決問題作為“四能”列入數學課程總目標，［1］由此帶動數學“四能”培養的教學實踐改革。在一系列教學實踐改革中，教學者不斷嘗試與融入各種有創意的課堂教學策略，如“玩數學”“做數學”“演數學”等等，期望以多元化的策略促進學生數學“四能”的發展，突破“聽數學”“算數學”等傳統教學策略在能力培養上的局限。以北師大版六年級《圓的面積（二）》一課為例，分析“畫數學”“說數學”策略在數學“四能”培養上的作用與運用。

一、以“畫”助“說”，驅動問題提出

數學學習的過程實質是一個問題提出與問題解決相互關聯、互為促動的迭代活動。結合數學“四能”來看，可將發現與提出問題統整為問題提出，將分析與解決問題歸屬于問題解決。在問題提出的活動中，發現問題側重于對問題的關注與對問題的敏感度，體現為學生能多角度、多方面從看似無關的現象中敏感地發現問題的存在；提出問題則是對問題“目標、給定與差距”等要素的再思考，對問題的數學化表達與精致，并包含對問題價值性、適合性、可探究性的評價與選定。能否提出具有思考性、探究性和價值性的數學問題，在一定程度上受限于問題提出情境的刺激。而數學問題提出的情境多種多樣，但一般認為可歸為現實情境、數學情境、科學情境［2］三種類型。因此，從情境與問題的關系看，數學問題提出就是引導學生在不同語言形式表達的情境中閱讀、發現、提取數學信息，并從目標、給定、差距等方向去分析信息間的聯結，以數學化的形式將已知與欲知信息問題化。在眾多的情境表達方式中，由于圖形語言可以把復雜的信息簡明化、形象化，并對應于幾何直觀與空間想象，因此，在情境中運用畫圖策略，以圖形來描述信息或分析信息，有利于學生運用數學直觀、空間想象說出信息關聯，發現數學關系，進而驅動數學問題提出。

例如，在《圓的面積（二）》一課的問題提出階段，在前課《圓的面積（一）》已經知道圓可轉變為平行四邊形進行面積推導的基礎上，教師可呈現圓的圖形、公式與平行四邊形的公式。然后運用“畫圖”策略，畫出平行四邊形的一條對角線，引導學生在畫中看、看中思、思中問，用幾何直觀、空間想象、數學直覺、邏輯推理、聯想等思維，發現、提取與分析信息，建立起圓、平行四邊形、三角形等圖形與公式的思維聯結，提出“圓可否轉化為三角形，并用三角形的面積來推導圓的面積”的探索性問題。通過比較分析前課所知的圓面積公式與三角形面積公式，推測三角形的底是圓的周長、高是圓的半徑（如圖1），使問題進一步數學化。這樣的教學設計體現了圖形語言在情境中驅動問題提出的作用。

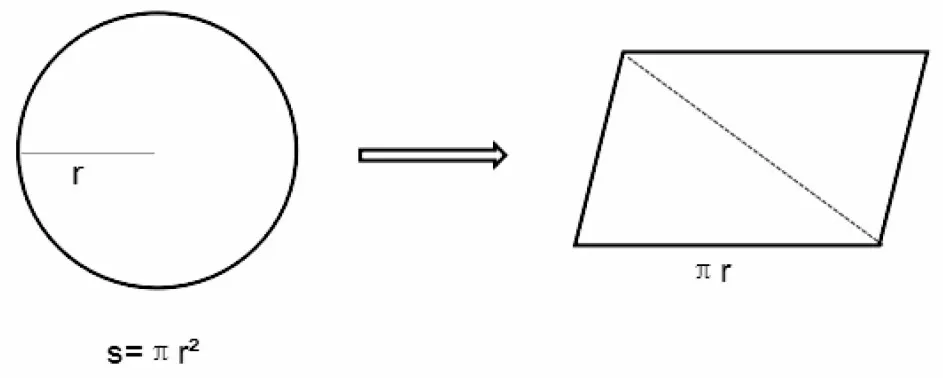
圖1

二、以“畫”導“說”，促進問題解決

問題提出后，學生的學習進程必然是分析問題與解決問題。分析與解決數學問題，實質上是數學思維、思路、思想的運用與發展。面對新的問題，學生會如何思考與分析呢？會運用哪些思想與思維呢？會采用哪種思路呢？探明這些問題，是推進學習進程、培養問題解決能力的關鍵。這些問題具有內隱的特點，需要教師采用有效策略將其外顯化，以更好地觀察與評估。“畫形”“說理”是較好的思維外顯化形式，一種以“畫形”將思維可視化，另一種則以“說理”將思維可聽化。將“畫形”“說理”交融運用于問題分析與解決的過程中，一方面能增強學生運用數形結合思想、數學直觀、空間想象于分析問題的意識與能力；另一方面能以“畫”導“說”，以形（形象思維）通理（抽象思維），促進問題解決。同時，教師通過觀察與分析學生“畫形”“說理”的角度、方式與內容，能更準確地發現與評價學生數學問題解決的思考方式、能力水平，從而增強學習性評價的精準性，使補充與調動學生數學活動經驗、引導學生運用數學觀念與調整思維思路能更加適時、適宜與適效，實現適性且深度的教學。

例如，在《圓的面積（二）》一課的問題解決階段，教師可讓學生小組合作，有序畫出圓形的環與三角形的線（如圖2），引導學生邊操作、邊觀察、邊思考，并在小組內說說兩個圖形的可能關聯，小組間交流與質疑想法。首先，通過操作性畫圖，使學生產生思維的基點；其次，通過比較、觀察，觸動學生思維的生長點；最后，通過生生間的互動“說”，促使思維延伸與拓展，形成大膽的理性的推測，體現以“畫”導“說”。為了使推測有理據可“說”，隨后的教學可結合剪圓杯墊重組成三角形的直觀操作活動找出證據，并在此基礎上引入數學詞匯或符號，說一說推導與發現，概括說出圓的面積可轉化為三角形的面積進行求導。

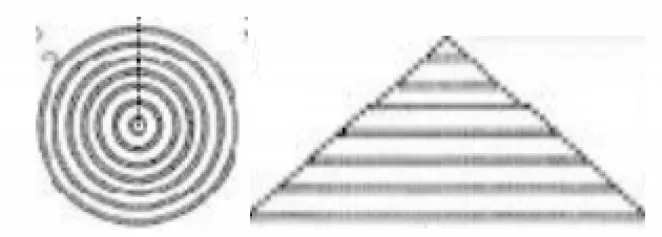
圖2

三、“畫”“說”結合，參悟問題本質

動作語言、文字語言、圖形語言、符號語言等均是數學問題提出與問題解決教學的表征形式。不同表征形式對應不同的思維類型，如動作語言、圖形語言對應動作直觀、幾何直觀，側重形象思維；文字語言、符號語言側重于抽象思維、邏輯思維等。通過綜合與靈活運用多種表征形式來展開數學問題提出與問題解決的教學，更有利于迎合不同學生的思維優勢，發展學生的綜合思維。對于發展“四能”，實現“三會”（會用數學眼光觀察世界，會用數學思維思考世界，會用數學語言表達世界）［3］也具有重要的意義。“畫”“說”兩種活動，或者兩種表達方式，基本上囊括了動作語言、文字語言、圖形語言、符號語言等多種語言形式，并且具有過程性與結果性的特點，能較好地落實教學評的協調一致與融通一體。在教學總結階段，將“畫”“說”有機結合呈現，有助于學生運用多種思維參悟數學問題本質，運用數學抽象總結數學思想與數學方法。

例如，在《圓的面積（二）》的總結階段，可運用學習單，呈現多種推導圓面積公式的圖形（如圖3）。通過問題清單，如“觀察這些圖形，你發現圓的面積是如何推導的？”“你能說說圓的面積推導運用了什么數學思想或方法嗎？”“這種數學思想或方法，你以前用過嗎？還可以運用在什么數學問題的解決上呢？”引導學生運用歸納推理，抽象概括，進行抽象“說”、概括“說”、本質“說”、遷移應用“說”，從而使教學指向致知（圓面積與半徑大小有關，與半徑平方成正比）、明理（等積變形思想）、達用（在生活生產實踐中，在新數學問題的解決中的思想與方法應用）的境界。

圖3