基于改進量子粒子群算法的火電廠再熱汽溫調節系統PID參數自整定

摘要:鑒于熱控工作人員的技術水平和經驗不足等問題,目前火電廠中許多控制回路整定效果不佳,因此PID參數的自整定具有極其重要的意義。為此,提出了一種基于改進量子粒子群算法的PID參數自整定方法,并采用MATLAB軟件對火電廠再熱汽溫調節系統進行了仿真及PID參數自整定。通過與工程上的臨界比例度法、傳統粒子群算法、傳統量子粒子群算法自整定的仿真結果相比較,證明了基于改進量子粒子群算法的PID參數自整定方法的優越性。
關鍵詞:改進量子粒子群算法;PID;參數自整定;再熱汽溫調節系統;仿真
0 引言
人為手動整定PID參數,不僅耗時費力,而且整定效果與人員的整定水平息息相關,更無法獲取令控制效果最佳的PID參數。因此,PID參數的自整定已成為國內外很多學者關注的焦點。目前已有不少PID參數整定的優化方法,比如蟻群算法、神經網絡、遺傳算法、粒子群算法等。粒子群算法(PSO)是典型的群體智能優化算法之一,具有參數較少、尋優能力強以及易于實現等優點[1]。但是該算法也具有一定局限性,因此國內外學者對傳統粒子群算法進行了不同程度的優化[2-4],Sun[5-6]等人結合物理量子理論,提出了量子粒子群算法(QPSO),但QPSO算法在后期迭代中存在陷入局部最優值的現象。
針對QPSO算法的缺點,本文通過引入擾動函數來更新粒子的物理位置,從而給予粒子擺脫局部最優的外部力量,克服粒子尋找質量停滯不前的問題,將粒子搜尋范圍擴大,最終跳出局部最優范圍,并將這種改進QPSO算法應用于火電廠再熱汽溫調節系統的PID參數自整定中,通過與工程上的臨界比例度法、傳統PSO算法、傳統QPSO算法自整定的仿真結果對比,證明本文提出的改進QPSO算法具有更優越的性能,使再熱汽溫調節系統獲得更好的調節質量。
1 引入擾動函數的改進QPSO算法
本文采用變異機制,引入擾動函數為QPSO算法提供一個外部力量,作為粒子擺脫局部最優的驅動力,改變粒子搜尋質量停滯不前的狀態,將粒子的搜索空間擴大,幫助粒子跳出早熟的局面,采用的擾動函數如下:
式中,gbestk為第k代第i個粒子的個體歷史最好位置適應度與群體歷史最好位置;e為變異步距;N(0,1)為均值為0、方差為1的高斯隨機分布,e越大,擾動越大,粒子跳出局部最優解的能力越強,但算法的收斂性能越弱,因此需要通過仿真選擇適當的變異步距。
與此同時,為了既保證算法的收斂性能,又保證算法的尋優能力,上述變異機制僅用于算法的中期。
2 改進QPSO算法,優化再熱汽溫調節系統的PID參數
2.1? ? 再熱汽溫對象動態特性
本文再熱汽溫控制系統PID參數優化和仿真所采用的模型如下[7]:
2.2? ? 臨界比例度法優化再熱汽溫調節系統PID參數
采用MATLAB軟件對臨界比例度法的PID整定進行仿真,得到該模型PID的各參數為:Kp=1.094,Ki=0.001 7,Kd=147.875,在此基礎上,進行階躍擾動試驗,仿真結果如圖1所示。
采用臨界比例度法,系統產生臨界振蕩的條件是系統的階數在3階及3階以上,否則易發生系統高頻振蕩,危及系統安全,因此在工程上實際應用臨界比例度法整定PID參數具有一定的危險性和局限性。
2.3? ? 傳統PSO算法優化再熱汽溫調節系統PID參數
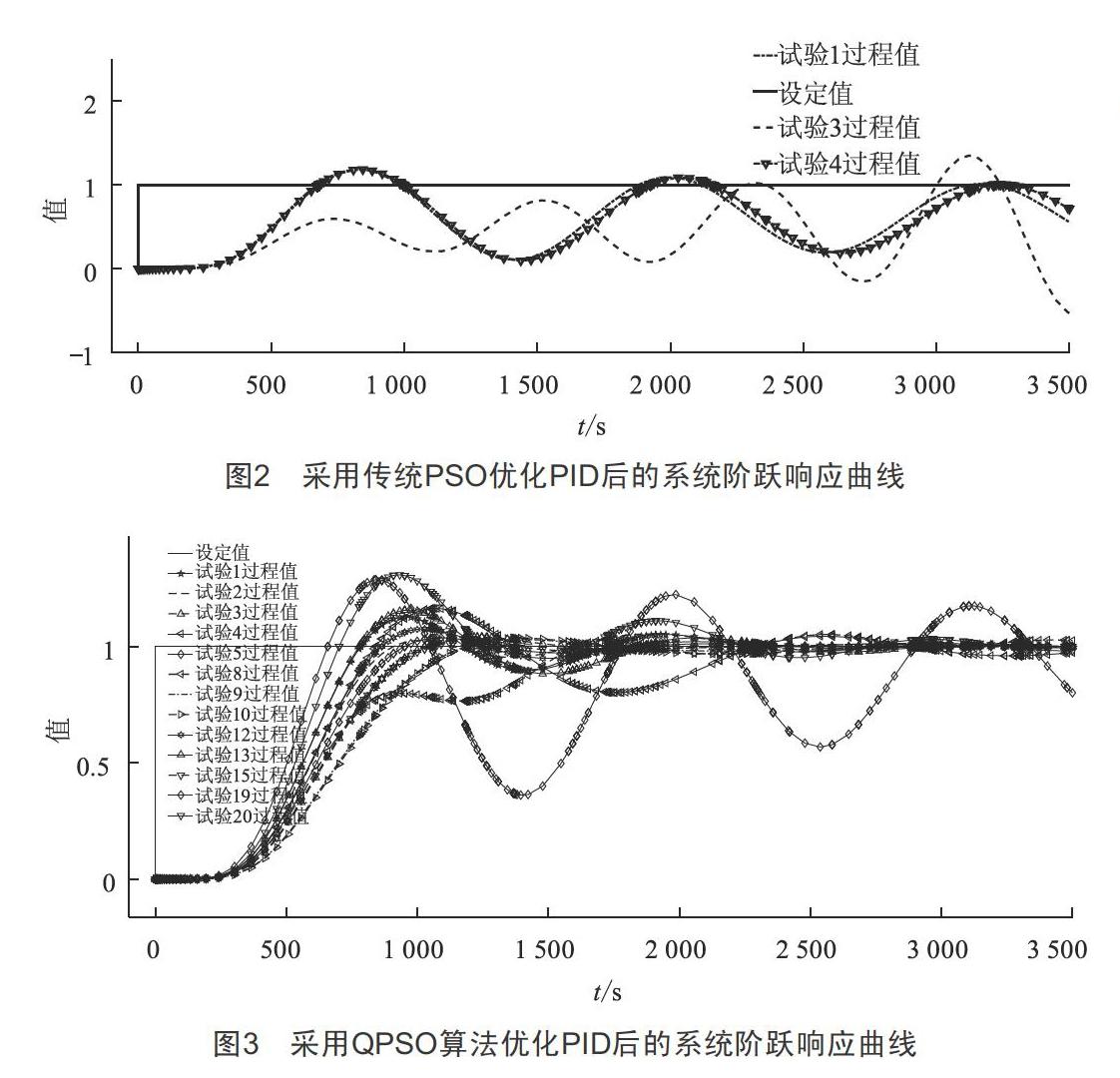
采用傳統PSO算法優化再熱汽溫調節系統PID參數后,對系統進行仿真,結果如圖2所示,可見采用傳統PSO算法對再熱汽溫控制系統PID參數進行優化的效果差,甚至會得到令控制系統發散的PID參數,分析其原因為算法在早期迭代中就陷入了局部極值,無法尋求更優解。
2.4? ? QPSO算法優化再熱汽溫調節系統PID參數
鑒于上述采用傳統PSO算法優化再熱汽溫調節系統PID參數的效果不佳,將優化算法改為QPSO算法,粒子群的種群范圍為[10,500,500],最優的PID參數約為Kp=0.713,Ki=0.001 6,Kd=104,其最優目標值為236 960。20次優化過程得到最優目標值小于2.4×105的次數為8,因此尋找到最優解的概率為40%。用所得的20組PID參數對系統進行仿真,結果如圖3所示,可見采用QPSO算法對再熱汽溫控制系統PID參數進行優化的效果良好,不會尋優到導致系統發散的PID參數,具有不錯的克服算法陷入局部最優解的能力,但通過試驗發現算法收斂速度較慢,普遍需要種群進化150代后才能收斂。
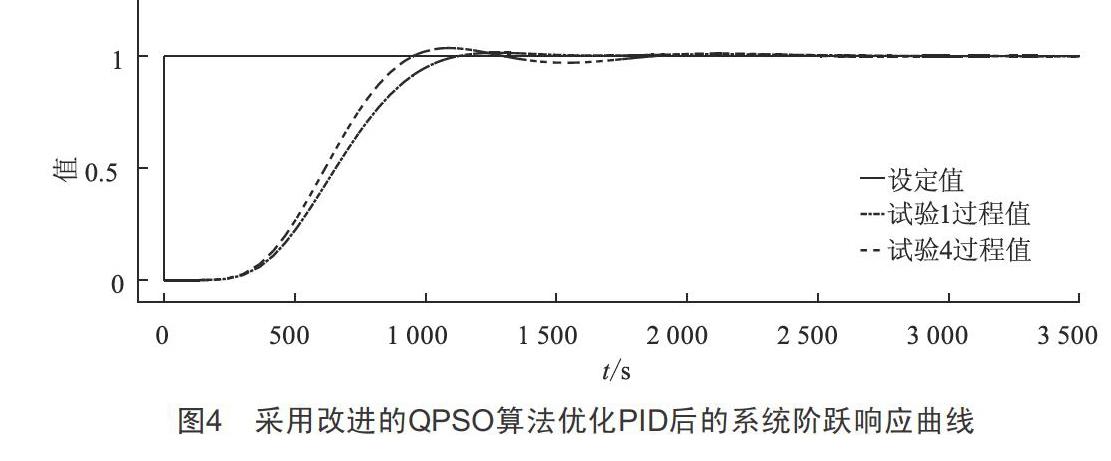
2.5? ? 改進QPSO算法優化再熱汽溫調節系統PID參數
為進一步提升QPSO算法的尋優能力和收斂性能,本文對QPSO算法進行了改進,并采用該改進QPSO算法優化再熱汽溫調節系統PID參數,粒子群的種群范圍為[10,500,500],最優的PID參數約為Kp=0.713,Ki=0.001 6,Kd=104,其最優目標值為236 960。20次優化過程得到最優目標值小于2.4×105的次數為19,因此尋找到最優解的概率為95%。選取19組最優PID參數中的任意一組與剩余一組非最優PID參數,對系統進行仿真,結果如圖4所示,即使試驗1所得PID參數非最優,但其最優目標值為267 415,種群有效地向最優解收斂,因此采用該組PID參數的控制效果良好,可見采用改進QPSO算法對再熱汽溫控制系統PID參數進行優化的效果優異,且算法普遍在種群進化至60代時已經收斂,與QPSO算法相比,增加了種群在算法中期的粒子多樣性,具有更強的克服算法陷入局部最優解的能力和收斂能力,在保證尋優效果的同時,大大縮短了尋優時間。
3 結語
本文通過分析采用傳統粒子群算法和傳統量子粒子群算法進行PID參數尋優過程中的優缺點,提出了一種引入擾動函數的改進QPSO算法,將改進的QPSO算法運用于再熱汽溫調節系統的PID參數優化,對優化后的控制系統進行階躍擾動仿真試驗,并與工程上的臨界比例度法、傳統粒子群算法、傳統量子粒子群算法自整定的仿真結果對比,結果表明:將改進的QPSO算法運用于火電廠再熱汽溫調節系統的PID參數優化,具有更加突出的尋優能力和收斂性,使得系統具有優良的調節質量,既節省了人工整定PID參數的大量精力,又消除了因整定效果不佳而造成的系統振蕩等危險因素。
[參考文獻]
[1] 黃少榮.粒子群優化算法綜述[J].計算機工程與設計,2009,30(8):1977-1980.
[2] 朱蓉,靳雁霞,范衛華.融合優質粒子分布的粒子群優化算法[J].小型微型計算機系統,2015,36(3):576-580.
[3] 許志良,曾徳爐,張運生.一種結合次梯度的粒子群全局優化算法[J].計算機應用研究,2015,32(4):1007-1010.
[4] 印桂生,崔曉暉,董宇欣,等.面向離散優化問題的改進二元粒子群算法[J].哈爾濱工程大學學報,2015,36(2):191-195.
[5] Sun J,Feng B,Xu W B.Particle swarm optimization with particles having quantum-behavior[C]//Proceedings of 2004 Congress on Evolutionary Computation,2004:325-331.
[6] Sun J,Feng B,Xu W B.A global search strategy of quantum-behaved particle swarm optimization[C]//
Proceedings of IEEE conference on Cybernetics and Intelligent Systems,2004:111-116.
[7] 楊紅月,谷俊杰.再熱汽溫控制系統數學模型的建立與實驗分析[J].電力科學與工程,2011,27(6):51-56.
收稿日期:2020-03-03
作者簡介:劉錦廉(1987—),男,福建龍巖人,碩士,工程師,研究方向:智能算法在模型識別及過程控制方面的應用。

