電網阻抗對光伏電站諧波過電壓的影響

趙鵬程

（黃河水電物資有限公司，青海 西寧 810003）

0 引 言

近年來，太陽能發電技術發展迅速，成本下降，全球范圍內大規模的光伏應用使光伏發電成為最具有發展前景的發電技術[1]。光伏發電安全可靠，不需要額外的燃料消耗，無污染，維護簡單，受地域限制較小，可大規模集中發電，也適宜分散發電。光伏發電主要包括分布式光伏發電和太陽能熱電發電，我國主要采用光伏發電[2]直接將光能轉化為電能[3]。

本文基于光伏電站無源網絡模型，分析了逆變器的輸出導納特性，并依據實例從時域、頻域分別分析電網阻抗對光伏電站諧波過電壓的影響。

1 光伏電站無源網絡模型

本文選擇青海烏蘭某光伏電站的拓撲，推導其無源網絡模型。光伏電站采用兩級升壓模式，光伏發電單元經一級升壓變后匯集到10 kV母線開關，10 kV母線接入主變壓器（1#主變容量為31.5 MVA），低壓側升壓至110 kV，并由110 kV線路送至330 kV變110 kV側，接線形式為單母線接線。為了使得到的結果具有通用性，推導過程中，光伏單元數使用參數n描述，集電線路用m描述。光伏電站結構如圖1所示。

依據前文所述進行等效，可得到光伏電站與集電線路等效阻抗圖，其中，集電線路等效阻抗圖如圖2所示。

圖2中，ZN為逆變器及其LCL濾波器等效阻抗；Zt1、Zt2、Zt3分別為雙分裂變壓器的原邊繞組及兩個副邊繞組的等效阻抗；Zdi和Ydi（i=1,2…,n）分別為單條集電線路的第i個發電單元后連接的電纜線路的等效阻抗和導納；ZT和YT分別為光伏電站升壓變壓器的等效阻抗和導納；ZS為該光伏電站并入的大電網的等效阻抗。

諧波傳遞拓撲的節點導納矩陣Y是一個4mn+2階的方陣。

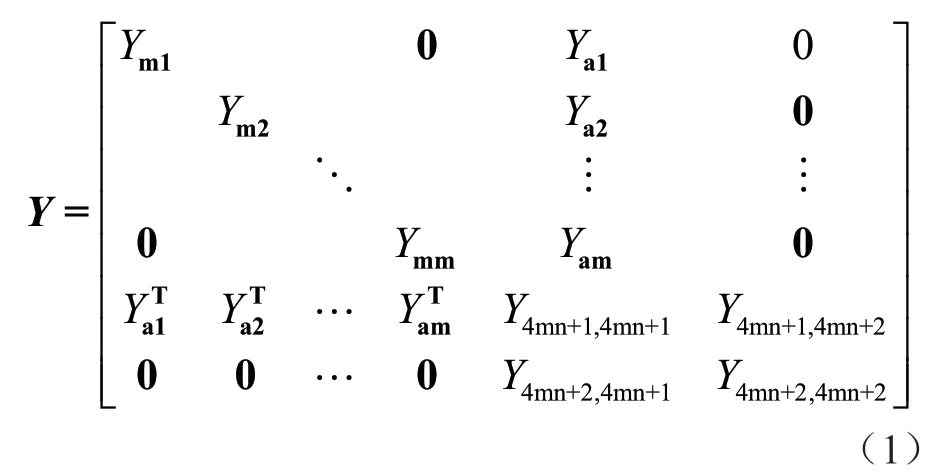
其中：Yai為4n×1階列向量。

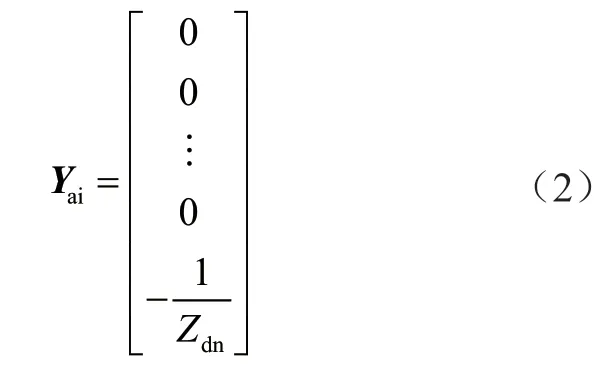
式中：Zdn為每條集電線路的最末端一段電纜。

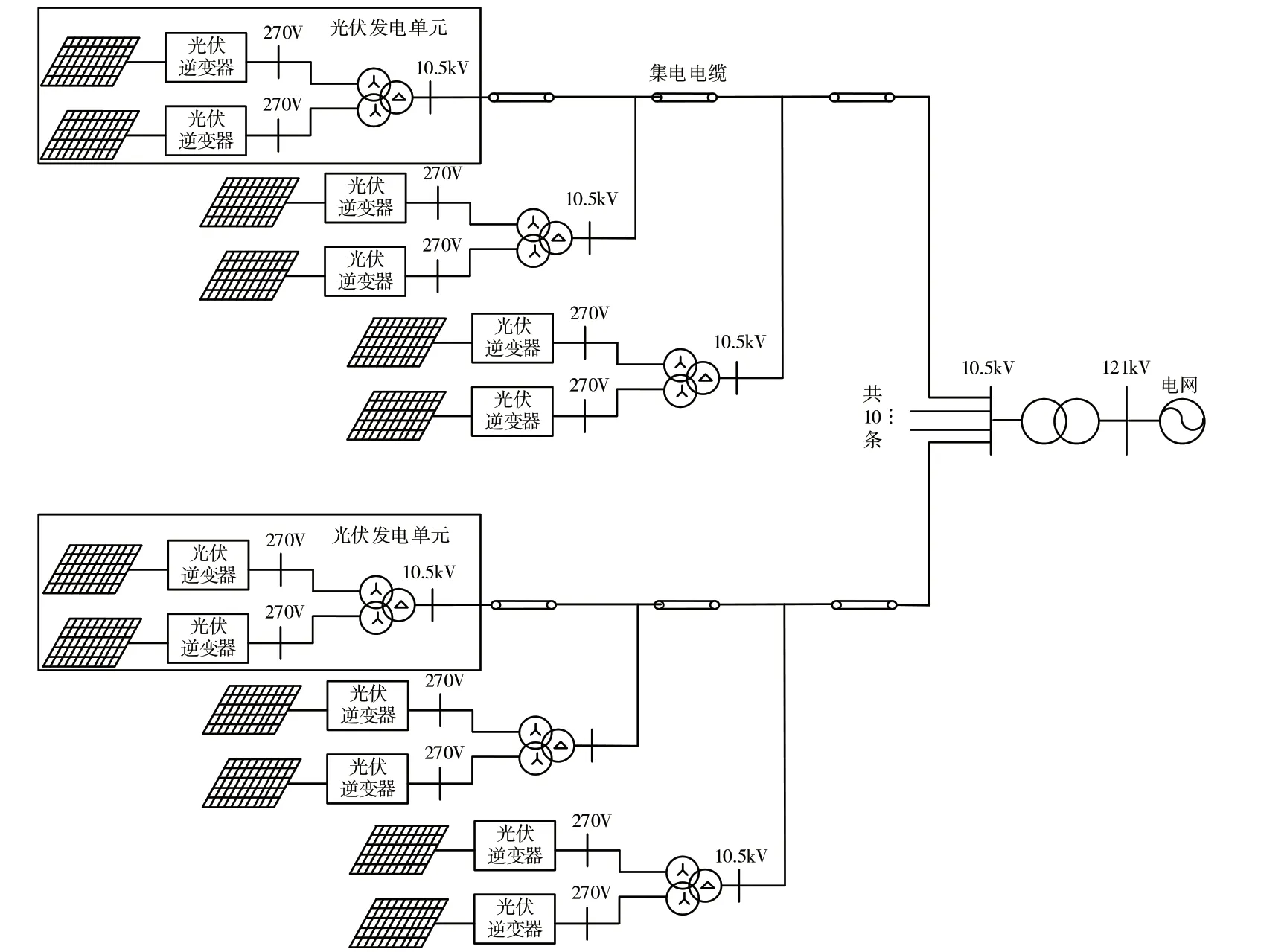
圖1 青海烏蘭某30 MW光伏電站拓撲結構圖

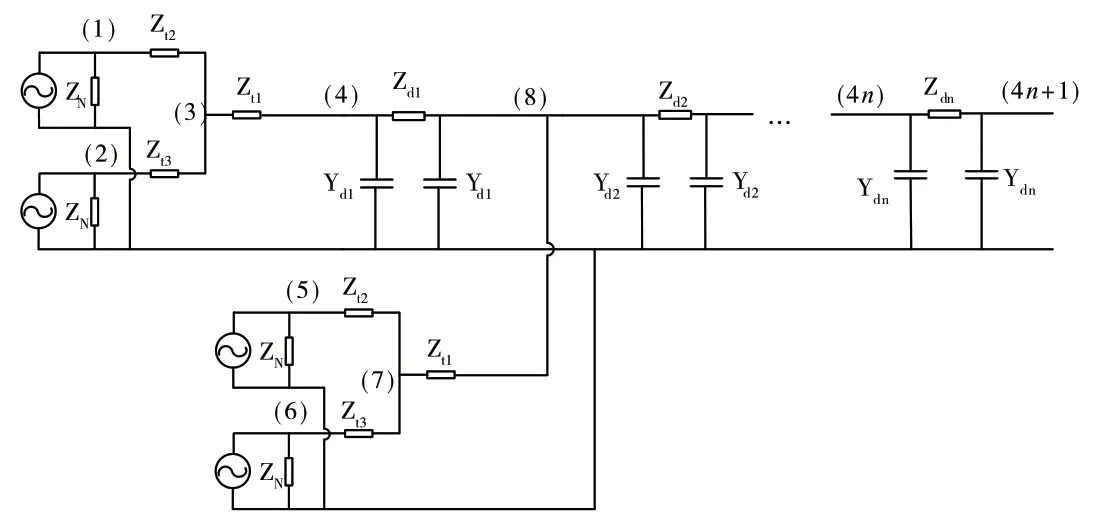
圖2 集電線路等效阻抗圖

Ymi(i=1,2…,m)為第i條集電線路的節點導納矩陣，其為4n階方陣，則：

式中，Y1、Y2為4階方陣，其中，方陣Y1為整個支路中第一發電拓撲節點及與本節點有關電纜的導納矩陣總集，Y2為整個支路除第一發電拓撲節點外的發電節點和跟這些發電拓撲節點相關聯的電纜的導納矩陣總集。為了正確得到舉證Ym，這里將定義Yb的補充矩陣為矩陣Yc。可得：

方陣Yi(i= 2,3…m)除Yi(4,4)的位置的值與方陣Y1一式一樣，集電網絡單支路第i個(i= 2,3…n)發電網絡的節點導納矩陣Yi為：

Yc為4n階對稱方陣，有

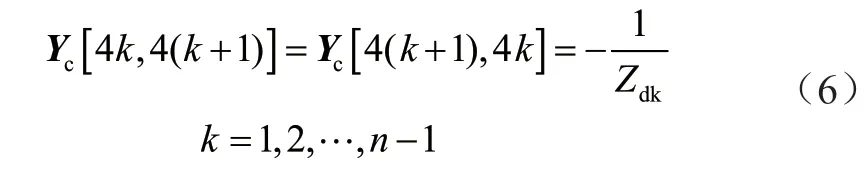
本文諧波潮流的計算方法與基波潮流計算方法如出一轍，通過由諧波傳遞所對應的節點Y導納矩陣和與諧波源的每個節點相對應的諧波電流勾出潮流方程，因此，用所述網絡的方程式來總結每個節點的諧波電壓為：

式（7）中，網絡中各個節點h次諧波電壓列向量為U(h)；各節點h次諧波注入電流列向量為I(h)；Z(h)為h次諧波傳遞網絡的節點阻抗矩陣：

式中，Y(h)為h次諧波傳遞網絡的節點導納矩陣。

2 光伏電站諧波過電壓與電網阻抗之間的關系

2.1 光伏電站諧波含量與電網阻抗的聯系

為了找到光伏電站諧振現象是否與電網阻抗有關，分析諧波網絡傳遞函數帶寬的限制因素中的電網阻抗，對電網阻抗和系統諧波含量之間相互影響關系進行分析，討論系統穩定性是否受電網阻抗的影響以及受何種影響，逐步深入分析光伏電站諧波諧振現象。結合第1部分適用于諧波諧振研究的光伏電站無源網絡模型分析，將上述建模方法用于所有并聯逆變器，可以將光伏電站等效為諾頓模型。運用諾頓定理使分裂變壓器等效電感、光伏逆變器的等效電路進行等效變換。圖3為簡化后進行的光伏電站等效電路。

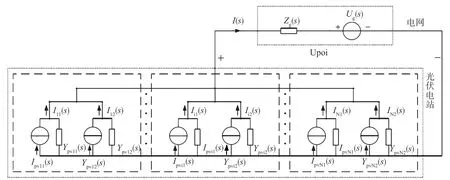
圖3 光伏發電二端口網絡等值簡化結構

圖3中，Ipvi1(s)和Ypvi1(s)為光伏發電站中第i個單元網絡中逆變器的等效參考電流和等效簡化導納，可表示為：

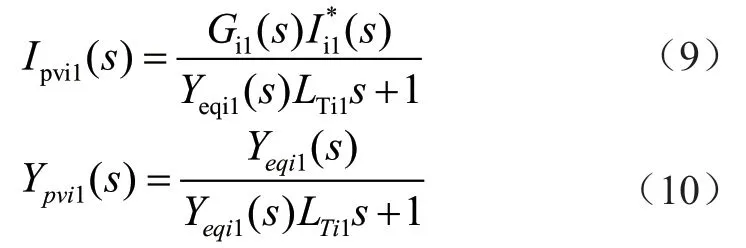
從圖3中可以看出，光伏發電系統利用電網阻抗之間的耦合和分裂變壓器等效電感，使得該系統的所有并聯逆變器之間以及該系統和電網之間存在相互作用。第i個單元模塊中逆變器j的并網電流可通過疊加原理推導出公式（11）：

在此推導公式中，電網的導納可表示為：

本文將采用擾動量為公式（13）：

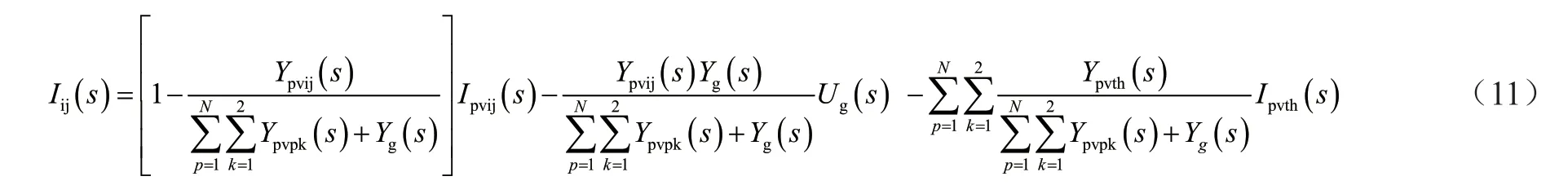
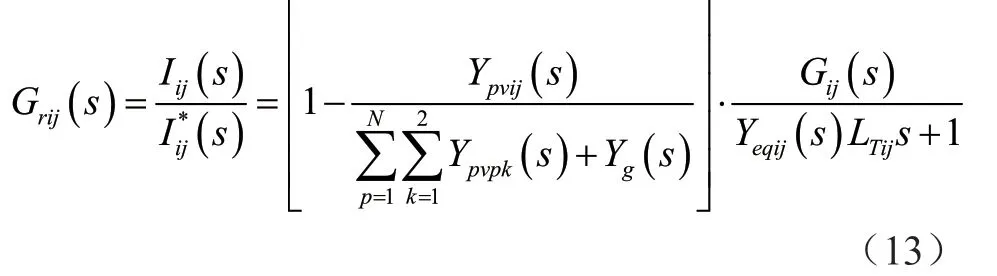
通常在光伏發電系統中采用的逆變器拓撲和逆變器閉環控制方法相同，本文對各個逆變器提出一些假設。假設各項參數和指標以及逆變器的控制策略一毫不差時，式（13）可以簡化為：

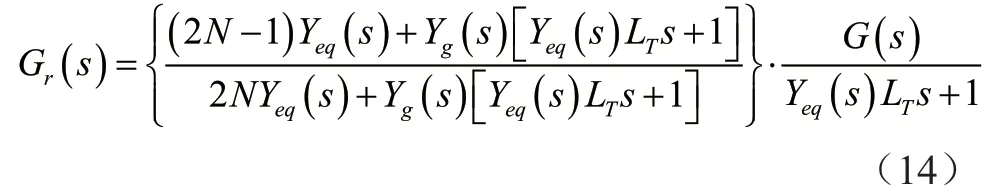
想要使電網阻抗影響網絡的傳遞函數諧振頻率觀察得更加主觀、清晰，在用軟件進行仿真和實際驗證過程中使用了Bode圖來分析，由式（14）得出開環傳遞函數中存在系統傳遞函數特性的影響因素。

將供電系統的阻抗加入光能并網逆變器，發電系統中傳輸電流相對應的函數對數頻特性僅包含諧振峰，該諧振峰是存在于諧振頻率處的。光能發電廠多個逆變器的并聯連接，存在兩個共振峰。從具有定頻率的諧振峰到另一個諧振峰的諧振頻率會根據系統阻抗和光能發電廠的功率的變化而變化。Gr(s)的帶寬和諧振頻率會受到電力網絡阻抗中等效電感L的影響，會隨L的上升而下降。電網增加等效電阻會提高抗諧振性能，并抑制諧振峰值，進而提高整個系統的動態穩定性。電網等效阻抗的其中一影響因素為發電單元的容量V，其大小會隨V的增大而增大。當V增大時，Gr(s)的帶寬和系統的諧振頻率會隨V的增大而減小。與此同時，系統加強了抗共振峰的力度，并且系統的穩定性隨之提高。

為方便對上述結論進行驗證，在青海中廣核烏蘭光伏電站的參數及選型的基礎上，對部分參數進行適當整定，以更好地適應就電網阻抗對光伏電站諧波諧振影響的分析。由于光伏電站采用的逆變器均為同一型號，各發電單元的外特性大致相同，因集電線路長短不同帶來的影響予以忽略，因此可選擇任一逆變器作為研究對象。

當光發電系統中逆變器并網時諧波電流的THD為1.92%時，相對應的電力網絡中阻抗等效電阻RL和等效電感L分別為3.2 mΩ和19.5 μH；當THD變換為1.84%時，相對應的RL和L分別為3.2 mΩ和23.3 μH，此時，對應的光發電并網系統諧振頻率為1 470 Hz和1 550 Hz；當THD變換為2.19%時，相對應的RL和L分別為4.81 mΩ和23.3 μH，此時，對應的光發電并網系統諧振頻率為1 450 Hz和1 550 Hz；當THD由1.92%減小為1.84%時，相對應的L從19.5 μH提升到23.3 μH，此時，諧振頻率由1 470 Hz變換為1 450 Hz。

2.2 并網阻抗對光伏電站穩定運行的影響

光伏電站中，如果電力網絡的阻抗增加，則系統可能會諧振，從而導致整個系統不穩定。因此，必須分析整個系統穩定運行條件下的區域。以兩個級聯子系統的阻抗比是否滿足標準Nyquist穩定性來確定級聯系統的穩定性。采用阻抗穩定性判據非常適合確定級聯系統的穩定性，確定的結果取決于子系統阻抗的實際測量，因此是可靠的、值得信賴的。所以，通過仿真驗證了系統的穩定運行，驗證了分流結果，為抑制光伏電站諧振和所產生的諧波的策略提供了指導和參考。

實際中，為了判定系統的穩定性，可通過測量光能發電系統和兩個級聯子系統阻抗，利用Nyquist判據判斷光伏電站最小環路增益是否包圍(-1,j0)點，從而判定系統穩定性。

3 結 論

本文推導了光伏逆變器的諾頓模型，分析逆變器的輸出導納特性，評估其導納可能的取值范圍，并以青海烏蘭某光伏電站拓撲為例，推導出適用于諧波過電壓分析的無源網絡模型。結合模型明確了電網阻抗對光伏電站諧波過電壓的影響，分別從時域和頻域角度，對其進行研究。