ANSYS在索道線路計算分析中的應用

賀宇龍， 張 爭

(中國恩菲工程技術有限公司， 北京 100038)

0 概況

架空索道具有自然地形適應性強、爬坡能力大、占地面積少、受氣候影響小等特點，近年來在我國景區及滑雪場中已得到廣泛使用。在對索道線路設計時，一般采用傳統的理論計算公式方法設計。當索道鋼絲繩采用兩端錨固時，傳統設計方法往往忽略索道支架位移對鋼絲繩拉力的影響。有限元計算軟件的出現為鋼絲繩及支架的計算提供了新的途徑。本文以某架空索道為例，采用ANSYS有限元軟件對鋼絲繩及支架進行整體建模，計算鋼絲繩在各種受力狀態下的應力和位移分布狀態，并與理論計算結果進行對比分析。

某架空索道是一條救援演習索道，線路水平距離為80.76 m，共設置兩個支架，支架高度分別為9.5 m(1號支架)和17 m(2號支架)。支架之間設有兩根鋼絲繩，采用圓股鋼絲繩，該鋼絲繩繞過支架上的鞍座錨固在支架兩側的錨固基礎上。鋼絲繩彈性模量為1.2×105MPa。在其中一根鋼絲繩的跨中放置1個六人吊廂，距離1號支架40.38 m；在另一根鋼絲繩的跨中放置1個雙人吊椅，距離1號支架40.38 m。六人吊廂側鋼絲繩直徑42 mm，截面面積為728 mm2。雙人吊椅側鋼絲繩直徑36 mm，截面面積為519 mm2。索道支架采用單筒支架，主要由塔身和橫擔等結構通過螺栓或焊接連接而成。支架鋼結構材料采用Q345B，密度7 850 kg/m3，彈性模量為2.06×1011Pa，泊松比為0.3，索道線路配置圖如圖1所示。

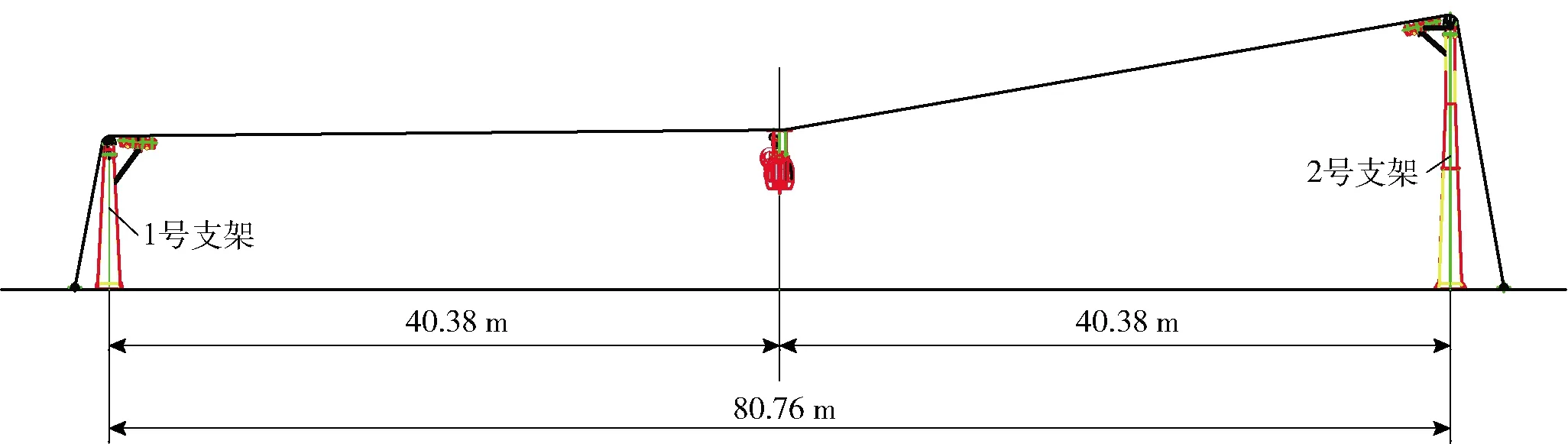
圖1 索道線路配置圖

1 索道線路計算

由于該架空索道下方有建筑物，所以該索道對垂直凈空以及撓度有嚴格的要求。根據《采礦設計手冊(礦山機械卷)》第八章關于兩端錨固的承載索拉力的計算公式(如公式(1)所示)和第六章關于承載索撓度的計算公式(如公式(2)所示)[1]，承載索的拉力和撓度可根據以下公式確定。

圖2 鋼絲繩模型圖

(1)

式中Tjx—載具距跨端x距離處的承載索平均拉力，kN；

Tjm—載具位于跨距中點時承載索最大平均拉力，kN；

E—鋼繩的彈性模數，MPa；

F—鋼繩的金屬斷面積，mm2；

x—載具距跨端的水平距，m；

l—跨距，m；

ε—鋼的線膨脹系數；

G—跨距內的承載索重力，kN；

Qm—和Tjm對應的位于跨距中點的集中荷載，kN；

Qx—距跨端x時的集中荷載，kN；

tmin—環境最低氣溫，℃；

tx—貨車運行當時氣溫，℃；

α—弦傾角，(°)。

(2)

式中fx—考察點的撓度，m；

Tj—兩支架上承載索最小拉力的平均值，N；

q0—承載索每米重力，N/m；

Qz—重車側集中載荷，N；

K—撓度系數，這里取為1。

通過公式(1)、(2)可以計算出空載工況和滿載工況下的鋼絲繩拉力和跨中最大撓度。為了驗證計算結果的準確性，下面采用有限元軟件對該結構進行計算對比。將六人吊廂和雙人吊椅的吊點作為鋼絲繩的位移控制點來進行對比分析，控制點的位置數據如表1所示。

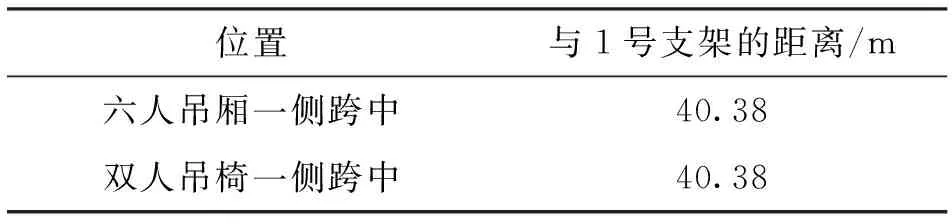
表1 位移控制點

2 有限元模型建立

本文采用通用有限元軟件ANSYS對該結構進行建模計算[2]，主要建立只考慮鋼絲繩的鋼絲繩模型和考慮鋼絲繩及支架的整體模型兩種計算模型。采用BEAM188單元模擬塔身和橫擔，LINK10單元模擬鋼絲繩結構，LINK10單元獨一無二的雙線性剛度矩陣特性使其成為一個軸向僅受拉或僅受壓桿單元。當使用只受拉選項時，如果單元受壓，剛度就消失，以此來模擬鋼絲繩的松弛，可以很好模擬鋼絲繩的特性，材料按彈性狀態進行計算。對于整體模型來說，可以認為鋼絲繩與鞍座無相對位移，鋼絲繩的水平力主要由支架承擔，整體模型可簡化為鋼絲繩固定在支架橫擔兩端，有限元計算模型如圖3、圖4所示。

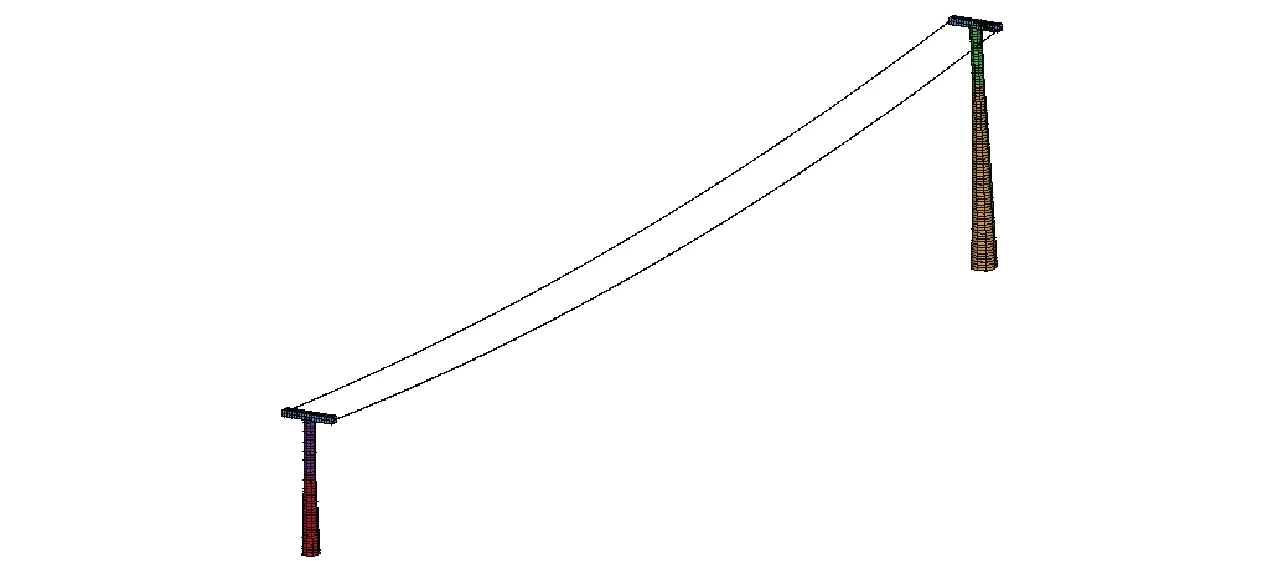
圖3 整體模型圖

圖4 鋼絲繩模型位移云圖

3 鋼絲繩結構找形

鋼絲繩結構找形指確定鋼絲繩結構在承受荷載作用之后的形狀，由于鋼絲繩結構其自身剛度很小，承受荷載之后會發生很大的變形，平衡方程也需要在變形后的位置上建立，所以應對鋼絲繩的初始狀態進行找形。上文中理論計算得出了鋼絲繩在僅承受自重和鋼絲繩拉力條件下的最終形態，以此種狀態下的鋼絲繩結構線形為目標值，經過反復迭代計算，使結構在僅受自重和鋼絲繩拉力的狀態下，給定初始鋼絲繩拉力使得結構幾乎不發生位移變化，即完成了找形，整體模型找形結果如圖5、圖6所示。

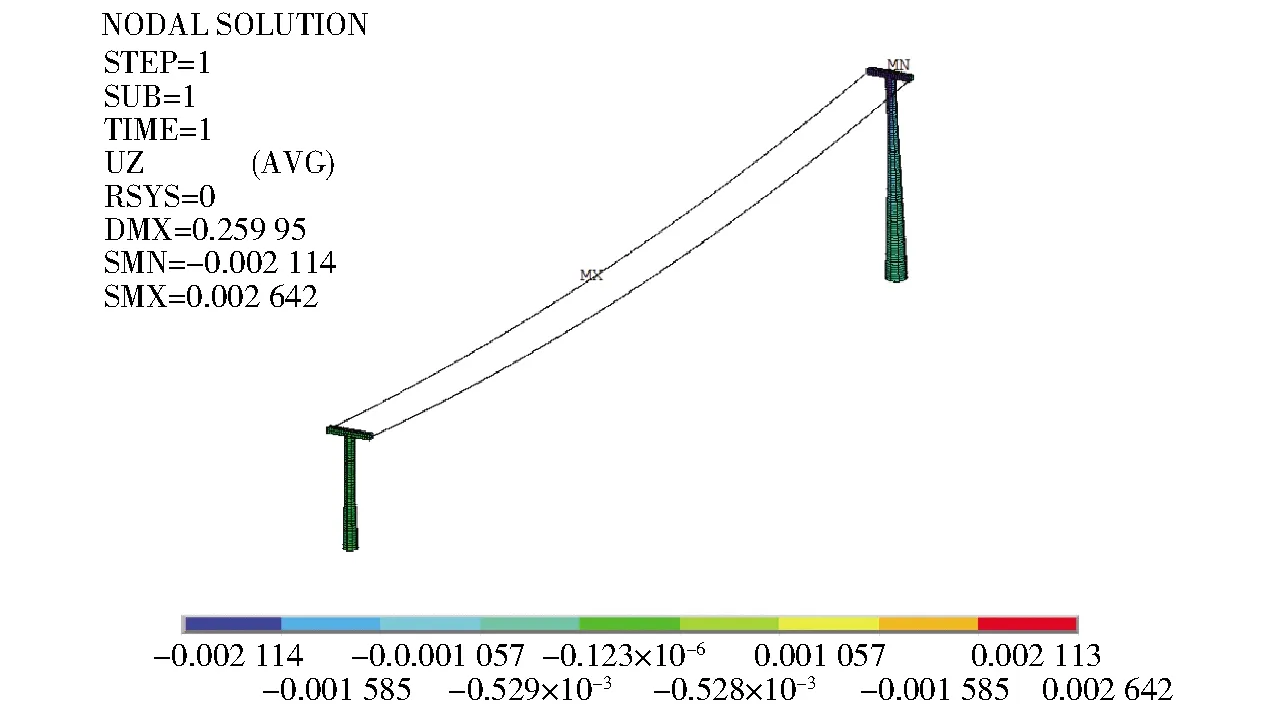
圖5 整體模型位移云圖

圖6 空載工況鋼絲繩模型拉力云圖

為了驗證模型的計算結果，將找形后的鋼絲繩拉力和撓度與理論計算的結果進行對比，如表2、表3所示，通過對比可以發現有限元軟件計算的鋼絲繩拉力和撓度與理論計算的結果基本保持一致，也說明了找形結果是穩定可靠的。

表2 鋼絲繩拉力計算比較

表3 初始態各位移控制點撓度值計算比較

4 荷載與工況

本工程主要考慮索道空載和滿載兩種荷載工況，空載工況是鋼絲繩僅承受載具的重量，滿載工況為鋼絲繩承受載具和乘客的重量。計算時考慮了降溫30 ℃的溫度荷載作用。由于本工程為救援演習索道，載具均固定在鋼絲繩上，相對位置固定，暫不考慮風荷載的作用。載具的荷載通過節點荷載進行施加，溫度荷載通過體荷載進行施加。以找形之后的計算模型為基礎，將荷載施加在模型中，即可計算出各工況下的鋼絲繩拉力和位移結果。

5 鋼絲繩計算結果分析

通過ANSYS軟件分別對鋼絲繩模型和整體模型進行有限元計算[3]，得到該結構在空載和滿載兩種工況下的計算結果，如圖7～圖10所示，由于計算結果較多，這里僅列出了空載工況下的結果。通過對計算結果進行總結歸納，得到兩種模型的有限元和理論計算結果的比較，鋼絲繩拉力計算結果比較如表4所示，跨中撓度計算結果比較如表5所示。

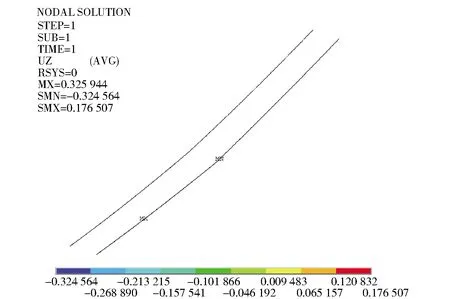
圖7 空載工況鋼絲繩模型拉力云圖

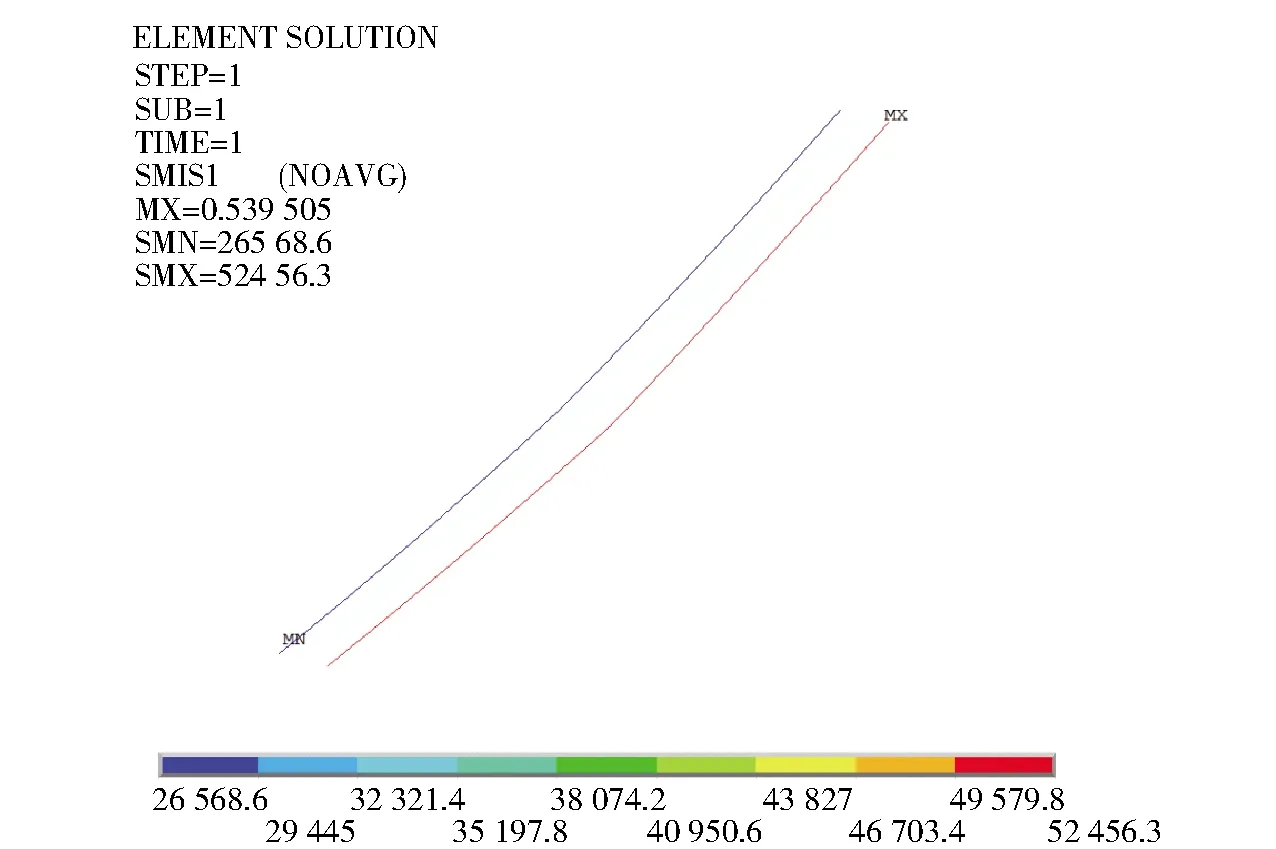
圖8 空載工況整體模型鋼絲繩拉力云圖

圖9 空載工況整體模型鋼絲繩拉力云圖

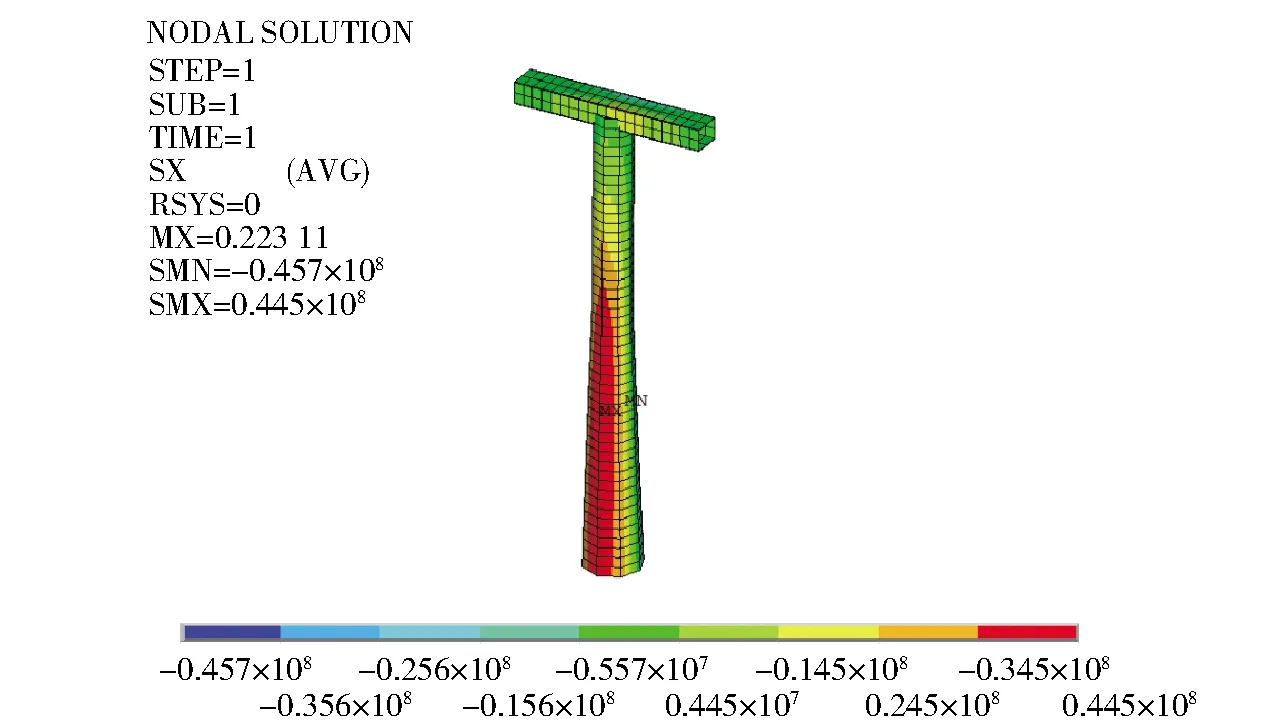
圖10 1號支架應力云圖

通過對表4、表5的分析，從總體上可以看出，理論計算和有限元計算的結果較為接近。其中計算鋼絲繩拉力時，理論值與鋼絲繩模型計算值的誤差在1.0%～3.3%之間，理論值與整體模型計算值的誤差在9.1%～15.3%之間；計算撓度時，理論值與鋼絲繩模型計算值的誤差在0.1%～1.2%之間，理論值與整體模型計算值的誤差在8.4%～16.1%之間；由此可見，理論計算結果與鋼絲繩模型的計算結果更為接近，這是由于在進行理論計算時，兩端錨固承載索拉力計算公式的邊界條件假定為兩端固定的，鋼絲繩受力時固定端不會發生相對位移，這與鋼絲繩模型的計算邊界條件是較為相似的，計算結果也比較吻合。這也說明了采用相同的邊界條件和計算假定下，有限元軟件可以比較精確的模擬鋼絲繩結構的拉力和撓度分布狀態。

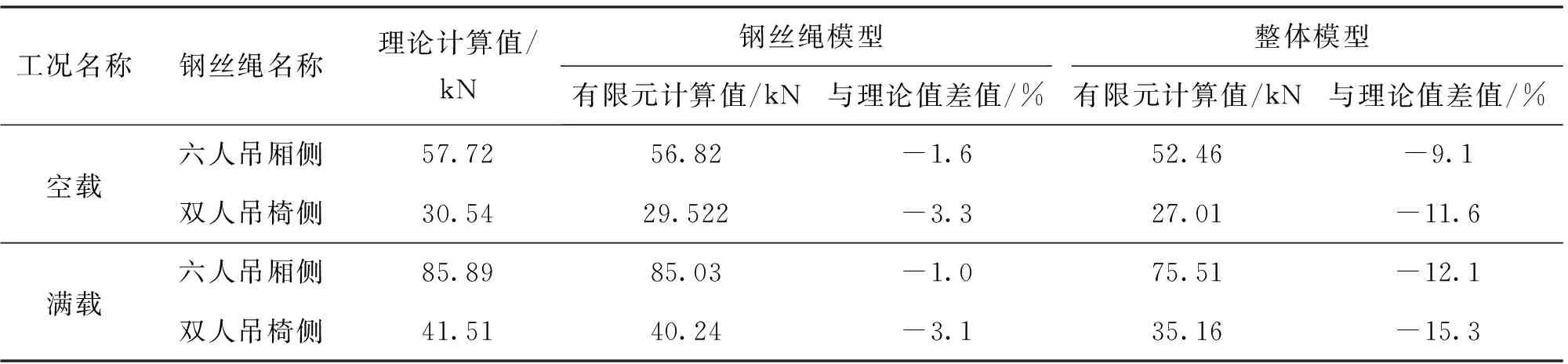
表4 各工況下鋼絲繩拉力結果比較

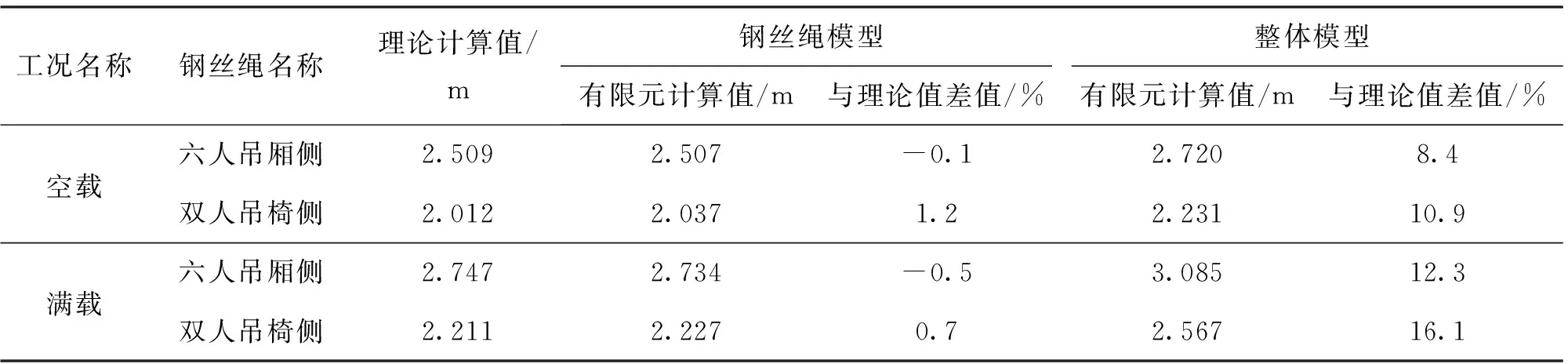
表5 各工況下跨中撓度結果比較

通過理論值與整體模型計算值對比可以發現，整體模型計算結果鋼絲繩拉力值較小，撓度值較大，因為整體模型計算時考慮了支架之間的相對位移以及結構整體的變形協調作用，這樣計算結果與實際情況更為接近。所以在實際設計中，對于此種情況造成的撓度增加應予以考慮。

6 支架計算結果分析

通過對整體模型的計算分析，可以看出索道支架在鋼絲繩拉力的作用下會產生較大的位移，為了驗證支架結構的安全，對1號支架和2號支架也進行了分析。

通過圖11～圖14可以看出1號支架最大應力為44 MPa，最大位移為22 mm；2號支架的最大應力為45 MPa，最大位移為49 mm。根據《GB 12352—2018客運架空索道安全規范》[4]對于索道支架進行驗算，1號、2號支架的最大應力小于其許用應力[5]，支架允許變形沿索道中心線方向小于H/300，滿足鋼結構支架的應力和變形限值要求，結構安全可靠。

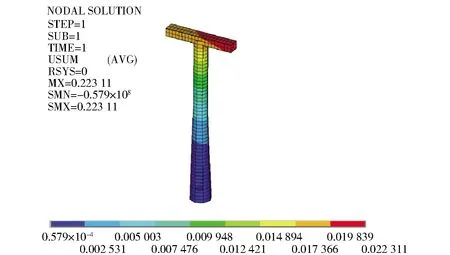
圖11 1號支架位移云圖

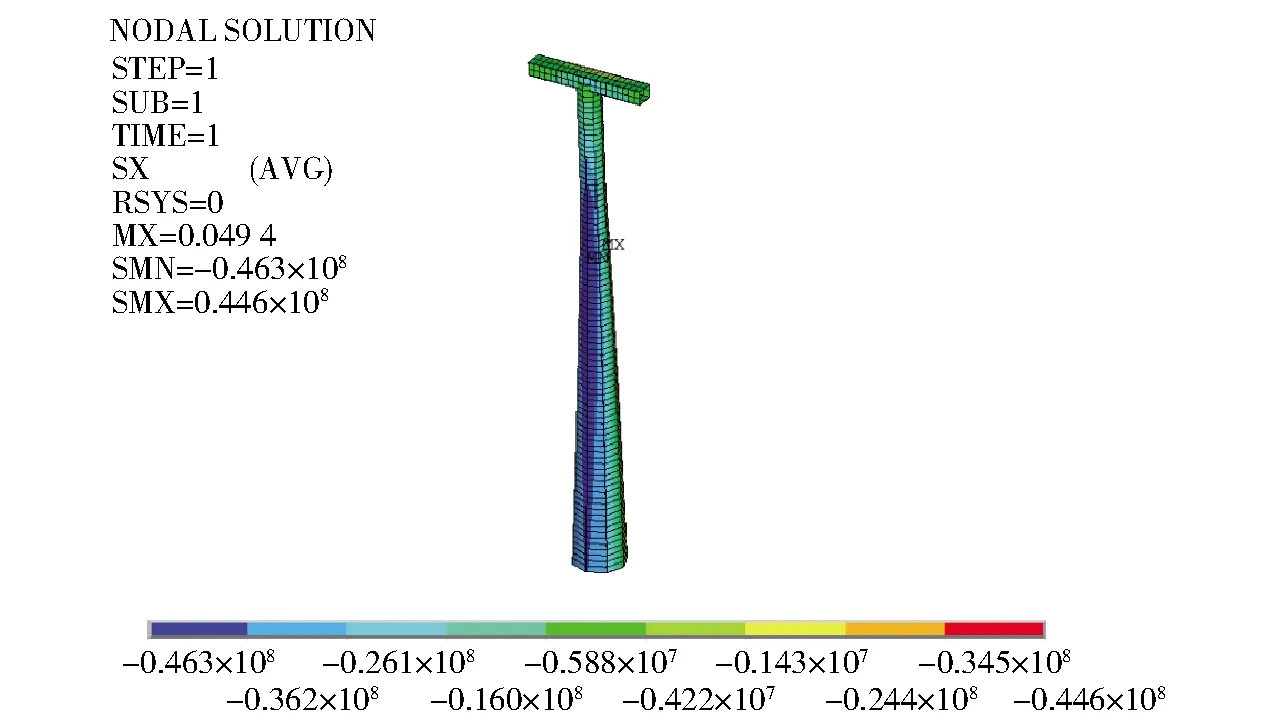
圖12 2號支架應力云圖

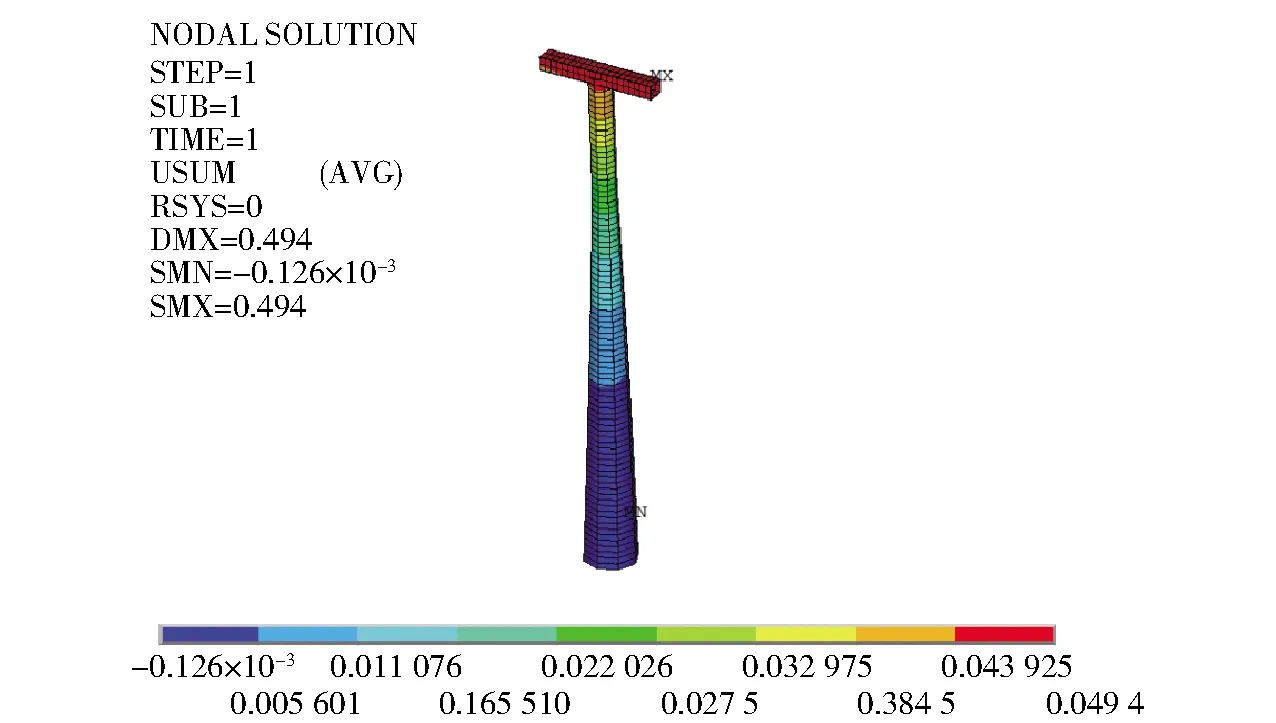
圖13 2號支架位移云圖

7 結論

本文對某架空索道分別進行了理論計算和有限元計算，可以得到以下結論。

(1)本文根據兩端錨固的索道承載索理論計算公式，得出了鋼絲繩拉力和撓度的理論計算值，并且通過ANSYS有限元計算軟件，分別建立了只考慮鋼絲繩的模型和考慮鋼絲繩、支架的整體模型兩種計算模型，通過理論值與有限元計算值的對比，得到鋼絲繩模型的計算結果與理論值較為接近，可見在邊界條件相同的條件下，有限元軟件可以較好地模擬索道的線路計算。通過有限元計算分析，可以得到索道線路任意點的撓度和拉力值，計算結果更加全面、清晰。

(2)兩端錨固承載索拉力的理論計算公式忽略了鋼絲繩固定端的相對位移對鋼絲繩拉力和撓度的影響。采用有限元軟件可以建立支架和鋼絲繩的整體模型，可以計算出支架變形對鋼絲繩拉力和撓度的影響，所以計算結果與實際較為接近。

(3)通過建立鋼絲繩和支架的整體模型，能比較準確計算出支架的應力和位移的分布狀態，經驗算支架應力和變形均滿足相關規范要求。

(4)文中所述的設計方法能夠全面準確分析支架在各工況的受力狀態，其結構也為以后類似工程提供了參考。