不同gkv下耦合Chay神經元模型放電節律及其分岔分析

楊永霞 李玉葉

摘 要：本文用數值仿真方法得到鉀電導系數gkv取不同值時，興奮性化學突觸誘導的耦合Chay神經元模型的放電節律有DB簇放電和周期簇放電。并利用快慢變量分離機制和分岔分析方法揭示放電簇的類型主要有“fold/fold cycle”滯后環的“Hopf/fold cycle”型簇和“fold/fold cycle”型簇。

關鍵詞：電導系數;Chay神經元模型;快慢變量分離;分岔分析

中圖分類號：O193? 文獻標識碼：A? 文章編號：1673-260X（2020）09-0010-03

1 引言

神經系統是由數以億計的神經元組成的復雜信息網絡，直接或間接參與調節和控制人體內器官、系統功能和生理過程的進行，使人體適應內外環境的變化。神經元的放電活動和信息編碼在神經系統活動中起著重要作用，神經元的數學模型可以模擬仿真神經元的放電活動。Chay神經元模型是神經系統中基于與Ca2+有關的K+離子通道而建立的理論模型，可以很好地仿真可興奮性細胞如心肌細胞、感覺末梢細胞、神經起搏點細胞等的放電節律。耦合Chay神經元網絡產生的主要節律性活動是簇放電，不同模式的簇放電取決于不同濃度的離子電流及不同離子通道的電導系數。電導系數為電導的上限，它與細胞內離子電流的值成正比關系，對神經元膜電位的產生和轉變有重要的作用。

近期，不同離子電流及電導系數對Chay神經元放電節律影響的研究已經取得一定成果。如2015年，李莉等以EC作為分岔參數，以代表鉀離子門控通道時間常數的相關參數？姿n作為條件參數進行仿真，在Chay神經元單模型中模擬到了各種周期放電和混沌放電節律，倍周期分岔到混沌和加周期分岔等，并區分了簇放電和峰放電[1]。王聰迪通過數值仿真與理論論證的方法研究了Chay神經元模型和耦合Chay神經元系統的放電模式以及同步節律[2]。張素麗選取EK和g1作為分岔參數，利用非線性動力學基本理論對Chay模型進行了分岔分析，研究了參數連續變化時模型的動態特性[3]。

對Chay神經元單模型和耦合模型的放電節律的研究較多[4-6]，但對化學突觸誘導的耦合雙神經元網絡放電節律的仿真還很少。本文選取鉀電導系數gkv作為分岔參數，研究耦合雙神經元網絡的放電節律，并利用快慢變量分離和分岔分析揭示不同簇的動力學機制。

2 興奮性化學突觸誘導耦合

Chay神經元模型及快慢變量分離介紹。

2.1 耦合神經元模型

（4）式是化學突觸表達式，其中si與Vj有關，實現了神經元間的耦合。式中s∞（Vj）=■。模型中的部分參數設置為：EC=250.0mV，gs=10.0mS，Esyn-e=-15mV，該突觸是興奮性突觸。？姿n=225.8，？茲s=-35，？滓s=-2。時間單位是ms，電壓單位是mV。

2.2 耦合神經元模型的快慢變量分離

對于上述描述的耦合神經元模型，公式（3）描述的變量Ci（i=1，2）為慢子系統。研究神經元i的簇放電的快慢變量分離，選C=C1=C2為慢變量，其余6維方程為快子系統。首先研究快子系統平衡點和極限環的分岔，后將神經元i的簇放電軌跡的相圖疊加到快子系統的分岔圖上，通過軌線和分岔的位置識別不同模式的簇。

3 主要仿真結果

3.1 不同gkv下耦合Chay神經元模型的放電節律

gkv是依賴電位的K+離子通道中的最大電導。分別取gkv=1100mS、1200mS、1900mS和2200mS，得到耦合Chay神經元模型放電節律分別為DB簇放電、周期83簇放電、周期4簇放電和周期1簇放電，分別如圖1（a）、1（b）、1（c）和1（d）所示。

從圖1可以看出，當gkv=1100mS時，耦合神經元的放電節律為DB簇（圖1（a）），隨著gkv增大，耦合神經元表現為高周期簇放電（圖1（b）），隨著gkv繼續增大，簇內峰的個數減少（圖1（c）），直到gkv=2200mS，耦合神經元為周期1簇放電（圖1（d））。

3.2 不同gkv下耦合Chay神經元模型放電節律的分岔分析

分別對gkv=1100mS、1200mS、1900mS和2200 mS時耦合Chay神經元1的DB簇放電、周期83簇放電、周期4簇放電和周期1簇放電進行快慢變量分離和分岔分析。

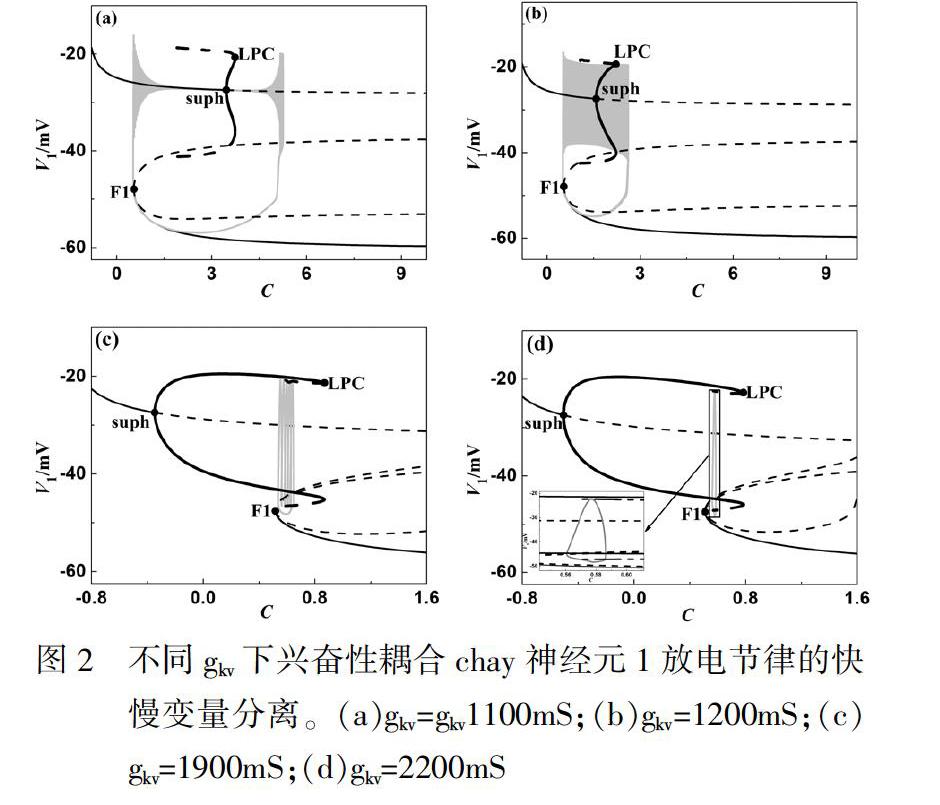
當gkv=1100mS時，快子系統的平衡點和全系統簇放電（如圖1（a）所示）軌線（灰色實線）在（C，V1）平面上的疊加如圖2（a）所示。由圖2（a）可知，在平衡點組成的“Z”型曲線上支，隨著慢變量C增加，不穩定焦點（細虛線）變為穩定焦點（細實線），發生了超臨界Hopf分岔即suph點（C≈3.463），出現了穩定極限環（粗實線）。在“Z”型曲線下支，全系統軌線從靜息態經鞍結分岔F1（C≈0.541）轉遷到上支進入放電。但此時放電簇沒有圍繞穩定極限環發生振蕩，而是圍繞穩定焦點作衰減振蕩，振幅迅速減小到零，當經過超臨界Hopf分岔點suph時，放電簇在不穩定焦點的作用下振幅逐漸增大，當C≈3.740時，穩定極限環與不穩定極限環（粗虛線）相碰，發生了極限環的鞍結分岔（即LPC），上支的放電態轉變為下支的靜息態，放電超出了快子系統的放電區域，根據Izhikevich[7]對放電簇的命名，稱此放電簇為由“fold/fold cycle”滯后環的“Hopf/fold cycle”型簇放電。

當gkv=1200mS時，快子系統的平衡點和全系統簇放電（如圖1（b）所示）的軌線（灰色實線）在（C，V1）平面上的疊加如圖2（b）所示。由圖2（b）可知，在“Z”型曲線上支，隨著慢變量C減小，不穩定焦點（細虛線）變為穩定焦點（細實線），發生了超臨界Hopf分岔即suph點（C≈1.583），出現了穩定極限環（紅色實線）。在“Z”型曲線下支，隨著慢變量C減小，穩定結點（細實線）和鞍點（細虛線）在C≈ 0.538相碰，發生鞍結分岔（即F1），此時全系統軌線從下支的靜息態經鞍結分岔F1轉遷到上支進入放電，放電圍繞穩定極限環（粗實線）振蕩。隨著慢變量C增大，在C≈2.218處，穩定極限環與不穩定極限環（粗虛線）相碰，發生了極限環的鞍結分岔（LPC），上支的放電轉入下支進入靜息，稱此放電簇為“fold/fold cycle”型簇放電，如圖2（b）所示。

當gkv=1900mS及gkv=2200mS時，與gkv=1200 mS時耦合系統的分岔（如圖2（b））類似，形成 “fold/fold cycle”型簇放電，分別如圖2（c）和2（d）所示。

以上分析可以看出，當gkv較小（1100mS）時，耦合Chay神經元1的放電簇為由“fold/fold cycle”滯后環的“Hopf/fold cycle”型放電簇，當gkv較大（1200mS-2200mS）時，耦合Chay神經元1的放電簇均為“fold/fold cycle”型簇放電。

4 討論

耦合Chay神經元模型中的可變參數較多，包括電導系數gI、g1、gkC及反轉電位EI、E1、Ek，當其值不同時，耦合神經元的放電節律也不盡相同。關于各可變參數對耦合神經元放電節律影響的認識有待進一步研究。

——————————

參考文獻：

〔1〕李莉，等.神經起步點自發電節律及節律轉化的分岔規律[J].生物物理學報，2003，19（04）：388- 349.

〔2〕王聰迪.耦合Chay神經元系統的同步研究與應用[D].蘭州交通大學，2019.

〔3〕張素麗.神經元Chay模型的動力學分析[D].太原理工大學，2013.

〔4〕裴利軍，王永剛，范燁.神經元Chay模型的動力學分析[J].鄭州大學學報（理學版），2009，30（02）：7-12.

〔5〕楊卓琴，陸啟韶.神經元Chay模型中不同類型的簇放電模式[J].中國科學（G輯：物理學 力學 天文學），2007，58（04）：440-450.

〔6〕周毅.神經元Chay模型簇放電活動的分岔研究[J].赤峰學院學報（自然科學版）.2012，23（06）：23-25.

〔7〕Izhikevich E. M. Neural excitability， spiking and bursting [J]. Int. J. Bifurcat. Chaos， 2000， 10： 1171- 1266.