空間相似性和旋轉不變性的空間場景匹配研究

房家偉 凌云

摘 要：空間場景與人類生活密切聯(lián)系，無處不在，是人們生活發(fā)生的真實空間。本文針對矢量空間場景匹配過程中的旋轉問題，引入位置圖的概念，分析待匹配場景的內部結構之間的關系，如圖元間的最近點、最遠點、質心點，而這種關系不隨場景的旋轉而變化。突破以往從圖元個體角度描述草圖特征的方法，轉換思路為將空間場景作為群組對象，從整體上刻畫草圖特征。本文以鄭州市局部區(qū)域為實驗數(shù)據(jù)，利用該區(qū)的矢量化數(shù)據(jù)進行驗證，并分析評價匹配結果。實驗結果表明基于位置圖和空間相似性的方法能很好地實現(xiàn)空間場景匹配，并能解決場景旋轉等問題。

關鍵詞：空間相似性;旋轉不變性;位置圖;波形圖;空間場景匹配

中圖分類號：TP391? 文獻標識碼：A? 文章編號：1673-260X（2020）09-0040-05

1 引言

在GIS研究方面，針對空間相似性很多學者一般都用空間幾何關系中的圖元形狀特征、圖元的相對大小特征、兩圖元的相對方向特征、空間關系中的圖元間的拓撲關聯(lián)、圖元間的距離遠近、圖元間的相對方向等來表現(xiàn)[1]。空間相似性關系計算性不高，且空間關系相對復雜，因此在計算空間圖元相似性時要同時考慮空間幾何關系中的形狀特性、大小特性、方向特性;空間關系中的拓撲關系、距離關系、方向關系等多個因子[2]。通過對空間相似性的度量，可以用來揭示空間場景匹配，也對世界的認知提供更多的理論價值和應用價值，因此受到國內外很多學者的研究和關注[1～4]。

探究空間場景匹配問題其實就是計算空間圖元目標實體的相像程度[5]。通常空間場景相似性是將單個圖元的相似關系，以及每個圖元之間的空間關聯(lián)相似性用來建立關聯(lián)圖，計算出相似性[6]。但是此類方法難以解決場景的旋轉問題，從而導致漏查，錯查等結果[7]。因此提出位置圖的計算方法，把輸入數(shù)據(jù)（草圖）看成一個整體，分析其整體關系，包括各圖元間的類空間關系。從而解決匹配過程中輸入數(shù)據(jù)與參考數(shù)據(jù)的旋轉問題。結合草圖數(shù)據(jù)融合的優(yōu)勢，探索面向地理場景的匹配方法，將會進一步提高空間匹配的可用性;進一步揭示地理場景的認知、描述和應用機理;促進地理信息科學和技術的智能化、大眾化、社會化發(fā)展。

2 解決方案

為了提高場景相似性檢索的精度，使用草圖整體特征相似性度量方法，本文首先通過草圖的重心點、最近點、最遠點繪制出幾何位置圖。然后，利用折線相似性計算算法計算出相似性，從而完成粗匹配。最后，結合空間場景的集合相似性和空間關系相似性完成精匹配。

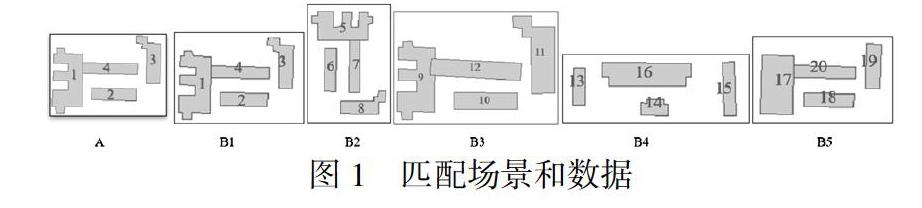
本文選取鄭州市部分地區(qū)的矢量數(shù)據(jù)作為匹配場景進行實驗。圖1中A為匹配場景，圖B1，B2，B3，B4，B5中為數(shù)據(jù)庫。

3 基于位置圖的草圖場景粗匹配

3.1 空間幾何坐標的獲取

每個面狀圖元都可以用一個形狀中心點來表示。通過該點可以從整體的角度來研究旋轉不變性、平移不變性等特征[7]。對于矢量數(shù)據(jù)，大多數(shù)都是用幾何坐標中心點，但是基于本文場景匹配的條件下，需要考慮可能兩個相似度較高的形狀可能幾何坐標點不一致[8]。考慮到幾何目標的面積特征，本文采用重心作為目標的形狀中心點。

但是針對多圖元群組來說，很多學者采用最小外包矩形（MBR）和最小面積外接矩形來描述群組目標。因為相比較于MBR來說，最小面積外接矩形更接近原目標的形狀[6，7]。故本文采用最小面積外接矩形來描述群組。根據(jù)公式（1）求得群組的最小面積外包矩形的質心。

上式中的n為圖元的每條邊與原點組成三角形的面積，Xi，Yi分別表示第i個點在X和Y軸的坐標。基于上述方法得到了空間幾何坐標以及群組目標的最小面積外接矩形質心：

3.2 幾何與力的位置圖繪制與計算

通過群組目標的最小面積外接矩形質心與各圖元間的重心點、最近點、最遠點的關系特征，且這種關系特征特別的靈活，在群組整體發(fā)生旋轉，偏移的時候，能夠很好地度量群組的相似性[9，11]。本文采用位置圖來反映這種圖元間的關系。

由力的位置圖分析可得投影比為一個常量[1]，但是由于用戶輸入等問題，匹配圖形可能會存在旋轉問題，需要再對每個群組做旋轉分析。本文以群組最小MBR的質心為旋轉中心，為？琢°為旋轉角度（0°<？琢<360°）進行旋轉。用相同算法求出投影比。為了直觀方便的反映圖元間的投影比關系，采用波形圖的形式進行展示。

3.3 波形圖相似性的計算

波形圖的X軸坐標的跨度比較大，為0-360;而Y軸的坐標卻是0-20之間[12，13]。針對這個問題，提出了對波形圖進行歸一化得做法：

（1）遍歷所有數(shù)據(jù)，找出X，Y的最大值和最小值;

（2）X，Y的所有值分別減去最小值，然后除以最大值和最小值的差。

根據(jù)上述算法[12-17]，得到波形圖的相似度如下，進行相似程度排序如表2：

通過繪制波形圖可以看出B1和B2、B3具有較高的相似性。但是并不能確定它們就是用戶所要匹配的場景，還可能存在如下可能，因此要做精匹配。

情況一：MBR相同，重心相同，但是圖元不同。見圖2（a）：群組MBR和重心相同。

情況二：群組相同（包括各圖元相同），但是群組整體變大。見圖2（b）：群組等比放大。

情況三：部分圖元確定，部分只是位置稍微偏離。見圖2（c）：部分圖元偏離。

4 基于空間相似性的精匹配

針對粗匹配中出現(xiàn)的問題，本章通過精匹配從粗匹配結果排序中篩選出最可能的空間場景。首先，群組的幾何相似性通過圖元的形狀，大小，方向等幾何特征來描述[18，19];然后，空間場景的空間關系相似度用圖元間的拓撲關系、距離關系、方向關系的相似度來度量[20-25];最后本文用層次分析法，分別對空間場景的幾何相似度及空間關系相似度附以不同的權重，來表示空間場景的總相似性。而相似性是定量衡量空間場景的接近程度，因此可以完成空間場景的匹配[18，19，24]。

4.1 空間場景幾何相似性的計算

空間場景幾何相似性的計算包含了形狀相似性[25]、大小相似度[21]和方向相似度[15]，計算方法見參考文獻，由此計算出本文研究區(qū)的形狀、大小，方向相似度，見表3：

如此，很容易得到A1，B17兩圖元之間的形狀相似程度SimF（A1，B17）、A1，B17之間的大小相似程度SimS（A1，B17）和它們之間的方向相似程度Sim？茲（A，B）。結合層次分析模型，分別對空間幾何關系中的形狀、大小和方向相似度賦予不同的權重因子，即得到兩空間圖元的幾何度SimG（A，B）：

simG（A，B）=kF×simF（A，B）+kS×simS（A，B）

+k？茲×sim？茲（A，B）? （2）

其中，式（2）中的KS、K？茲、KF分別代表空間圖元幾何特征的大小，方向和形狀被賦予的比重因子。它們的和為1，且每個值的大小都在0到1的范圍內。

因為一個群組中有多個圖元，考慮到單圖元的相似性、整體的幾何相似性，本文采用均值的方法，見表4。

4.2 空間場景空間關系相似性的計算

空間關系是研究GIS重要理論之一，目前國內外學者一般從空間圖元間的拓撲關系、距離關系、方向關系等方面來度量空間關系的相似性[26，27]。

4.2.1 拓撲關系

本文數(shù)據(jù)匹配場景中只涉及面與面的相鄰及面與面的相離這兩種空間拓撲關系，研究群組的空間關系時，以群組為單位分析其內部圖元間的空間關系。

通過粗匹配的匹配結果排序，排除SimT（A（），B（））=0的情況。因此以下實驗只需考慮匹配場景與數(shù)據(jù)庫中待匹配場景的第二種情況。但是針對匹配場景有4個圖元目標，首先要選取其中一個單圖元為參考目標，從而以它為參考點來計算最短距離。本實驗是以A1，B1，B5，B9，B13，B17為參考目標得到的是群組整體的數(shù)據(jù)平均距離。計算拓撲相似度[26，27]可得表5。

4.2.2 方向關系

方向Voronoi圖模型和方向關系矩陣模型能夠通過數(shù)值來反映空間方向相似性。實驗考慮數(shù)據(jù)計算的復雜性和考慮圖元的整體性，選用改進的方向關系矩陣模型來描述空間方向相似度。在以A1，B1，B5，B9，B13，B17為參考目標時，根據(jù)方向關系[26，27]公式計算出匹配場景和數(shù)據(jù)庫待匹配各場景的特征向量。

在上述公式計算得到的空間圖元特征向量基礎上，根據(jù)相關系數(shù)法來度量兩個場景的空間關系相似度[26，27]SimD（AB，EF），見表6。

4.2.3 距離關系

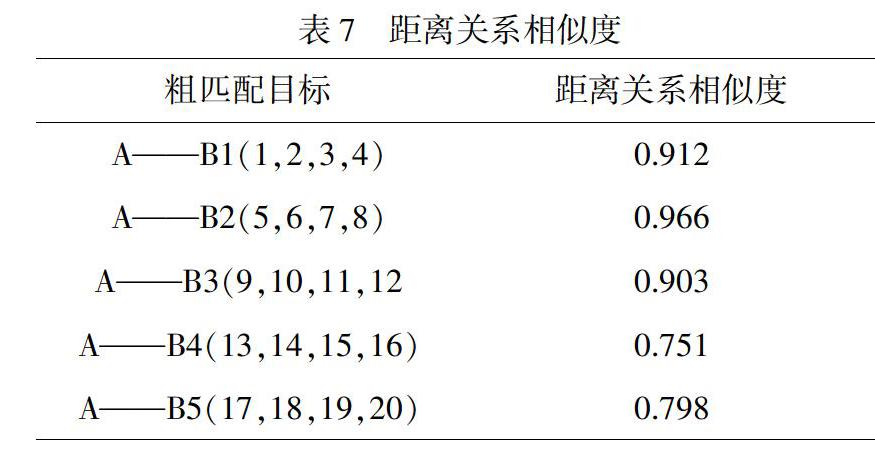
為了準確地計算距離關系的相似程度的大小，需選用圖元的重心點表示質心距離中的質心點。在粗匹配中第一步已經獲取各圖元的重心坐標。且粗匹配已經考慮了圖元的形狀、大小和方向的相似度，所以在計算空間場景A的距離關系[26，27]時，可以用每個圖元與參考圖元的距離總和作為匹配場景和數(shù)據(jù)庫待匹配各場景的距離（見表7）;

4.3 空間場景相似性的計算

為了提高匹配的準確性和充分利用匹配的約束特征，采用層次分析法同時度量空間幾何關系和空間關系，并賦予不同的權重因子。

本文參考文獻[22]的權重賦值如下：

SIM=0.8×[0.6×[0.4×simT+（simd+simD）×0.3]

+0.4×（simF+simS+sim？茲）]+0.2×simCU? （3）

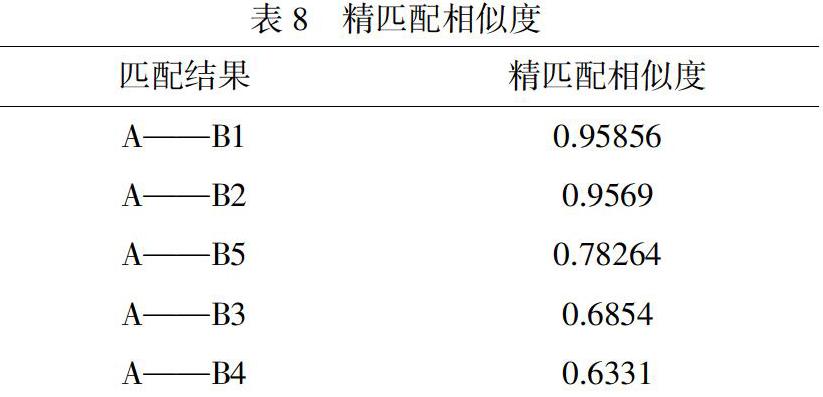
匹配結果排序，見表8。

5 總結

早就有“一圖勝千言”的說法，人們可以簡單便捷地通過感知將大量的數(shù)據(jù)融合用草圖表示出來，通過對草圖的分析，可以高效地整合信息，節(jié)約信息化成本和精確地獲取地理空間位置。由此可見草圖在描述空間場景方面的優(yōu)勢。

本文是以空間場景匹配為突破口，旨在解決在場景匹配中存在的場景旋轉問題。充分利用矢量數(shù)據(jù)的可視化及空間圖元間的空間幾何和空間關系特征。從人們對空間的定性思考的思維方式來說，空間場景匹配可以通過空間相似性進行度量。通過對空間相似性的研究，也為多源數(shù)據(jù)的融合和空間場景查詢提供了強有力的理論基礎，對將來智能化GIS的發(fā)展也有深遠的影響。

論文通過在前人相關知識研究的基礎上，進行了圖像場景匹配的分析列舉與匯總。從空間場景的中圖元的幾何特征（形狀、大小等）來計算圖元的幾何特征相似度，并對拓撲關系、方向關系、距離關系進行了深度的描述，并最終找出最合適的方法來度量空間關系的相似性;對提出的位置圖方法也進行了深度的解讀，清晰地表述粗匹配的各步驟及計算波形圖的相似度算法的介紹。最后取鄭州市某局部地區(qū)的矢量數(shù)據(jù)為實驗數(shù)據(jù)，對上述的方法進行了驗證，并對實驗的結果進行了多角度的分析評價。最終從實驗結果發(fā)現(xiàn)，基于空間相似性和旋轉不變性的方法能夠匹配到更為相似的空間場景，匹配的結果也更符合用戶的空間認知觀念。

——————————

參考文獻：

〔1〕潘柔.矢量面狀地物的空間場景相似性計算方法研究[D].長安大學，2015.

〔2〕Xu Y ， Xie Z ， Chen Z ， et al. Shape similarity measurement model for holed polygons based on position graphs and Fourier? descriptors[J]. International Journal of Geographical Information Science， 2017， 31（1-2）：253-279.

〔3〕郝燕玲，唐文靜，趙玉新，等.基于空間相似性的面實體匹配算法研究[J].測繪學報，2008，37（04）：501-506.

〔4〕鄭宇志，張青年.基于拓撲及空間相似性的面實體匹配方法研究[J].測繪科學技術學報，2013，30（05）：106-111.

〔5〕翟仁健.基于全局一致性評價的多尺度矢量空間數(shù)據(jù)匹配方法研究[D].解放軍信息工程大學，2011.

〔6〕趙彬彬.多尺度矢量地圖空間目標匹配方法及其應用研究[D].中南大學，2011.

〔7〕郭黎，鄭海鷹，王豪.面狀矢量空間數(shù)據(jù)匹配技術研究[J].海洋測繪，2009，29（03）：12-15.

〔8〕黃智深，錢海忠，王驍，金永崗，張強.基于降維技術的面狀居民地匹配方法[J].測繪科學技術學報，2012，29（01）：103-109.

〔9〕Zhang J R， Zhang J， Lok T M， et al. A hybrid particle swarm optimization-back-propagation algorithm for feedforward neural network training[J]. Applied Mathematics & Computation， 2007， 185（02）：1026-1037.

〔10〕Papadias D， Egenhofer M J， Sharma J. Hierarchical reasoning about direction relations? in： Proc. 4th ACM Workshop on GIS [C]. 1996：105-112.

〔11〕Papadias D， Delis V. Relation-based similarity[C]. Fifth ACM International Workshop on Advances in Geographic Information Systems. ACM， 1997：1-4.

〔12〕Ai T， van Oosterom P. A displacement method based on field analysis[C].In：SymPosium on Integrated Systems for Spatial Data Production，Custodian and Decision Support. Xi'an，2002：1-8.

〔13〕WANG Zeshen， DanLee. Buliding Simplification Based on Pattern Recognition and Shape Analysis[C].SDH 2000-Conference? Proceedings.2000，58-72.

〔14〕張橋平，李德仁，龔健雅.城市地圖數(shù)據(jù)庫面實體匹配技術[J].遙感學報，2004，8（02）：107-112.

〔15〕郭黎，崔鐵軍，鄭海鷹.基于空間方向相似性的面狀矢量空間數(shù)據(jù)匹配算法[J].測繪科學技術學報，2008，25（05）：115-121.

〔16〕Nedas K A， Egenhofer M J. Spatial-Scene Similarity Queries[J]. Transactions in Gis， 2008， 12（6）：661-681.

〔17〕Jun Chen， Chengming Li， Zhilin Li， et al. A Voronoi-based 9-intersection model for spatial relations[J]. International Journal of Geographical Information Science， 2001， 15（3）：201-220.

〔18〕童小華，鄧愫愫，史文中.基于概率的地圖實體匹配方法[J].測繪學報，2007，36（02）：210-217.

〔19〕邵世維.基于幾何特征的多尺度矢量面狀實體匹配方法研究與應用[D].武漢大學，2011.

〔20〕Rylov M A， Reimer A W. Improving label placement quality by considering basemap detail with a raster-based approach[J]. GeoInformatica， 2015， 19（3）：463-486.

〔21〕章莉萍，郭慶勝，等.相鄰比例尺地形圖之間居民地要素匹配方法研究[J].武漢大學學報信息科學版，2008，33（06）：255-260.

〔22〕劉濤，閆浩文.空間面群目標幾何相似度計算模型[J].地理信息科學學報，2013，15（05）：356-361.

〔23〕吳靜，尹濤.多尺度空間關系相似性研究[J].測繪科學，2011，36（04）：59-63.

〔24〕Deng M， Li Z L，Chen X Y. Extended? Hausdorff distance for spatial objects in GIS[J].International Journal of Geographical Information Science，2007，21（04）：459-475.

〔25〕艾廷華，帥赟，李精忠.基于形狀相似性識別的空間匹配[J].測繪學報，2009，38（04）：306-310.

〔26〕Frontiera， P.， R. Larson and J. Radke， A comparison of geometric approaches to assessing spatial similarity for GIR[J]. International Journal of Geographical Information Science， 2008. 22（03）： p. 337-360.

〔27〕Yan H，Chu Y，Li Z，et al.A quantitative description model for directional relations based on direction groups[J].Geoinformatica，2006，10（02）：177-195.