基于FNN-GARCH組合模型的船舶電磁儀表器材消耗預測研究
吳雯雯


[摘? ? 要] 針對船舶電磁儀表器材消耗預測過程中存在的數據序列波動性問題,結合電磁儀表器材消耗特點和維修保障工作實際,分別建立了模糊神經網絡模型(FNN)和廣義自回歸條件異方差模型(GARCH)以及FNN-GARCH組合模型,通過比較研究,基于FNN-GARCH1組合模型來對電磁儀表器材消耗量進行預測,可以很好地提高預測精度,為電磁儀表器材維修保障決策提供了定量依據和實用預測方法。
[關鍵詞] FNN模型;GARCH模型;FNN-GARCH組合模型;消耗預測;船舶電磁儀表;器材
doi : 10 . 3969 / j . issn . 1673 - 0194 . 2020. 15. 056
[中圖分類號] F224? ? [文獻標識碼]? A? ? ? [文章編號]? 1673 - 0194(2020)15- 0130- 02
0? ? ? 前? ? 言
在船舶設備器材中,電磁儀表器材占有很大的比重。隨著時間的推移,電磁儀表會因儲存壽命周期、儀表故障率、使用人員操作技能、使用強度、任務變化、裝備更替、管理水平以及海上水文氣象條件等因素的影響,出現電磁儀表器材消耗的情況。由于舊的或者需要維修的電磁儀表器材在被更換或維修之后,會出現新舊儀表與維修后的儀表同時工作的情況,因此,電磁儀表器材的消耗規律十分復雜,而其消耗規律又會直接影響維修保障過程中電磁儀表器材備品備件的庫存決策。可見,尋求一種能夠有效預測電磁儀表器材消耗量的方法是十分必要的。
1? ? ? 樣本數據獲取
為了研究船舶電磁儀表器材的消耗規律,這里選取了2017年至2019年某船舶電磁儀表器材消耗的實際數據,如表1所示。
2? ? ? 組合模型的建模步驟
(1)依據電磁類消耗量時間序列建立ARMA模型,以消除數據線性部分的影響。(2)檢驗殘差的異方差性。如果消耗量序列具有無異方差性,則選擇ARMA模型;如果有異方差性,則建立異方差模型。(3)驗證序列的ARCH效應。如果具有ARCH效應,
則建立GARCH模型,消除不顯著的變量。(4)修正或改進GARCH模型,如果模型能夠實現對電磁類儀表器材消耗量的準確預測,則選擇GARCH模型。(5)選擇模糊神經網絡模型FNN與GARCH模型組合,建立組合預測模型[1]。
3? ? ? ARMA模型的建立
3.1? ?消耗量數據序列的ADF檢驗
設定檢驗的顯著性水平為α=0.05,則消耗量數據序列{xt}的單位根ADF檢驗結果,如表2所示。
在進行單位根檢驗時,假定原來的假設為:H0:消耗量數據序列中存在一個單位根,由于Prob.為:0.138 7>0.05,因此,接受原來的假設,即消耗量數據序列是不平穩的。進行一階差分處理后,對新序列進行單位根檢驗,結果如表3所示。
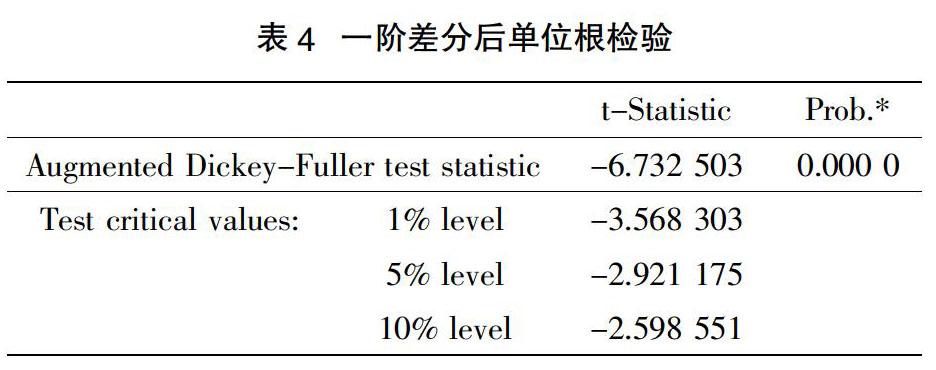
由表3可知,Prob.=0.000 1<0.05,因此,可以拒絕原來的假設,即一階差分后的消耗量數據序列是平穩的[2]。將一階差分后的數據序列再進行單位根檢驗,結果如表4所示。
3.2? ?消耗量序列的峰度與偏度
消耗量序列峰度與偏度檢驗結果為:Mean:26.992 57;Median:22.053 81;Maximum:94.511 42;Minimum:1.454 689;Std.Dev:21.248 29;Skewness:1.246 123;Kurtosis:4.030 381;Jarque-bera:18.182 44;Probability:0.000 113。由此可見,峰度大于3,偏度大于0,這表明該序列具有明顯的尖峰性,與正態分布相比是右偏的。Jarque-bera值為:18.18 244>0,Prob.=0.000 113,說明消耗量序列不服從正態分布,具有明顯的非線性特征。
3.3? ?消耗量的ARMA預測模型
對消耗量序列殘差進行白噪聲檢驗可知,每一階的滯后項p>0.05,自相關和偏相關值基本在邊界線以內,說明可以建立ARMA模型進行預測。由于是序列基本平穩的,因此,可得模型:Y=0.272 48×Y(-1)+0.491 73×Y(-2)+0.804 36
4? ? ?GARCH模型的建立
GARCH模型運用過去的方差及其預測值來構建未來方差的自回歸條件異方差時間序列模型。GARCH效應,一是指異方差性,即隨著時間的變化方差也會相應地發生變化;二是條件性,即預測值與過去的相鄰觀測值有關,相鄰觀測值的個數會隨著階數的增加而同步增加。
4.1? ?異方差性與ARCH效應檢驗
設隨機干擾項εt~ARCH(q),則ht=α0+α1εt-1+…+αt-q。為檢驗該序列是否存在ARCH效應,可做原假設:H0:α1=α2=…=αq=0,H1:?堝αi≠0(1≤i≤q)。對殘差序列進行ARCH效應檢驗:Prob.F(1,57):0.0095;Prob.Chi-Square(1):0.0101。由此可見,P值均小于0.05,因此,殘差序列是相關的且具有異方差性,存在ARCH效應,可以運用GARCH類模型進行建模預測。
4.2? ? GARCH模型
GARCH模型是在自回歸條件異方差模型ARCH基礎上發展而來的,ARCH模型比較適用于短期自相關系數的問題,對于長期的自相關問題則需要通過增加移動平均階數來對模型進行改進,構建GARCH模型,以提升對器材消耗量的預測精度。
5? ? ? 組合模型的建立
5.1? ?組合模型的建模步驟
組合模型的建立步驟:一是建立電磁類儀表器材消耗量數據序列{xt,t=1,2,…,n}時間序列模型xt的線性部分;二是建立GARCH模型對隨機干擾項進行預測,對非線性部分運用FNN模型建模預測。
將60個數據中的48個數據作為訓練樣本,其余的12個數據作為測試樣本。為了提升預測精度,對原始數據序列做以下變換:
Yt=log(Xt),t=1,2,…,60。
5.2? ?組合模型的建立過程
建立兩種混合模型FNN-1和FNN-2,其中:FNN-GARCH1模型:■t=f(■t,■t)
FNN-GARCH2模型:■t=f(■t)
其中,■t為GARCH模型的預測值,■t為異方差預測值。
5.3? ?變換后殘差序列的ARCH效應檢驗
變換后殘差序列的ARCH效應檢驗結果為:Prob.F(2,57):0.000 0;Prob.Chi-Square(2):0.000 0。由此可知,殘差序列存在ARCH效應。可以對消耗量數據序列滯后模型的殘差項建立GARCH(1,1)模型并對參數進行估計,估計結果如表5所示。
由此可得出模型:Yt=3.140 256Yt-1+εt
GARCH=0.003 01-0.174 27×RESID(-1)2+1.064 61×GARCH(-1)
6? ? ? 模型比較分析
采用2017年至2019年的電磁儀表器材消耗數據進行擬合,求出各種模型的擬合結果并分別計算出各個模型的平均絕對誤差(MAE)值、平均絕對百分比誤差值(MAPE)以及均方百分比誤差(RMSE)值,如表6所示。通過比較各個誤差值的大小,選出三個誤差值都最小的,作為電磁儀表器材消耗量估計的最優預測模型。
從表6中可知,FNN-GARCH1組合模型的MAE、MAPE、RMSE的值與其他模型相比都是最小的,因此,FNN-GARCH1組合模型能夠較為準確地預測船舶裝備電磁類儀表器材消耗量情況。
7? ? ? 結? ? 論
電磁儀表器材是保障機電設備正常工作的關鍵部件之一,做好船舶電磁儀表器材消耗的預測工作是維修保障決策的重要環節。將FNN模型與GARCH模型相結合,建立FNN-GARCH1組合模型,可以克服采用單一方法預測的缺陷,提升電磁儀表器材消耗預測的準確性和可靠性,其預測值可以作為維修保障決策的定量依據。
主要參考文獻
[1]馬艷青.馬爾科夫轉換-GARCH模型的MCMC參數估計和方法研究[D].重慶:重慶大學,2015.
[2]李玉芳.波動率分析:GARCH族及模糊時間序列模型[D].杭州:浙江大學,2012.

