基于重置頂點下標的網絡最大流算法

羅甜甜，趙禮峰

(南京郵電大學 理學院，江蘇 南京 210023)

0 引 言

最大流問題是一種組合最優化問題，在許多實際的網絡系統中都存在著流量和最大流問題，例如鐵路運輸系統中的車輛流[1-3]、城市排水系統中的水流問題[4-6]、控制系統中的信息流問題等[7-9]都可以抽象出最大流模型，從而轉化為最大流問題。所以最大流問題應用廣泛，實踐性強。求解網絡最大流的常用算法可以分為增廣路徑算法和預流推進算法[10]。其中后者的編碼程度過高，因而前者為經常使用的算法。而屬于增廣路徑算法的主要有：Ford-Fulkerson算法[11]，Edmonds-Karp算法和最短增廣鏈算法[12]，ISAP算法。設容量網絡D的頂點數為m，弧數為n，弧容量的最大值為cmax，Ford-Fulkerson算法的算法復雜度則為O(mncmax)，當容量網絡某些弧容量為無理數時，此算法便會陷入無限循環。Edmonds-Karp對其修正，用寬度優先取代了深度優先。最短增廣鏈算法是將頂點按照其與源點的最短距離分層，分層時用寬度優先法，而尋求增廣路徑時采用深度優先策略。兩者結合效率明顯高于Edmonds-Karp算法。ISAP算法是對最短增廣鏈算法的優化，即通過深度優先不斷修改距離標號的方式省去每一次的寬度優先。但由于最短增廣鏈算法在構建分層剩余網絡中選取增廣鏈仍然存在隨機性使得某些增廣鏈缺失，導致算法執行后的結果偏小，失去其準確性。

該文針對最短增廣鏈算法在分層剩余網絡后尋找增廣鏈不考慮先后順序使得最大流值偏小這一問題進行改進，沿用了最短增廣鏈算法通過寬度優先將頂點分層的思想，將頂點根據層數，源弧容量，匯弧容量和頂點容差這四個因素來確定頂點被選擇的先后順序。然后根據相應規則來選取增廣鏈，此規則可以保證最短增廣鏈優先選取，并可以井然有序地快速找出所有增廣鏈。

1 基本概念

定義1[13]：容量網絡D=(V,A,c)，其中V表示D中頂點的集合，A為D中弧的集合，c表示弧上的容量。

定義2[13]：流量。設f是容量網絡D中弧集A上的一個實函數，?a=(vi,vj)∈A，記f(a)=fij。如果函數f={fij|(vi,vj)∈A}滿足守恒條件：

則稱f是D的一個流，此時，fij稱為通過弧(vi,vj)上的流量。

定義3[13]：頂點層數：在容量網絡D中，用寬度優先搜索[14-15]找出從源點vs到任意一點vi(vi∈V)的最短路的長度hi稱為頂點vi的層數，即由vs到vi的路徑中所含的最少弧數。(第零層只有一個節點就是源點即hs=0)。

定義4[16]：剩余網絡D(f)=(V,A(f),cf),其中V表示容量網絡D中頂點的集合，f為D上的可行流，A(f)是D(f)上弧的集合，其中，

A(f)=A+(f)∪A-(f)

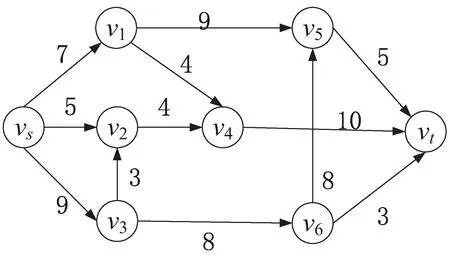
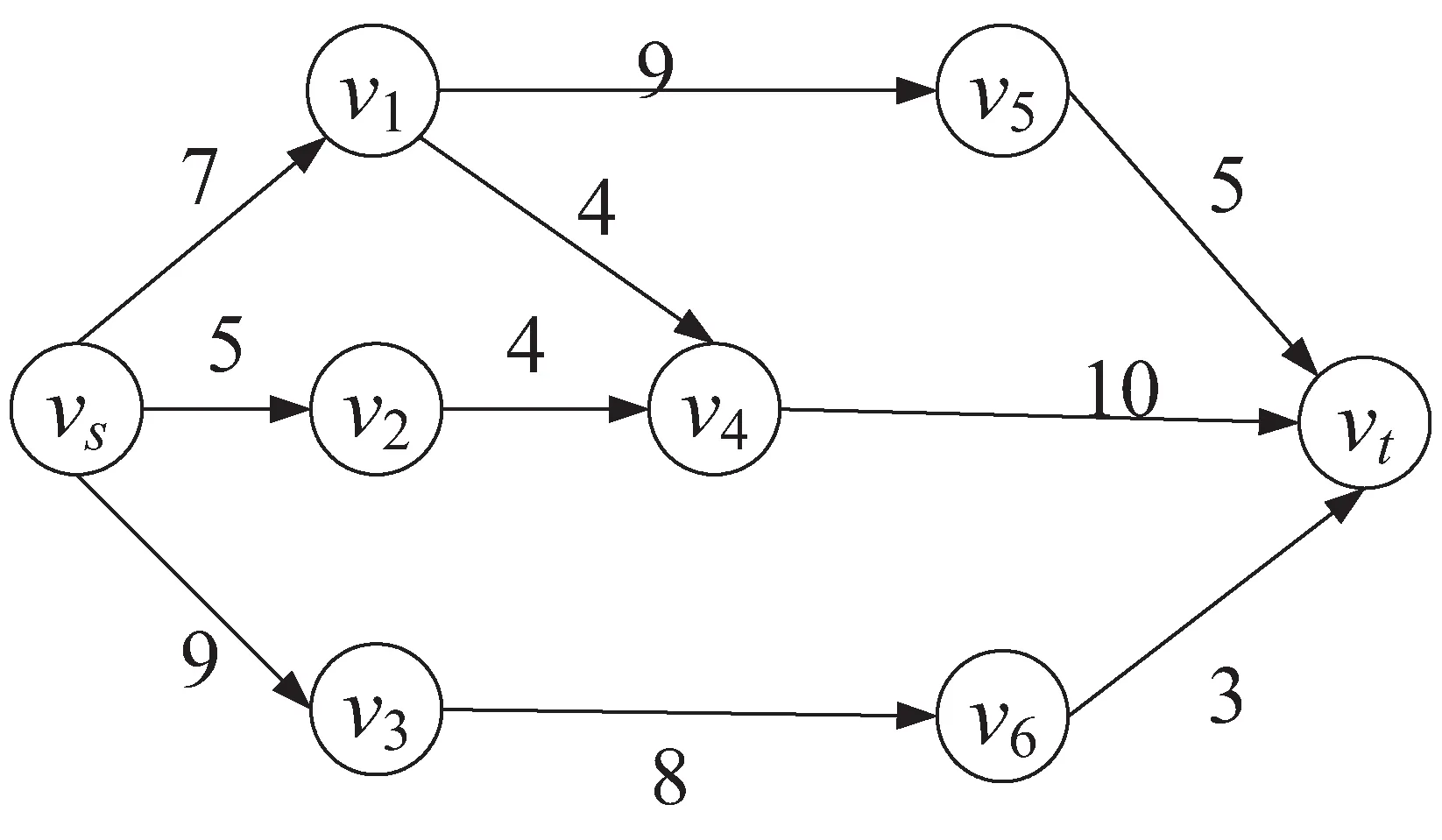
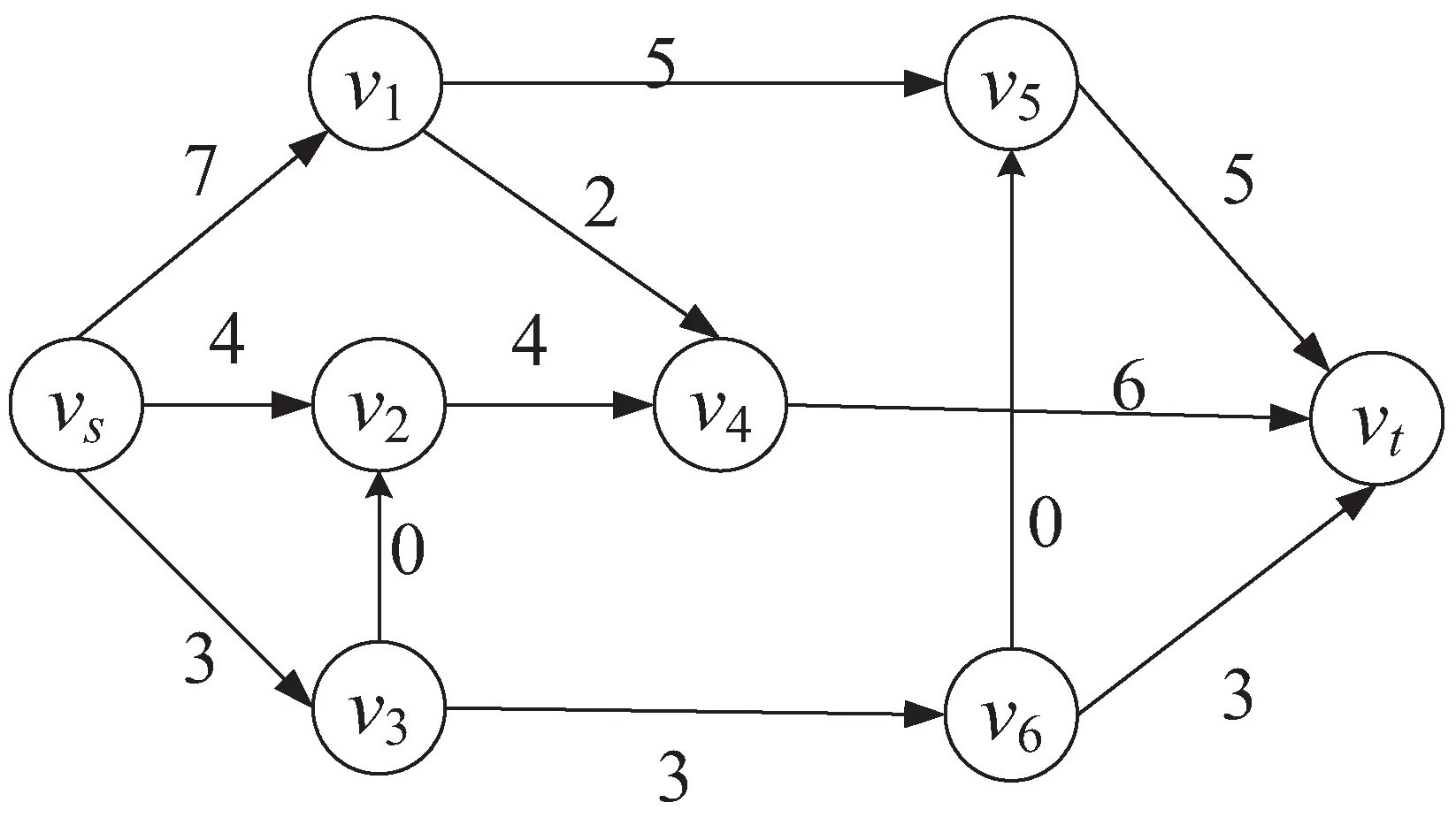
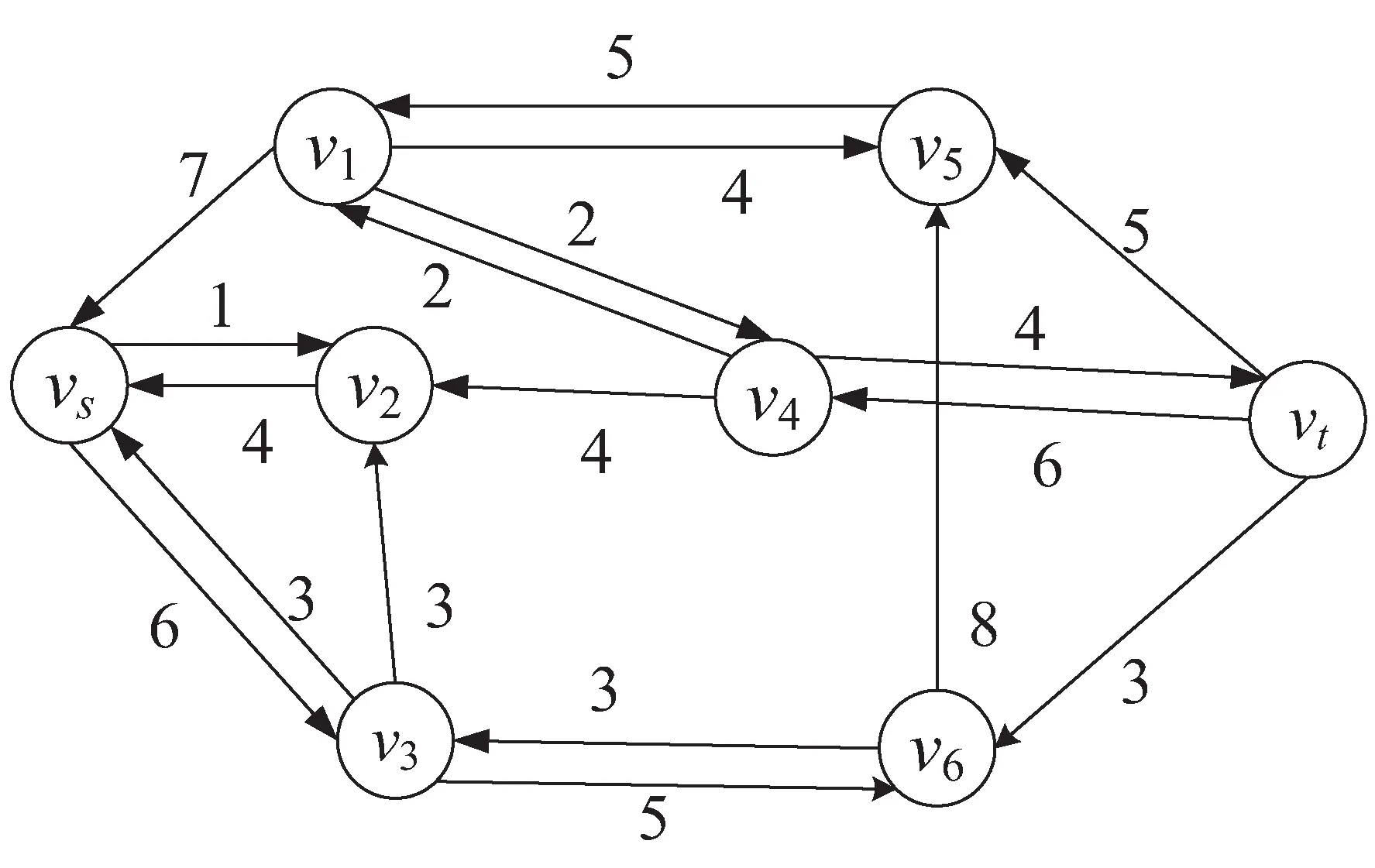
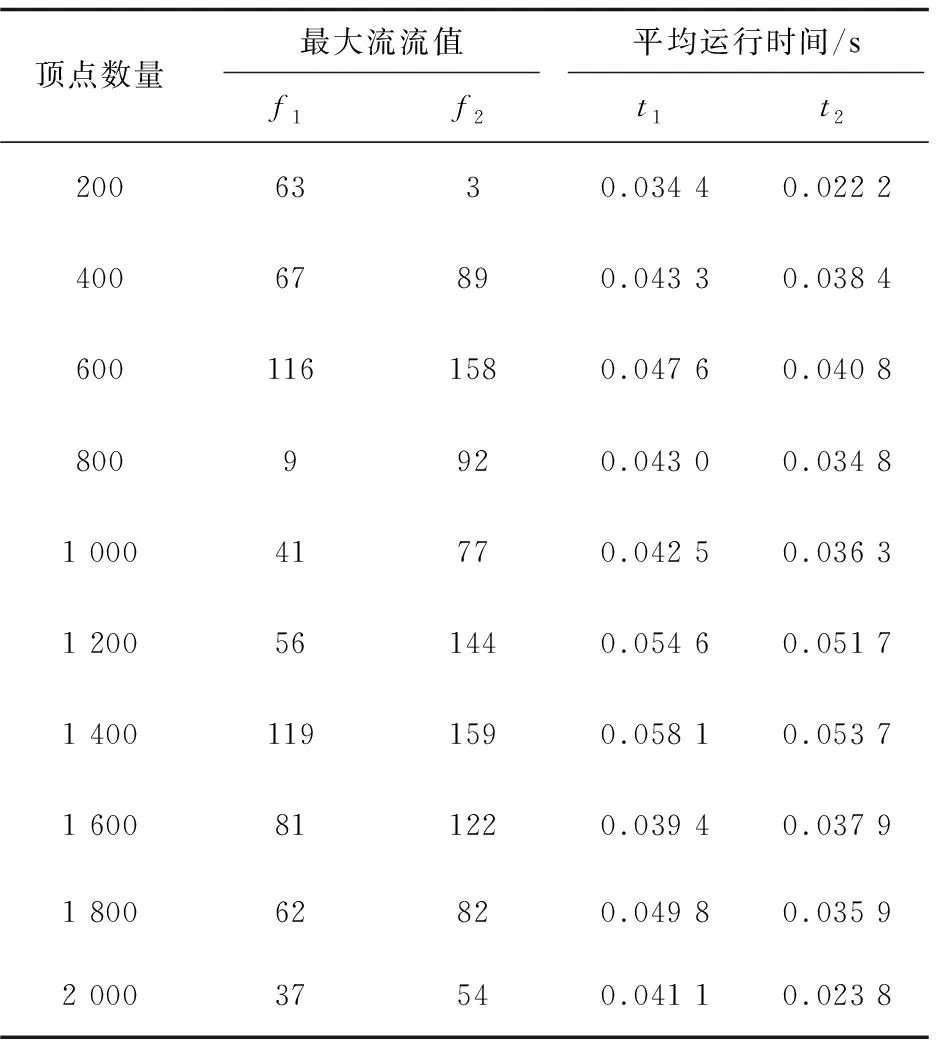
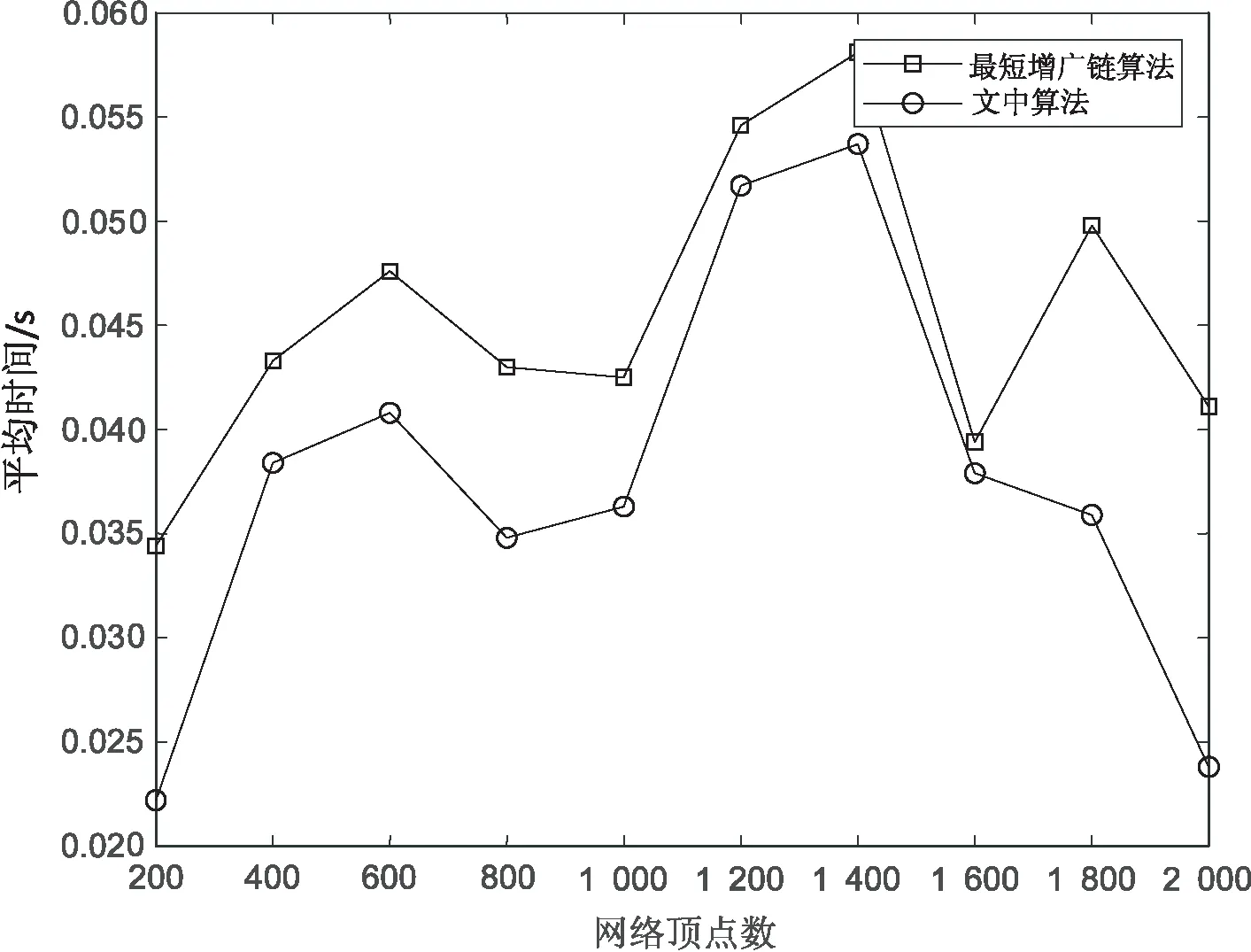
A+(f)={(vi,vj)|(vi,vj)∈A,fij

A-(f)={(vi,vj)|(vj,vi)∈A,fij>0}

cij(f)為(vi,vj)關于f的剩余容量，其中，

定義5[16]：分層剩余網絡記為AD(f)=(V'(f),A'(f),cf)，其中，

V'(f)={vt}∪{vi∈V|h(vi)

A'(f)={(vi,vj)∈A(f)|h(vj)=h(vi)+

1

∪{(vi,vt)∈A(f)|h(vi)=h(vt)-1}

定義6：源弧容量：由源點vs到頂點vi(vi∈V)所構成的弧的容量c(vs,vi)，記為αi。

定義7：匯弧容量：由頂點vi(vi∈V)到匯點vt所構成的弧的容量c(vi,vt)，記為βi。

定義8：頂點容差：頂點vi(vi∈V)的所有出弧容量減去該頂點的所有入弧容量的值為頂點vi(vi∈V)的容差，記為γi。

定義9：中間頂點(除源點、匯點外)標號過程：對于頂點vi，當hi=1時，求出αi和γi，將其標號為(1,αi,γi)；當1

定義10：重置頂點下標規則：已知網絡D，其頂點數為n，則將源點vs重置為v1，匯點vt重置為vn。除源點匯點外，中間頂點的重置標號依次為v2,v3,…,vn-1。首先按照頂點層數hi由低至高的順序依次由小到大編號重置；當hi相等時，分三種情況考慮：

(1)hi=1，按照源弧容量αi由低至高的順序依次由小到大編號重置，當αi相等時，再按照容差γi由低至高的順序依次由小到大編號重置；

(2)當最高層的頂點唯一，且13)時，當最高層頂點不唯一，且13)時，都按照容差γi由低至高的順序依次由小到大編號重置；

(3)當最高層的頂點唯一，且hi=ht-1時，或者當最高層的頂點不唯一，且hi=ht時，都按照匯弧容量βi由低至高的順序依次由小到大編號重置，當βi相等時，再按照容差γi由低至高的順序依次由小到大編號重置。

定理：設f是容量網絡D中的可行流，則f是D的最大流當且僅當D中不存在f增廣鏈。

2 新算法思想及步驟

2.1 算法思想

求網絡最大流[17]的基本思想是根據定理1，即從容量網絡D中的一個可行流出發，尋找增廣鏈進行增廣，直至D中不存在增廣鏈為止。根據此思路，目的是尋找增廣鏈，關鍵是確定選取增廣鏈的先后順序。首先是根據一定規則對頂點下標進行重置，形成與原網絡D相對應的新網絡D1。然后按照優先選取頂點標號值較大的增廣鏈增廣的原則在D1中尋找增廣鏈，直至不存在從源點到匯點的增廣鏈即可結束該算法。

2.2 算法步驟

Step1:利用寬度優先搜索求出原容量網絡D中各個頂點的層數，再根據定義9對中間頂點進行標號。

Step2：根據定義10對頂點下標進行重置，形成對應的新網絡D1。

Step3：初始化新網絡D1，令D1中每條弧的流量為0。

Step4：從頂點v1出發，判斷D1中是否存在一條從v1到vn(n為網絡D1的頂點個數)的增廣鏈，若存在轉Step5，否則轉Step7。

Step5：從頂點v1出發，沿著與其關聯弧所在頂點下標值較大的原則找一條從v1到vn的增廣鏈，若存在轉Step6，否則轉Step7。

Step6：調整，求該鏈上各弧容量的最小值δ，并將此增廣鏈中對應弧的容量后面標上δ，其中δ=min{cij-fij}。在飽和弧上標上終止弧標志“||”，增廣后轉Step4。

Step7：計算所有以v1為發點的弧的流量和，得到最大流值v(f)，算法結束。

3 新算法可行性與復雜度分析

3.1 可行性分析

新算法的主要思想是沿著所規定好的原則尋找增廣路徑，每次增廣至少使一條弧達到飽和。假設網絡D中共有m條弧，那么最多通過m次增廣后，網絡D中就不存在從源點到匯點的增廣鏈，即算法結束。說明算法經過有限次步驟就會終止，不會陷入無限循環。

3.2 復雜度分析

新算法主要分為兩個過程：一是標記、比較和編號過程，通過這些準備工作構建新網絡流圖；二是增廣過程，沿著頂點下標值大的原則尋找增廣鏈。設容量網絡D的頂點數為n，弧數為m。該算法執行時，第一個過程屬于準備過程只執行一次，而執行一次準備工作的計算量分別是：(1)計算層數O(n)次；(2)計算容差最多需要O((n-2)m)次；(3)比較大小重新編號最多需要O(2nlog2n)次。第二個過程最多執行O(m)次，于是該算法的時間復雜度為：

O(n)+O((n-2)m)+O(2nlog2n)+O(m)=O(2nlog2n+nm)

4 應用實例

例：求出圖1的容量網絡D中從源點vs到匯點vt的網絡最大流。

圖1 容量網絡D

解：方法一(文中算法)：

(1)首先根據寬度優先搜索求出各頂點層數，得：

(2)對于hi=1，要求出αi和γi，于是可得：

因為ht=3<4，對于1

(3)由(2)所得數據對頂點標號，如圖2所示。

圖2 標號后的容量網絡D

(4)再根據定義8重置頂點下標：令

重新構造容量網絡D1，如圖3所示。

圖3 容量網絡D1

(5)在D1中按照優先選取頂點下標值較大的原則尋找增廣鏈：

增廣后的網絡流圖如圖4所示。

圖4 可行流f

在圖4中找不到v1到v8的增廣鏈了，故圖4即為最大流f，計算最大流值為V(f)=4+3+3+5+1=16。

方法二(最短增廣鏈算法)：

(1)在D中取f1為初始可行流，令f1為零流。然后構建分層剩余網絡AD(f1)，見圖5。

圖5 分層剩余網絡AD(f1)

(2)在圖5中找增廣鏈，找到了如下幾條增廣鏈：

增廣之后，得到可行流f2，見圖6。

圖6 可行流f2

(3)繼續構建剩余網絡D(f2)，見圖7。發現D(f2)中不存在(vs,vt)路，算法結束。f2即為容量網絡D的最大流，在圖6中計算與源點關聯的所有弧的流量和為14，即最大流的流值為14。可見與方法一相比流值偏小。

圖7 剩余網絡D(f2)

5 算法的仿真與比較

5.1 實驗環境與設計

該算法使用的實驗仿真平臺是MATLAB2016a，處理器為Intel(R) Core(TM) i3-4030U CPU @1.90 GHz，內存4 GB，Windows7版本64位操作系統。

仿真實驗采用的是BA無標度隨機網絡，并將網絡規模的頂點數依次設為200，400，600，800，1 000，1 200，1 400，1 600，1 800，2 000。然后在給定的網絡規模下，對新算法和最短增廣鏈算法進行10次仿真實驗。其中參數f1和t1分別表示最短增廣鏈算法的最大流值和它的運行時間的平均值，參數f2和t2分別表示新算法的最大流值和其運行時間的平均值。

5.2 實驗結果統計與分析

根據表1的內容可以看到兩種算法在不同的網絡規模下得出的最大流值情況以及算法的平均運行時間。明顯可以得出新算法比最短增廣鏈算法的結果更精準。由圖8可以看到新算法的運行時間較短。

表1 新算法與最短增廣鏈算法在不同網絡規模的運行數據

圖8 新算法與最短增廣鏈算法的平均運行時間

6 結束語

文中針對最短增廣鏈算法在構建分層剩余網絡后選取增廣鏈增廣的先后順序不當而影響最大流值偏小的問題進行了改進處理。首先對頂點標號根據其在整個網絡圖所處位置按一定規律重新編號，為后面尋找增廣鏈有規可循且節約了時間，也使得網絡圖更加清晰直觀。通過很多實例和實驗仿真證實了算法的準確性和高效性。