考慮柔輪杯體變形的諧波傳動空間共軛齒廓設計與分析

朱飛鴻1，杜雪松1，宋朝省1，朱才朝1，楊勇，廖德林

(1.重慶大學機械傳動國家重點實驗室，重慶，400044；2.深圳市大族精密傳動科技有限公司，廣東深圳，518057)

諧波齒輪傳動具有結構緊湊、減速比大、傳動精度高等優點，廣泛應用于航空航天、衛星通信和工業機器人等領域。在諧波傳動中，柔輪發生的彈性錐度變形具有空間特征，尤其是工業機器人所使用的短筒諧波減速器將具有更明顯的空間變形，因此，要獲得良好的嚙合特性，剛輪與柔輪需按空間共軛齒廓進行設計。目前的諧波傳動齒形設計多以平面共軛齒形代替空間齒廓，或者雖然進行了空間齒廓設計但采用了較多假設，這樣設計的齒形將會導致較多的嚙合干涉和尖點嚙合，從而產生不利于傳動的齒面磨損，因此，有必要基于柔輪空間錐度變形建立更精確的諧波傳動運動學模型，開展柔輪空間共軛齒廓設計研究。國內外學者對諧波傳動結構設計分析[1-5]、嚙合理論及運動學[6-7]、齒形研究[8-10]，側隙及嚙合力分布[11-12]，動態性能和控制[13]等領域開展了大量研究。在諧波傳動共軛齒廓設計和求解方面，楊勇等[14]提出了精確的橢圓凸輪波發生器平面諧波傳動運動學方法，為零側隙諧波傳動平面共軛齒廓的求解提供了思路；DONG等[7]提出了考慮柔輪錐度變形的諧波傳動運動學模型，指出由于柔輪的空間變形，剛柔輪共軛齒廓之一必須是空間齒廓，否則會導致不必要的干涉和變形；吳偉國等[15-16]提出采用具有傾斜角度的剛輪齒形與產生空間錐度變形的柔輪嚙合，并通過實驗驗證該方法可提高諧波減速器的傳動剛度，但沒有考慮若剛輪采用空間齒廓在批量加工時的工藝性問題；劉鄧輝等[17]考慮柔輪錐度變形特征造成柔輪各截面中面曲線的差異，將剛輪空間齒廓的設計轉化為多個橫截面內的平面齒廓設計，該方法柔輪采用平面齒形，剛輪為空間共軛齒廓；周祥祥等[18-19]將柔輪齒圈離散成許多個橫截面，通過合理調節各截面柔輪齒廓的徑向位置設計具有傾角的柔輪空間齒廓；陳曉霞[20]基于直母線假定較準確地分析了柔輪空間錐度變形特征，但并未建立其運動學模型求解空間共軛齒廓。綜上所述，現有研究都將剛柔輪齒廓看成離散的一系列截面來設計共軛齒廓，部分學者考慮了柔輪錐度變形造成的各截面中面曲線的差異，但忽略了柔輪杯體的空間變形還會引起柔輪齒的空間轉動，變形后的柔輪齒橫截面將不再垂直于旋轉軸。本文作者考慮柔輪空間變形帶來的中面曲線變化和柔輪齒空間方位變化，建立更精確的諧波傳動運動學模型，利用數值法求解柔輪空間共軛齒廓，研究柔輪杯體空間變形所產生的空間轉角，以及該轉角對嚙合過程中的共軛區域、柔輪齒運動軌跡和齒面嚙合跡線帶來的特殊影響，以便為高精度諧波齒輪傳動共軛齒廓的求解和優化提供指導。

1 建立空間共軛運動學模型

諧波傳動中，柔輪變形取決于波發生器幾何形狀和柔輪受載狀況，柔輪受載狀況能顯著影響杯體變形，但剛柔輪齒間載荷分布又取決于輪齒齒形，如果要考慮載荷施加對柔輪變形帶來的影響，就要首先建立空載狀態下的輪齒幾何特征，然后加入載荷，分析其帶來的影響，以此作為齒形修形依據。故本文在理想輕載狀態下建立考慮柔輪殼體中面空間變形的運動學模型，主要假設如下[20]：

1)柔輪中面是柔輪圓柱殼體的中面；柔輪中面曲線是柔輪中面與橫截面的交線；

2)柔輪杯體看作鉸接在輸出端剛性杯底圓盤周邊的圓柱殼，柔輪齒看作剛體，隨直母線繞杯底鉸接點發生由徑向位移w和切向位移v引起的2個轉動；

3)柔輪杯體變形后，任意截面中面曲線由平面圓變為空間曲線，該曲線由徑向、切向和軸向位移確定，忽略軸向位移認為各中面曲線變形后仍在同一平面。

以剛輪固定、波發生器逆時針旋轉輸入、柔輪順時針旋轉輸出的諧波傳動為研究對象，考慮柔輪杯體變形，建立如圖1所示坐標系統，用于描述柔輪、剛輪和波發生器之間的相對運動及柔輪中面上選定點的位移和空間轉角。其中，以剛輪回轉中心O2為原點建立剛輪固定坐標系S2{OX2Y2Z2}。以波發生器回轉中心O為原點建立波發生器動坐標系S{O-XYZ}，X軸為波發生器長軸。柔輪齒動坐標系為S1{O1-X1Y1Z1}，X1軸為柔輪輪齒對稱線，原點為X1軸與柔輪中性層交點。為準確描述柔輪在波發生器作用下的空間變形特征，建立輔助坐標系Sa，Sb和Sc來描述變形過程中切向位移v、徑向位移w以及法向轉角μ帶來的坐標軸方位變化。在初始位置，X1，X2和X三軸共線，坐標系S和S2重合，坐標系S1中O1點位于波發生器長軸頂點。圖1中所示位置為波發生器相對于X2軸逆時針旋轉φ2時，柔輪非變形端相對于X2軸順時針旋轉α，而變形端則順時針旋轉γ。圖1中，φ為波發生器相對于柔輪輸出端的轉角。

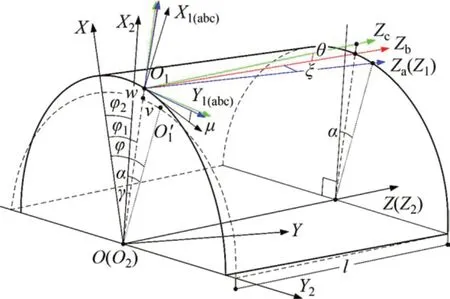
圖1 諧波傳動坐標系Fig.1 Coordinate systems of HD

波發生器迫使柔輪中面發生錐度變形，該變形過程中的位置移動及坐標軸方位變化由輔助坐標系Sa，Sb和Sc以及坐標系S1之間的平移和連續轉動來描述：1)柔輪變形使得嚙合端O1點產生徑向和切向位移從圖1中O1′處移動到O1處，對應輔助坐標系Sc，Xc軸沿OO1方向，Zc軸平行于波發生器旋轉軸Z軸(圖2(a))；2)由徑向位移w引起繞Yc軸的轉角θ，輔助坐標系Sc旋轉至坐標系Sb(圖2(b))；3)由切向位移v引起輔助坐標系Sb繞Xc軸的轉角ξ(Xc軸不是Sb坐標系的坐標軸)，輔助坐標系Sb旋轉至坐標系Sa(圖2(c))；4)由柔輪變形引起繞Za軸的轉角位移μ，輔助坐標系Sa旋轉至坐標系S1(圖2(d))。

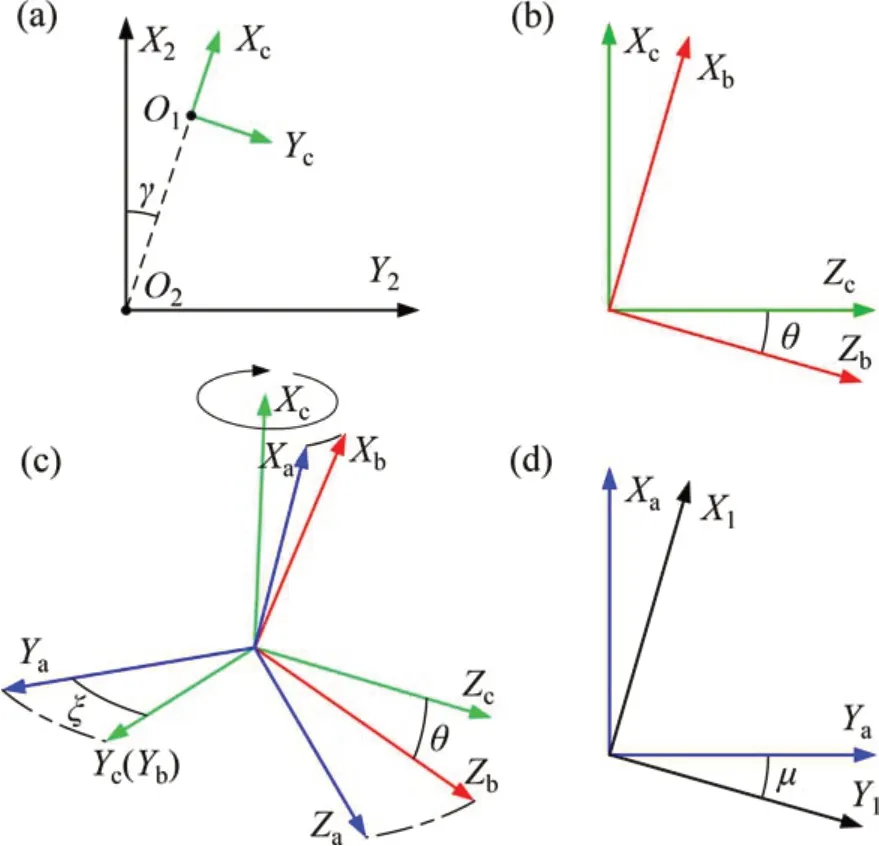
圖2 諧波傳動輔助坐標系Fig.2 Auxiliary coordinate systems of harmonic drive

為描述柔輪空間變形引起柔輪齒的方位變化，本文定義了由徑向位移w引起繞Yc軸的轉角θ和由切向位移v引起繞Xc軸的轉角ξ，這2 個空間轉角對柔輪齒空間方位變化進行描述。所有運動參數選擇以φ1為自變量表示，引入橢圓第二偏心率?，可以推出2個空間轉角的計算公式及其對φ1的求導表達式如下：

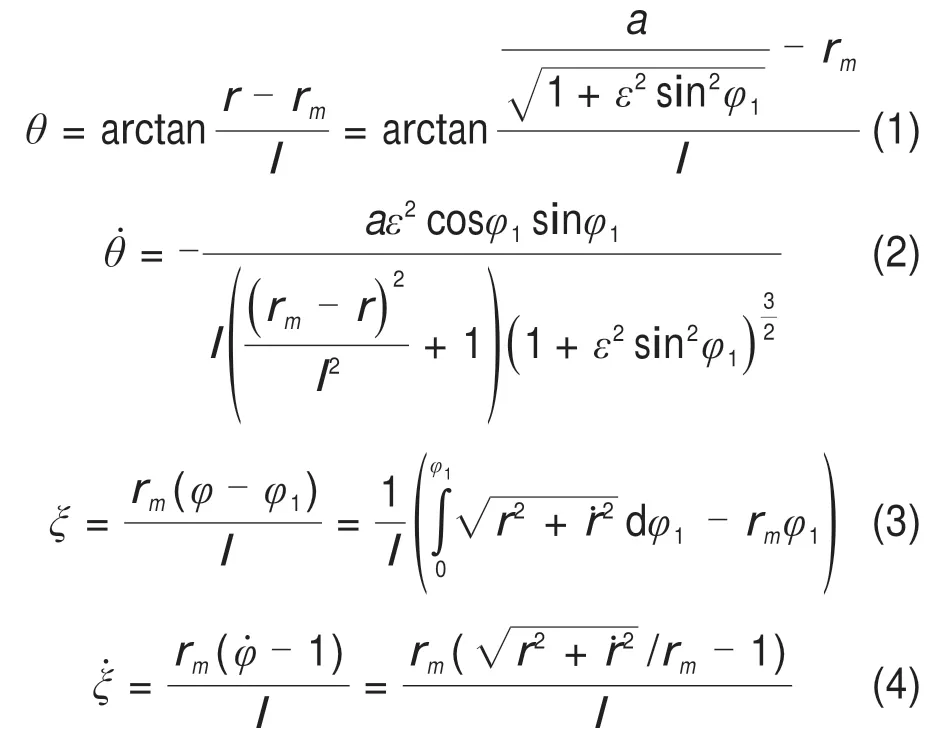
式中：rm為柔輪未變形時中性層半徑；ω為變形系數；l表示設計主截面至杯底距離；a為柔輪中性層橢圓長軸；b為柔輪中性層橢圓短軸；Zf為柔輪齒數；Zc為剛輪齒數。

上述各式中的極徑OO1長度r、轉角位移μ、波發生器相對于柔輪輸出端轉角φ、波發生器相對于剛輪轉角φ2和柔輪嚙合端旋轉角度γ的計算式及其對φ1的求導表達式參見文獻[14]。

2 求解共軛齒廓

圖1和圖2所示的坐標系S2到S1的坐標變換矩陣如下：

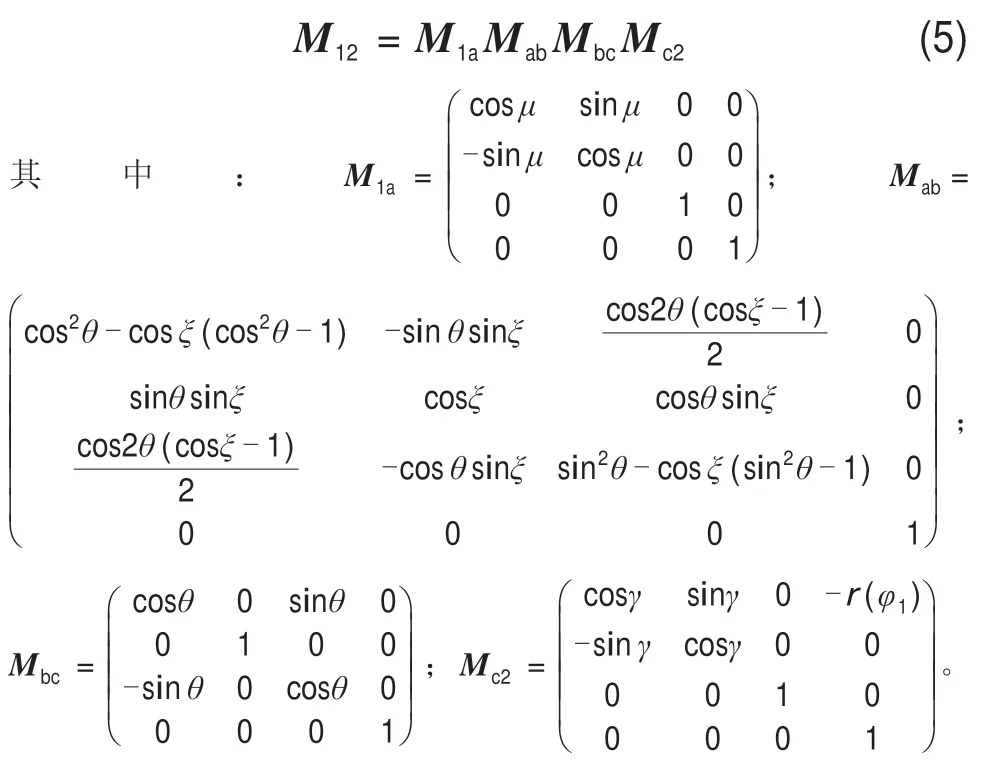
同理易得底矢變換矩陣W12。根據齒輪嚙合原理，兩齒面在接觸點處必須滿足以下嚙合方程：

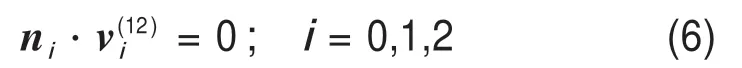
式中：ni為接觸點的單位公法矢；為接觸點的相對運動速度矢量。

在S1坐標系中考慮式(6)，代入n1=W12·n2和可將式(6)轉化為

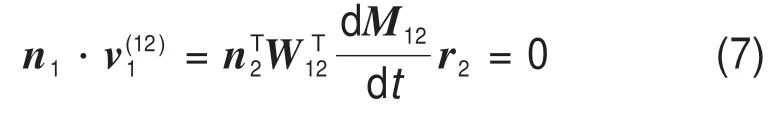
將剛輪齒廓曲線表示為以弧長s為參數的方程，對于齒廓曲線上每一點，都對應1個參數值si。將每一個弧長si(i=1，2，…，s)所對應齒廓曲線點的矢徑r2和法向量n2代入式(7)，得出該點發生共軛運動時的角φ1，記為φ1i(i=1，2，…，s)。根據每個φ1i確定對應M12中各元素值，得出相應的坐標變換矩陣M12i，代入下式，即可得出與剛輪齒廓共軛的柔輪理論齒廓。

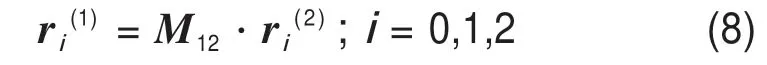
3 實例分析

以1款雙圓弧諧波減速器為例，波發生器為標準橢圓凸輪，剛輪輪齒坐標系和公切線式雙圓弧剛輪齒廓如圖3所示。該減速器柔輪齒數Zf=160，剛輪齒數Zc=162，模數m=0.4，齒寬B=12 mm，波發生器徑向變形系數ω0=1.0，全齒高h=1.7m=0.68 mm，齒頂高ha=0.8m=0.32 mm，齒根高hf=0.9m=0.36 mm，柔輪齒圈上齒形設計主截面至杯底的距離l=20 mm。剛輪具體參數如表1所示。

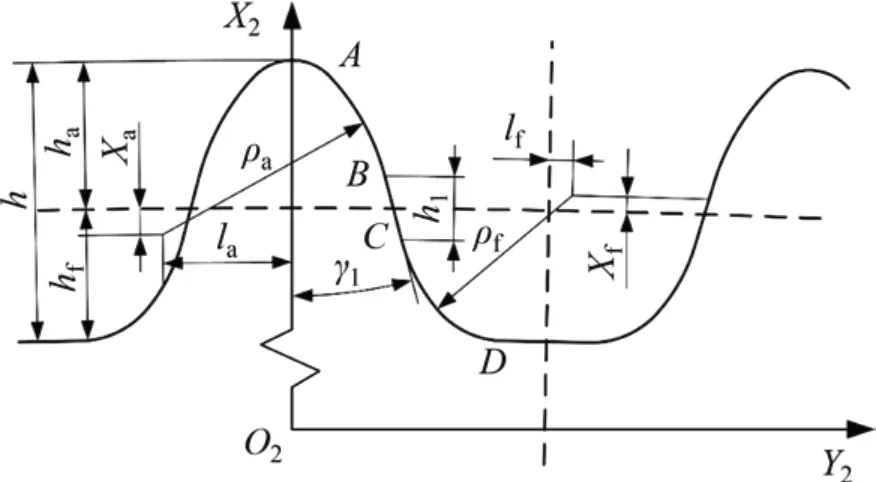
圖3 剛輪雙圓弧齒廓及剛輪坐標系Fig.3 DCTP and coordinate of a circular spline tooth

在剛輪坐標系S2中，柔輪齒圈各截面用不同的Z坐標值zi來表征，根據直母線假設變形后柔輪各截面的徑向變形系數ωi(i=1，2，…，c)可由下式來描述：

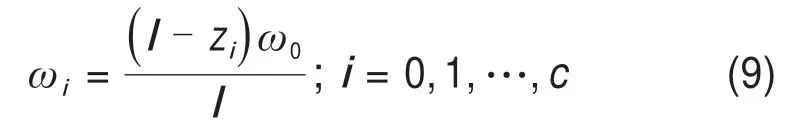
式中：l為設計主截面至杯底距離；zi為剛輪坐標系中各截面坐標值；ω0為波發生器徑向變形系數。

式(9)中c為柔輪齒圈部分所選取的截面的個數，zi∈[2，-10]。將柔輪齒圈部分沿著旋轉軸均分為25個橫截面來表示(c=25)，從第1到第25個橫截面分別對應z=2，1.5，1，…，-10，齒形設計主截面的z=0。

表1 剛輪齒廓參數Table1 Circular spline tooth profile parameters

對于其中的任意一個截面，徑向變形系數ωi可由式(9)求得，空間轉角θ和ξ以及它們對φ1的導數可由式(1)～(4)求得；將以弧長表示的剛輪齒廓上一系列齒廓曲線點所對應的矢徑r2和法向量n2代入式(7)，得出該點發生共軛運動時柔輪輪齒坐標原點的矢徑OO1與波發生器長軸X軸間的夾角φ1，整個剛輪齒面的所有25 個齒廓所求解的φ1構成該齒面的共軛區域，共軛區域由2部分組成分別稱為共軛區域一和共軛區域二，如圖4所示。

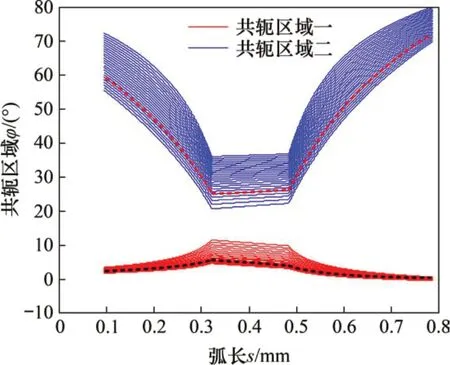
圖4 空間齒廓共軛區域比較Fig.4 Comparison of conjugate existent domain of spatial tooth profiles

圖4中加粗虛線部分表示沒有考慮柔輪空間錐度變形的平面諧波嚙合理論所求解的本例剛輪齒形對應的2個共軛區域，其中黑色虛線表示共軛區域一，紅色虛線表示共軛區域二。由圖4可得平面諧波嚙合理論所求解的共軛區域一角度區間為[-0.461 8°，4.923°]，共軛區域二角度區間為[24.92°，71.66°]；而由本文的算法求得的空間齒廓共軛區域一和二所覆蓋的角度區間為[-0.473 8°，11.44°]和[20.60°，79.94°]。相比平面諧波嚙合理論本文算法共軛區域一的最小角度偏移量和最大角度偏移量分別為0.012°和6.517°，共軛區域二的角度偏移量分別為4.326°和8.287°。用偏移角度和共軛區間大小之比作為共軛區域擴展量的評估參數，則在共軛區域一中最小角度擴展量較小，為0.222 8%，最大角度擴展量為原共軛區間的1.21倍；在共軛區域二中最小角度擴展量為9.255%，最大角度擴展量為17.73%。由于最后計算得到的共軛齒廓受共軛區域一影響較大，以上分析表明本文算法計算所得共軛區域一是平面諧波嚙合理論的2.21 倍，顯著增大了齒形的共軛區域，將使參與共軛嚙合的輪齒數目更多，對提高雙圓弧諧波減速器傳動精度和扭轉剛度、減少輪齒磨損、提高保精度壽命意義重大。

在式(8)中代入由共軛區域求得的坐標變換矩陣M12i，即可得出與剛輪齒廓共軛的柔輪理論齒廓。由于存在2個共軛區域，剛輪每個截面都對應著2個柔輪齒廓。圖5所示為設計截面上與剛輪齒形共軛的柔輪齒廓，2 個齒廓相互分離互不交叉，但它們中只有1個是可行的。圖中黑色柔輪齒廓與平面諧波嚙合理論共軛區域一對應，選擇該齒廓為可行齒廓；紅色齒廓曲線是柔輪齒在遠離凸輪長軸的情況下求解得到的，該齒廓曲線本身存在自相交和折疊，而且在柔輪齒坐標系S1中齒廓x坐標較大，直接作為柔輪齒廓將導致較大的嚙合干涉。

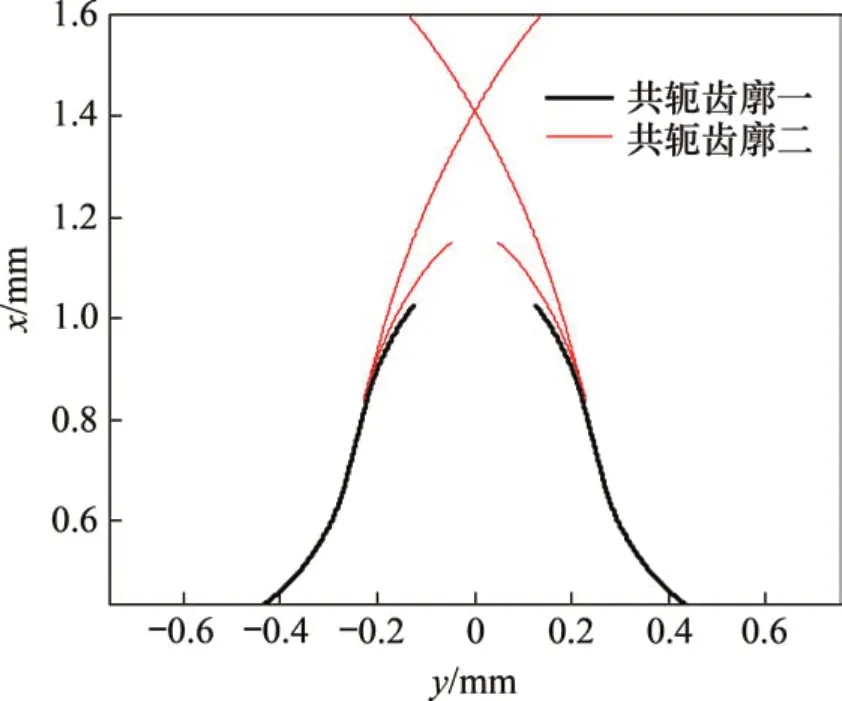
圖5 柔輪平面共軛齒廓Fig.5 Flat flexspline conjugated tooth profiles

因此，對于剛輪齒圈每個截面，都可以采用相同的方法得到與之共軛的柔輪齒廓(如圖6所示)。同樣地，取與共軛區域一相對應的紅色齒廓作為柔輪的空間齒廓，圖7所示為該共軛齒廓的正視圖。由本文模型得到的各截面柔輪空間共軛齒廓不僅考慮了不同截面中面曲線的變化，而且考慮了齒廓曲線所在平面發生的空間轉動。轉動角度由本文的精確空間共軛算法進行計算。

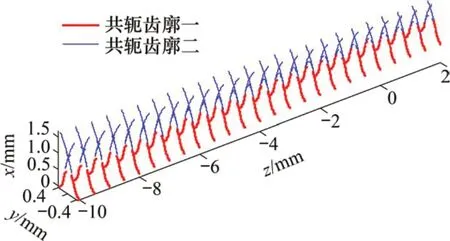
圖6 柔輪空間共軛齒廓Fig.6 Spatial flexspline conjugated tooth profiles

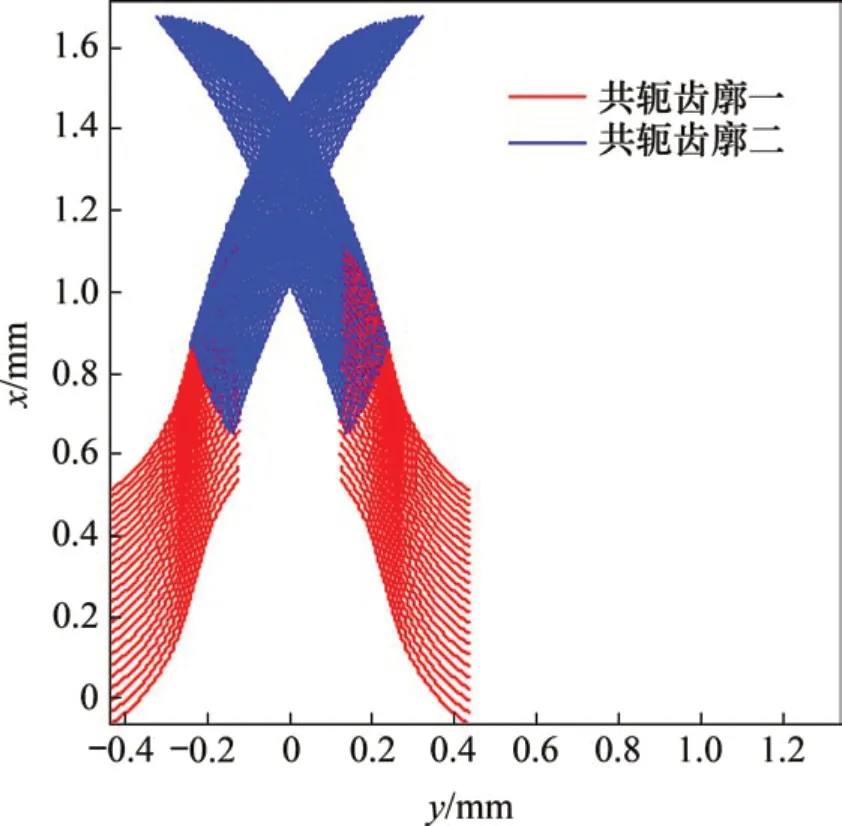
圖7 柔輪空間共軛齒廓Fig.7 Spatial flexspline conjugated tooth profiles

隨著波發生器的轉動，柔輪變形過程中齒圈各截面柔輪齒產生的空間轉角變化曲線分別如圖8和圖9所示，其中，圖8所示為空間轉角θ隨極角φ1的變化規律，圖9所示為空間轉角ξ隨極角φ1的變化規律；θ和ξ兩角度的變化周期為π，用不同的顏色、線形來表示柔輪齒圈沿Z軸各個截面的空間轉角變化規律，每根曲線之間的z坐標之差為2 mm。圖8和圖9中，黑色虛線表示設計截面，綠色虛線表示靠近開口端外側齒圈截面，黑色實線表示靠近輸出端內側截面。從圖8和圖9可見：空間轉角θ波動幅值較大，變化曲線關于180°軸對稱，均值為1.083°，在n·π/2 處出現極值，最大值出現在開口端θmax=1.228°，相比設計截面極值增大了7.16%，相比靠近輸出端內側截面極值增大了8.29%；切向位移v引起的轉角ξ幅值較小，波動曲線關于180°軸反對稱，均值為0°，在(2n+1)·π/4處出現極值，最大值出現在開口端ξmax=0.864 4°，相比設計截面極值增大了1.5倍，相比靠近輸出端內側截面極值增大了1.67倍；柔輪齒圈各截面上2個空間角度均產生了較大的變化，相比空間轉角θ，轉角ξ變化更加劇烈。該曲線變化規律與文獻[20]中徑向位移w、切向位移v的變化規律相吻合。

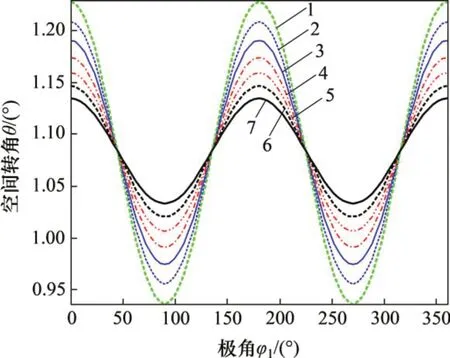
圖8 柔輪齒圈各截面θ角位移曲線Fig.8 Node angular displacement θ on each section of flexspline

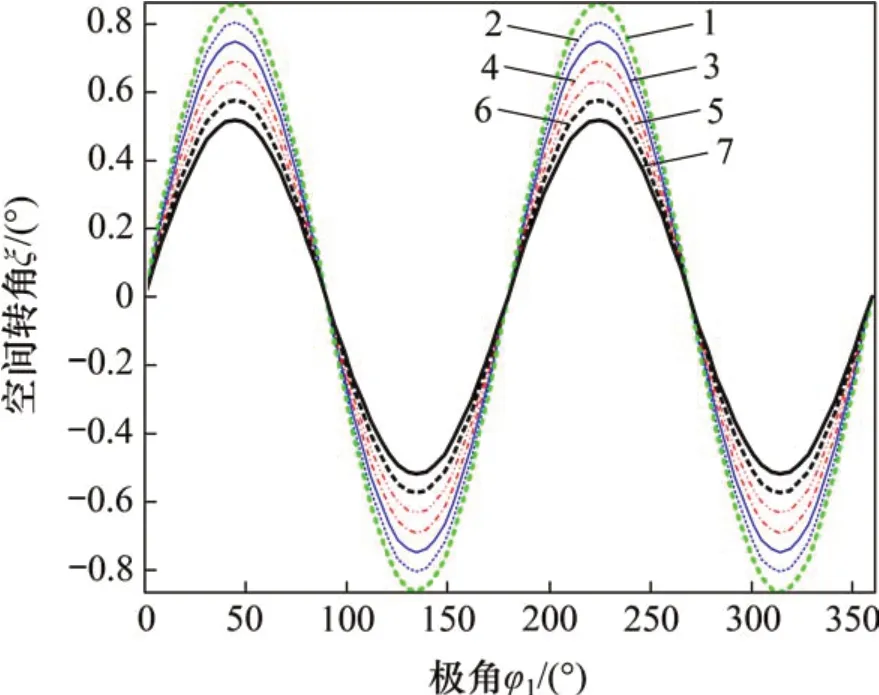
圖9 柔輪齒圈各截面ξ角位移曲線Fig.9 Node angular displacement ξ on each section of flexspline

隨著波發生器的轉動，通過循環增加波發生器的轉角，對各截面柔輪齒廓坐標點進行坐標變換來仿真柔輪齒和剛輪齒的相對運動狀態。在波發生器旋轉0°～360°的過程中，基于本文提出的空間共軛運動學模型的柔輪輪齒相對于剛輪齒槽的運動軌跡如圖10～12 所示。圖10～12 中紅色曲線表示柔輪齒坐標系原點O1的運動軌跡在XY平面的投影，波發生器旋轉1圈，柔輪轉過2個齒。由圖10～12可知：各齒圈截面的剛柔輪嚙合軌跡均未發生干涉，且隨距杯底軸向距離的增大，柔輪齒嚙合運動軌跡的變形量也增大，與實際情況相符。

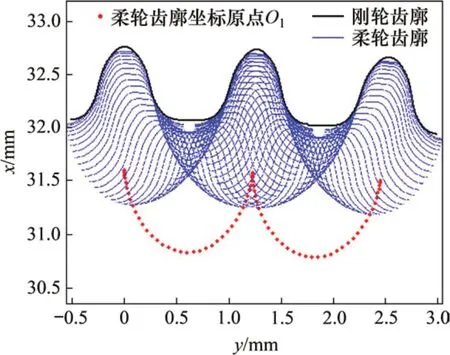
圖10 Z=2截面柔輪齒運動軌跡Fig.10 Relative movement trail of Z=2 section

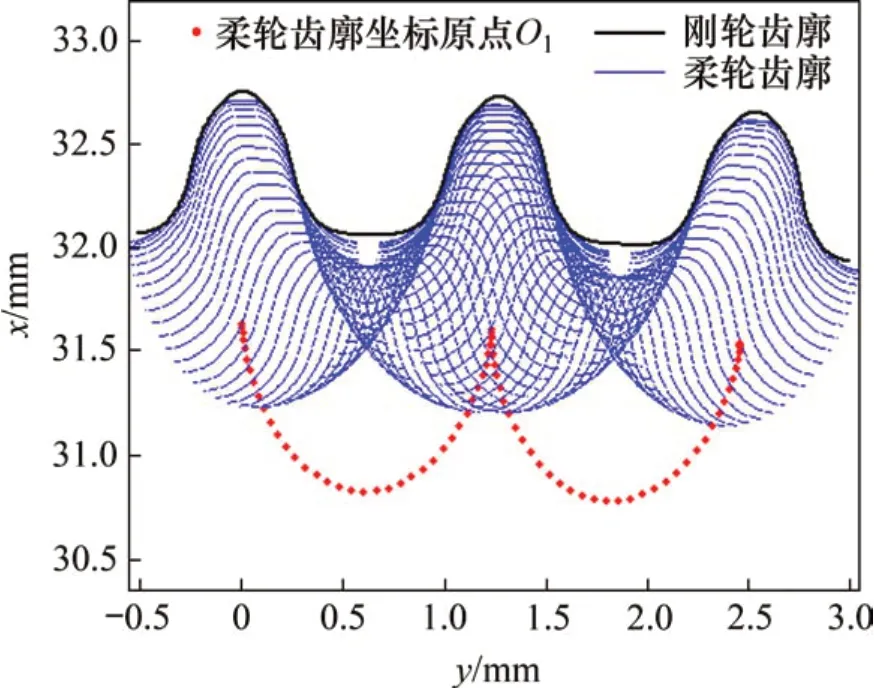
圖11 Z=0截面柔輪齒運動軌跡Fig.11 Relative movement trail of Z=0 section

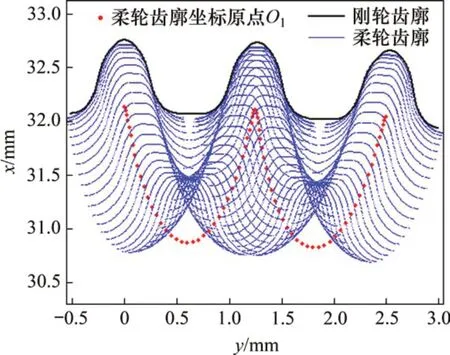
圖12 Z=-10截面柔輪齒運動軌跡Fig.12 Relative movement trail of Z=-10 section

圖13所示為本例柔輪空間齒面上的接觸跡線分布情況，其中，將齒頂部分第1根以及齒根往上第5根標記為綠色，它們是在柔輪輪齒坐標原點矢徑OO1與波發生器長軸X軸間的夾角φ1為2.291 8°時剛、柔輪齒面2 個位置同時發生嚙合接觸形成的，這種現象被稱為兩點接觸現象。從圖13可以看出雙圓弧諧波傳動剛、柔輪齒的嚙合從靠近齒根的位置開始，形成圖13中φ1=0°時的接觸跡線，齒寬方向有超過60%的齒面參與嚙合，此時，波發生器長軸X軸與柔輪輪齒坐標原點矢徑OO1間的夾角為0°；隨著波發生器的轉動，嚙合跡線慢慢從齒根向上擴展，整個齒寬方向全部參與嚙合，直到φ1=2.291 8°時齒頂部也開始出現嚙合接觸，在柔輪齒面出現2根接觸跡線，形成兩點接觸；波發生器繼續轉動時，2根嚙合接觸跡線在齒面中部相遇，最終合成1根，慢慢沿齒寬方向退出嚙合，當φ1=10.886 2°時完全退出嚙合。圖13中嚙合跡線對應的共軛區域為[0°，10.886 2°]，該共軛區域與前面本文算法計算的共軛區域一[-0.473 8°，11.44°]較吻合，與平面諧波嚙合理論相比共軛區域增大。

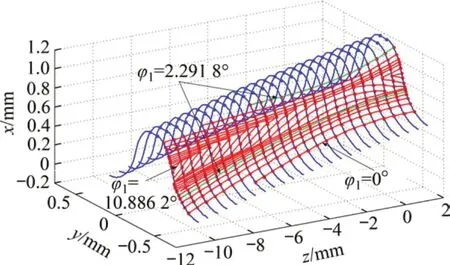
圖13 柔輪齒面嚙合接觸跡線分布Fig.13 Contact path on flexspline tooth surface

4 結論

1)考慮柔輪空間變形帶來的中面曲線變化和柔輪齒空間方位變化等因素，提出一種精確描述剛柔輪之間復雜空間運動關系的運動學模型，能夠便于求解計算空間精確共軛齒廓，所得空間齒廓具有更大的共軛嚙合區域，這對提高諧波減速器承載能力和傳動性能有重要意義。

2)相比平面諧波嚙合理論，本文算法所求解的2個共軛區域均顯著擴大，對共軛齒廓具有顯著影響的共軛區域一擴展了1.21 倍，共軛區域二擴展了17.73%；有更多的齒對參與嚙合，所得柔輪齒面嚙合接觸跡線可精確描述雙圓弧齒形在空間共軛情況下的兩點接觸現象。

3)本文所考慮的柔輪齒圈各截面上由徑向位移和切向位移所引起的2 個空間轉角θ和ξ均發生了較大變化，不可忽視，其中，θmax=1.228°，與設計截面的θmax相比增加8.29%，ξmax=0.864 4°，與設計截面的ξmax相比增幅167%，與由徑向位移w引起的轉角θ相比，切向位移v引起的轉角ξ變化更加劇烈。