有干預措施的 Filippov戒煙模型的全局動力學*
馬慧麗,黃立宏,王佳伏
(長沙理工大學 數學與統計學院 , 湖南 長沙 410114)
1 引 言
吸煙和接觸煙草煙霧是全球公共衛生的一大威脅, 它引發了許多其他疾病并且造成了嚴重的發病率和死亡率, 如癌癥、慢性肺病、心血管疾病和中風等.吸煙行為還具有可傳播性和擴散性, 潛在吸煙者可能通過與吸煙者接觸而吸煙.從某種意義上說吸煙行為與傳染病有類似的傳播機制.因此許多學者運用傳染病傳播原理建立戒煙動力學模型來預防和控制吸煙.如Carlos Castillo-Garsow(1997)等[1]利用傳染病傳播原理建立了一個 SIR 模型來研究戒煙問題, 并分析了所建模型的基本再生數及無煙平衡點和吸煙平衡點的穩定性.李志民等(2019)[2]建立了一類具有非線性發生率的戒煙模型, 并分析了其動力學行為.王霞等(2019)[3]研究了一類帶有非線性接觸率和戒煙不完全成功的戒煙模型, 并研究了該模型平衡點的全局動力學性質.考慮到媒體和政府對吸煙的干預作用, Sharma等(2015)[4]提出了一個非線性數學模型來研究媒體報道對戒煙的影響.Guerrero等(2011)[5]用一個流行病學模型來研究吸煙在西班牙人口(16-65 歲)中的流行演變規律, 發現在 2006 年西班牙無煙立法后在最初幾年的實施中有非常積極的影響.
事實上, 大眾媒體宣傳可促進保護非吸煙者并勸阻人們使用煙草[6].由于眾多經典的微分方程戒煙模型都是右端連續的, 但若考慮到媒體和政府的干預等因素, 建立右端不連續的戒煙模型或能更真實地刻畫人們的吸煙行為.相比于用右端連續微分方程模型描述不連續的干預現象, 右端不連續的Filippov 系統不僅能夠更準確地刻畫這些不連續現象, 而且由于所建 Filippov 模型的不連續性, 使得系統具有更加豐富的動力學行為, 從而揭示出豐富且具有重要生物學意義的新結果.因此將Filippov系統運用到戒煙模型中,運用Filippov定性理論分析模型的動力學行為,從而可以得到政府和媒體干預對戒煙的影響.
2 模型的建立及預備知識
2.1 模型的建立
由于無煙情況是很難實現的,控制吸煙人數在一個合理的范圍更加符合實際.在一些現有工作的基礎上[1-5,7-17], 結合閾值策略, 提出式(1)所示的一個基于干預措施的 Filippov 戒煙模型來研究媒體和政府干預對吸煙傳播的影響.

(1)
其中
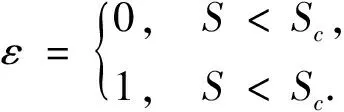
這里所有的參數均為正值.其中P=P(t),S=S(t)分別代表了潛在吸煙者和吸煙者的數量,μ表示潛在吸煙者的出生率,β代表潛在吸煙者與吸煙者的接觸影響率,d1,d2分別代表了潛在吸煙者和吸煙者的死亡率,q表示戒煙率,m表示政府和媒體對吸煙的干預強度.
模型采取如下的閾值策略:
當吸煙者的數量低于臨界水平Sc時, 不采取干預措施, 此時由于基本的健康意識, 一般情況下人們會有戒煙意識和措施, 戒煙率為q;
當吸煙者的數量超過Sc時, 政府和媒體采取干預措施, 減少吸煙人數, 提高戒煙率, 戒煙率為q.
2.2 解的正性和有界性
考慮到系統(1)的現實意義, 這一節討論系統(1)解的正性和有界性.
引理1[10,15]設(P(t),S(t))是系統(1)滿足初值條件P(0)≥0,S(0)≥0且定義在區間[0,T)上的解, 其中T∈(0,+].那么對所有的t∈[0,T),有P(t)≥0,S(t)≥0.
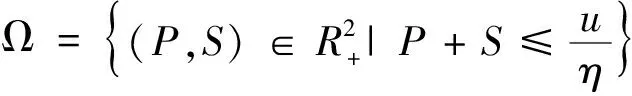
2.3 子系統動力學分析
這個部分主要分析子系統的動力學性質, 在區域G1和G2,系統(1)可以分成子系統(2)和子系統(3).
(2)
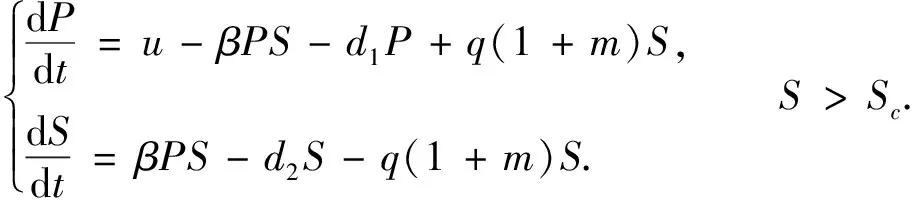
(3)
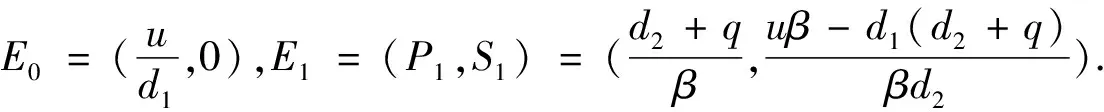
引理3當R1<1 時,E0是子系統(2)的全局漸近穩定的無煙平衡點; 當R1>1時,E1是子系統(2)的全局漸近穩定的吸煙平衡點.
證明系統(2)的 Jacobian 矩陣為

由特征方程|J(E1)-λI|=0知, 特征根為
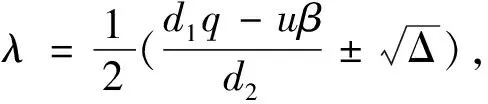
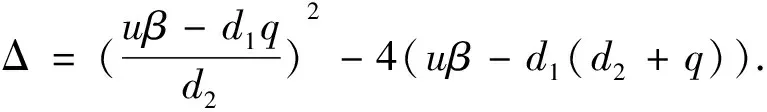

類似地, 采用引理3的證明方法可以得到下面的結論.
引理4當R2<1時,E0是子系統(3)的全局漸近穩定的無煙平衡點; 當R2>1時,E2是子系統(3)的全局漸近穩定的吸煙平衡點.
2.4 滑模域和滑模方程
本節討論系統(1)的滑模動力學.
首先來討論滑模區域的存在性.取法向量為n=(0,1), 由 〈n,F1(P,Sc)〉〈n,F2(P,Sc)〉<0可知滑模區域存在且為
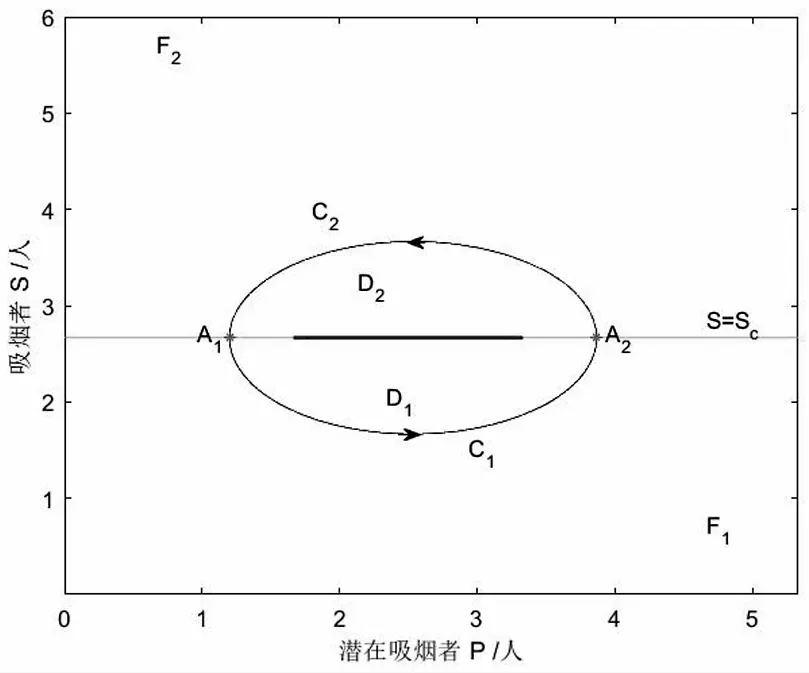
Σs={(P,S)|P1 其中P1和P2分別為切點T1和T2的橫坐標.根據 Filippov 凸方法[18]可知系統(1)在Σs上的滑模方程為 (4) 本節討論系統(1)的全局漸近穩定性, 首先來排除系統(1)的閉軌. 圖1 可能存在圍繞的閉軌示意圖 (5) 在區域D1內運用格林公式, 可以得到 因為A2>A1, 那么 圖2 當E1為實,E2為虛時, 可能存在包含部分的閉軌示意圖 引理7[18]如果系統(1)的正半軌T+是有界的, 那么它的極限集Ω(T)要么包含一個平衡點, 要么包含一個閉軌. 定理1當R1<1時, 系統(1)的無煙平衡點E0是全局漸近穩定的. 證明由于R2 f(P1)=-d1P1+u-d2Sc=d2(S1-Sc)<0,f(P2)=d2(S2-Sc)<0. 即f(P)<0當P∈(P1,P2), 這說明此時偽平衡點不存在.此外分別由引理1和引理2可知,系統(1)的解是有界的, 并且無任何形式的閉軌.那么根據引理7, 此時唯一的實平衡點E0是系統(1)的ω極限集, 即當R1<1時,無煙平衡點E0是全局漸近穩定的, 如圖3所示. 其中參數取值為:u=3,d1=0.2,d2=0.6,β=0.02,q=0.1,m=4,Sc=7. 當R1>1時, 由于P1 定理 2 當R1>1時, 下面結論成立: (i)當0 (ii)當S1>Sc,S2>Sc時, 實平衡點E2是全局漸近穩定的; (iii)當S2 證明 首先來證明結論(i).當0 f(P1)=d2(S1-Sc)<0,f(P2)=d2(S2-Sc)<0. 即在區間(P1,P2)上f(P)<0, 這說明此時偽平衡點不存在.在系統(1)解有界并且無閉軌的情況下, 由引理7 可得出唯一的實平衡點E1是全局漸近穩定的, 如圖 4 所示.類似地, 也可以得出結論(ii): 當S1>Sc,S2>Sc時, 實平衡點E2是全局漸近穩定的, 如圖5所示. 圖4 吸煙平衡點E1的全局漸近穩定的平面相圖 圖5 吸煙平衡點E2的全局漸近穩定的平面相圖 接下來證明結論(iii).當S2 f(P1)=d2(S1-Sc)>0,f(P2)=d2(S2-Sc)<0. 此時函數f(P)在區間(P1,P2)上有唯一的一個零點P*,這說明滑模上有一個偽平衡點E*=(P*,Sc).由于在區間(P1,P*)上f(P)>0, 在區間(P*,P2)上f(P)<0, 那么偽平衡點E*在滑模上是穩定的.在系統(1)的解有界并且無閉軌的情況下, 可得出: 當S2 圖6 偽平衡點E*的全局漸近穩定的平面相圖 其中參數取值為:u=10,d1=0.2,d2=0.6,β=0.1,q=0.1,m=4,Sc=20. 其中參數取值為:u=10,d1=0.2,d2=0.6,β=0.1,q=0.1,m=4,Sc=8. 其中參數取值為:u=10,d1=0.2,d2=0.6,β=0.1,q=0.1,m=8,Sc=13. 提出了一類 Filippov 戒煙模型來研究媒體和政府干預對戒煙的影響.分析了模型的全局動力學性質,得到了各類平衡點的全局漸近穩定的動力學性質.當R1<1時, 平衡點E0是全局漸近穩定的,表明吸煙人數將隨著時間推進而趨于0.當R1>1時, 干預強度m與S2成反比, 即當干預強度m越大,S2越小.當S2
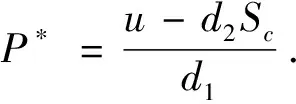
2.5 閉軌的排除


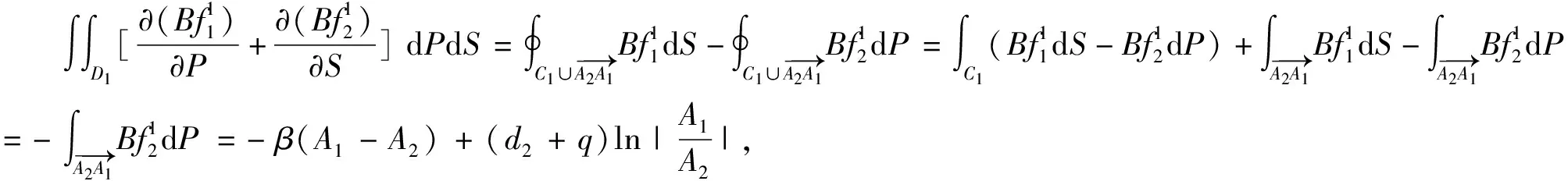
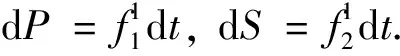
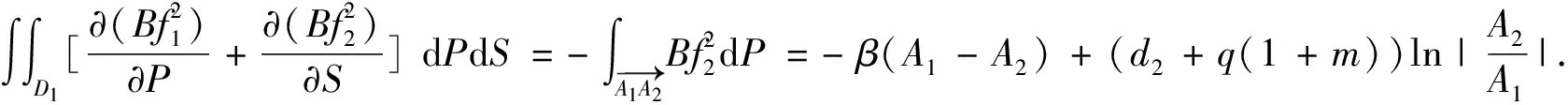
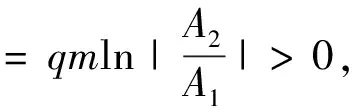


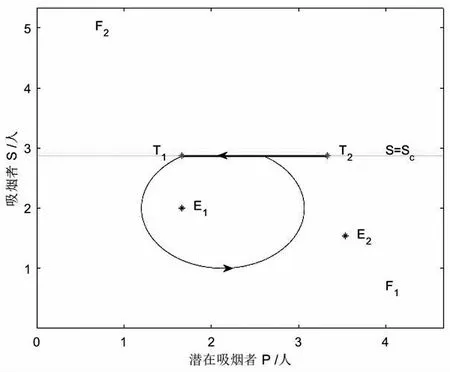
3 全局動力學分析

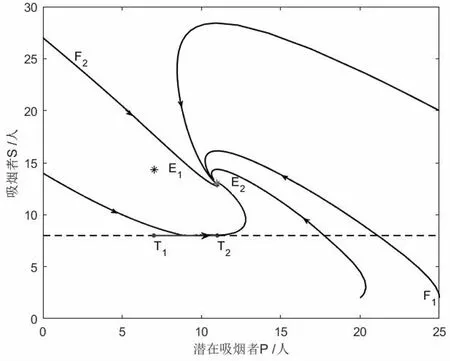
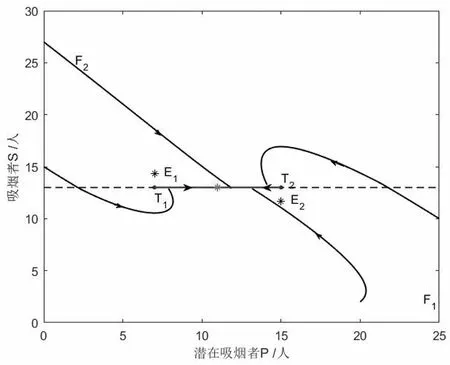
4 結 論

