用換元法解含有雙未知角的三角函數求值問題

山東省淄博市淄博中學 王強珠 趙圣濤

換元法是高中數學重要的解題方法之一，通過換元法，可以把復雜問題簡單化，進而達到求解的目的。三角函數中的求值問題是高考常見題型之一，在求解該類問題時，常規思路是尋找已知角與待求角之間的聯系，通過角之間的轉化實現問題的解決，但在教學過程中，筆者發現學生在尋找角與角之間的關系時常存在困難，特別是數學思維力較弱的學生尤為明顯。基于此，筆者在教學中探索出了用換元法解決該類問題的策略，該方法具有思維量小、思路簡單清晰的特點，現將方法介紹如下。

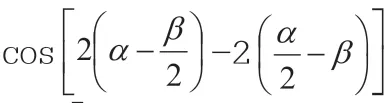
點評：上述例題中，我們利用換元法，借助方程組，把已知角α、β 用角x，y 表示出來，再代入所求的cos（α+β）中，將問題轉化為關于角x，y 的三角函數求值問題，從而實現問題的解決。

通過上述兩個實例我們發現，通過換元代入后，能直接發現條件中的已知角和所求角之間的關系，解決了教學中學生正面解決時無法發現角的關系的問題。