基于納什討價還價下的利率互換收益分配
林昊琦

摘要:利率互換的收益是指兩個借款人通過合作發揮各自比較優勢而獲得的合作收益,利率互換的收益分配可以歸屬為二人合作博弈問題。我們通過構建博弈樹,建立“納什討價還價解”模型并對模型進行適用性分析及解法分析,得出結論為:雙方平分互換收益。
關鍵詞:利率互換 收益分配 合作博弈 博弈樹 納什討價還價解
一、引言
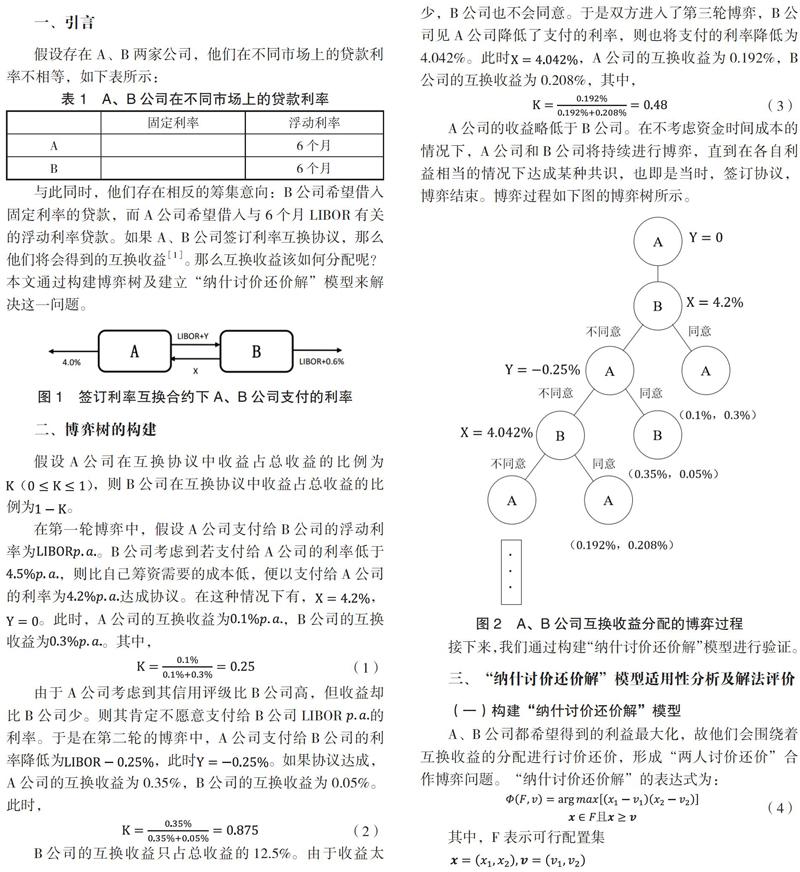
假設存在A、B兩家公司,他們在不同市場上的貸款利率不相等,如下表所示:
與此同時,他們存在相反的籌集意向:B公司希望借入固定利率的貸款,而A公司希望借入與6個月LIBOR有關的浮動利率貸款。如果A、B公司簽訂利率互換協議,那么他們將會得到的互換收益[1]。那么互換收益該如何分配呢?本文通過構建博弈樹及建立“納什討價還價解”模型來解決這一問題。
二、博弈樹的構建
假設A公司在互換協議中收益占總收益的比例為,則B公司在互換協議中收益占總收益的比例為。
由于A公司考慮到其信用評級比B公司高,但收益卻比B公司少。則其肯定不愿意支付給B公司LIBOR的利率。于是在第二輪的博弈中,A公司支付給B公司的利率降低為,此時。如果協議達成,A公司的互換收益為0.35%,B公司的互換收益為0.05%。此時,
B公司的互換收益只占總收益的12.5%。由于收益太少,B公司也不會同意。于是雙方進入了第三輪博弈,B公司見A公司降低了支付的利率,則也將支付的利率降低為4.042%。此時,A公司的互換收益為0.192%,B公司的互換收益為0.208%,其中,
A公司的收益略低于B公司。在不考慮資金時間成本的情況下,A公司和B公司將持續進行博弈,直到在各自利益相當的情況下達成某種共識,也即是當時,簽訂協議,博弈結束。博弈過程如下圖的博弈樹所示。
接下來,我們通過構建“納什討價還價解”模型進行驗證。
三、“納什討價還價解”模型適用性分析及解法評價
(一)構建“納什討價還價解”模型
A、B公司都希望得到的利益最大化,故他們會圍繞著互換收益的分配進行討價還價,形成“兩人討價還價”合作博弈問題。“納什討價還價解”的表達式為:
(二)“納什討價還價解”模型適用性分析
此博弈屬于合作博弈。如果合作博弈的可行配置集不滿足“凸集”、“非空且有界”的條件,則合作博弈模型失去了計算的意義。下面我們進行證明:
(三)“納什討價還價解”模型解法分析
我們由“納什討價還價解”的表達式及限制條件解得。我們認為其滿足以下五個公理的即為公平的解[2]。下面我們進行驗證:
由此可見,為公平的解。
四、結論
綜合研究說明,只要兩家公司在兩個利率市場的利率差不相等,且存在相反的籌資意向時,互換收益就會存在,利率互換交易必會進行[1]。在簽訂協議的過程中,雙方將會圍繞互換利率分配的問題進行討價還價。根據博弈樹及“納什討價還價解”模型,我們得出最終敲定的結果為:雙方平分收益。文中的研究思路以及模型不僅僅適用于利率互換收益的分配,還可推廣到貨幣互換收益的分配等兩人合作博弈的討價還價這一類問題。
參考文獻:
[1][加]約翰·赫爾.期權與期貨市場基本原理(原書第7版)[M].北京:機械工業出版社,2013:114-122.
[2]荀旸. 基于合作博弈的企業薪酬分配模型研究[D].哈爾濱理工大學,2017.
作者單位:華南師范大學

