淺海聲速剖面結(jié)構(gòu)變化對(duì)聲吶作用距離的影響

趙建昕，過(guò)武宏

（海軍潛艇學(xué)院，山東 青島 266199）

聲吶作用距離是水聲環(huán)境應(yīng)用中的重要指標(biāo)，對(duì)它的預(yù)報(bào)不僅依賴(lài)于聲傳播模型，而且還決定于海洋環(huán)境參數(shù)和目標(biāo)特性。聲傳播速度是海洋環(huán)境參數(shù)溫度、鹽度和靜壓力的函數(shù)，是影響聲傳播最基本的物理參數(shù)，它的不確定性將影響聲吶作用距離[1]。

笪良龍[1]以某個(gè)聲速剖面為基準(zhǔn)，利用蒙特卡洛方法獲取聲速剖面的不確定性，進(jìn)而研究了聲吶作用距離的隨機(jī)分布，得到了聲速的隨機(jī)不確定性到聲吶作用距離不確定性的傳遞規(guī)律。聲速剖面結(jié)構(gòu)變化也是一種聲速不確定性的表現(xiàn)，它對(duì)聲傳播的影響巨大。這方面現(xiàn)有研究成果主要包括：張旭等[2]研究了聲躍層結(jié)構(gòu)變化對(duì)深海匯聚區(qū)聲傳播的影響；潘長(zhǎng)明等[3]研究了淺海溫躍層對(duì)水聲傳播損失場(chǎng)的影響；莊益夫等[4]研究了深海聲速剖面結(jié)構(gòu)變化對(duì)會(huì)聚區(qū)偏移特性的影響分析。李佳等[5]研究了印度洋中北部聲速剖面結(jié)構(gòu)的時(shí)空變化及其形成機(jī)理。謝亮等[6]討論了海洋混合層聲速剖面的結(jié)構(gòu)對(duì)聲傳播的影響。馬志康等[7]研究了臺(tái)風(fēng)對(duì)混合層聲速剖面的擾動(dòng)帶來(lái)的聲傳播的影響。本文將重點(diǎn)研究淺海環(huán)境中均勻?qū)印⒇?fù)梯度、正梯度和負(fù)躍層4 種聲速剖面不同結(jié)構(gòu)變化對(duì)聲吶作用距離的影響。

1 聲速剖面模型

聲速剖面反映了一定范圍海區(qū)的聲速垂直結(jié)構(gòu)，對(duì)水聲傳播影響巨大。針對(duì)淺海環(huán)境的特點(diǎn)，本文主要研究4 類(lèi)聲速剖面：均勻?qū)勇曀倨拭妗⒇?fù)梯度聲速剖面、正梯度聲速剖面和負(fù)躍層聲速剖面，并利用解析函數(shù)模型來(lái)模擬聲速剖面，通過(guò)調(diào)整模型中的參數(shù)得到聲速剖面的結(jié)構(gòu)變化。

負(fù)梯度和正梯度聲速剖面利用布列霍夫斯基[8]給出的聲速剖面解析公式：

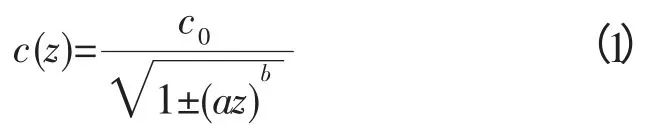
式中：a 為尺度參數(shù)；b 為形狀參數(shù)，不同取值可以得到不同的凹凸曲線(xiàn)。

負(fù)躍層聲速剖面，首先利用GDEM（Generalized Digital Environmental Model）模型[9-10]的冪函數(shù)形式描述海洋溫躍層結(jié)構(gòu)，具體為[9]：

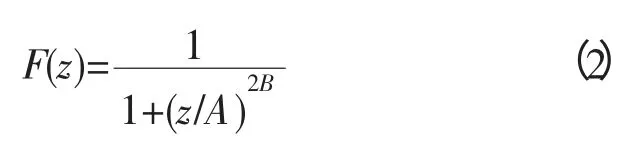
式中：z 表示水深；A 表示躍層的平均深度；B 表示躍層中溫度梯度的變化率。再次利用式（3）的線(xiàn)性映射得到具有式（2）結(jié)構(gòu)的隨深度變化的溫度函數(shù)：

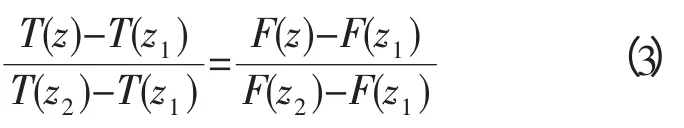
式中：T(z)表示溫度；z1，z2為躍層頂部和躍層底部的位置，于是淺海溫躍層的結(jié)構(gòu)為：

進(jìn)一步，結(jié)合Wilson 公式[8]

2 數(shù)值仿真

采用Kraken 模型來(lái)計(jì)算聲場(chǎng)，主要參數(shù)見(jiàn)表1，水深80 m，頻率100 Hz，優(yōu)質(zhì)因子選擇了75 dB 和80dB 兩種，用來(lái)比較不同的優(yōu)質(zhì)因子在計(jì)算聲吶作用距離時(shí)，對(duì)于聲吶作用距離不確定性的影響。對(duì)于均勻?qū)印⒇?fù)梯度和正梯度聲速剖面，聲源深度選擇7 m，接收深度選擇15 m。對(duì)于負(fù)躍層聲速剖面，聲源深度和接收深度分別選擇7 m 和15 m，7 m 和40 m，15 m 和 7 m，40 m 和 7 m 這 4 種情形，旨在研究聲源和接收器在躍層上、下時(shí)，對(duì)于聲吶作用距離不確定性的影響。在以下的分析中，首先根據(jù)表1 中的聲速剖面模型建立一個(gè)參考剖面，通過(guò)改變模型參數(shù)控制剖面的結(jié)構(gòu)變化，進(jìn)而討論這些變化對(duì)聲吶作用距離產(chǎn)生的影響。

聲吶作用距離是利用非相干方法得到的聲場(chǎng)傳播損失和優(yōu)質(zhì)因子相等計(jì)算得到。

表1 Kraken 聲傳播模型的主要參數(shù)

2.1 均勻?qū)勇曀倨拭?/h3>

選擇聲速為 1 510～1 528 m/s，間隔為 2 m/s 的均勻?qū)勇曀倨拭妫?jiàn)圖1 的左側(cè)子圖，右側(cè)子圖給出了不同的聲速剖面，優(yōu)質(zhì)因子為75 dB 時(shí)，對(duì)應(yīng)的聲吶作用距離，距離的變化范圍是[8 650， 10 650]m，最大誤差達(dá)到2 000 m，最大誤差與聲吶作用距離的最小值比為23%，可見(jiàn)均勻?qū)勇曀倨拭娴恼`差對(duì)聲吶作用距離有影響。2 m/s 的誤差帶來(lái)的聲吶作用距離的估計(jì)誤差相差200 m 以上，當(dāng)優(yōu)質(zhì)因子選擇80 dB時(shí)，距離的變化范圍是[27 300， 33 550]m，最大誤差達(dá)到6 250 m，最大誤差與聲吶作用距離的最小值比為23%，2 m/s 的誤差帶來(lái)的聲吶作用距離的估計(jì)誤差相差650 m 以上。可見(jiàn)隨著優(yōu)質(zhì)因子的增加，雖然聲吶作用距離大了，但是估計(jì)的最大誤差在增加，原因就是聲吶作用距離的估計(jì)方法，非相干方法得到的聲場(chǎng)的傳播損失曲線(xiàn)，如圖2 所示，隨著水平距離的增加，曲線(xiàn)的梯度絕對(duì)值趨小，帶來(lái)的影響是，當(dāng)聲速剖面有誤差代入時(shí)，同樣的優(yōu)質(zhì)因子的聲吶作用距離估計(jì)變化大，導(dǎo)致了上述結(jié)果。

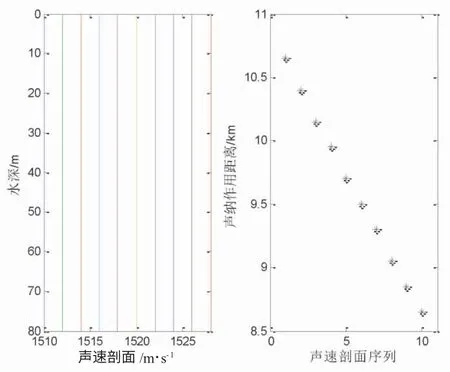
圖1 均勻?qū)勇曀倨拭婕捌渎晠茸饔镁嚯x

2.2 負(fù)梯度聲速剖面

負(fù)梯度聲速剖面由式（1）獲得，其中參數(shù)b 是形狀參數(shù)，可用來(lái)刻化曲線(xiàn)的凹凸性的，選擇了b=0.5，1.2 分別表示曲線(xiàn)上凸和下凸，不同的a 值的選擇見(jiàn)表2，表示聲速剖面在海面的聲速變化大，還是海底聲速變化大，見(jiàn)圖3～圖6 的左側(cè)子圖，表達(dá)了凹凸性確定情形下，不同的聲速剖面，由此構(gòu)成了4類(lèi)不同的負(fù)梯度聲速剖面。

圖2 均勻?qū)勇晥?chǎng)傳播損失

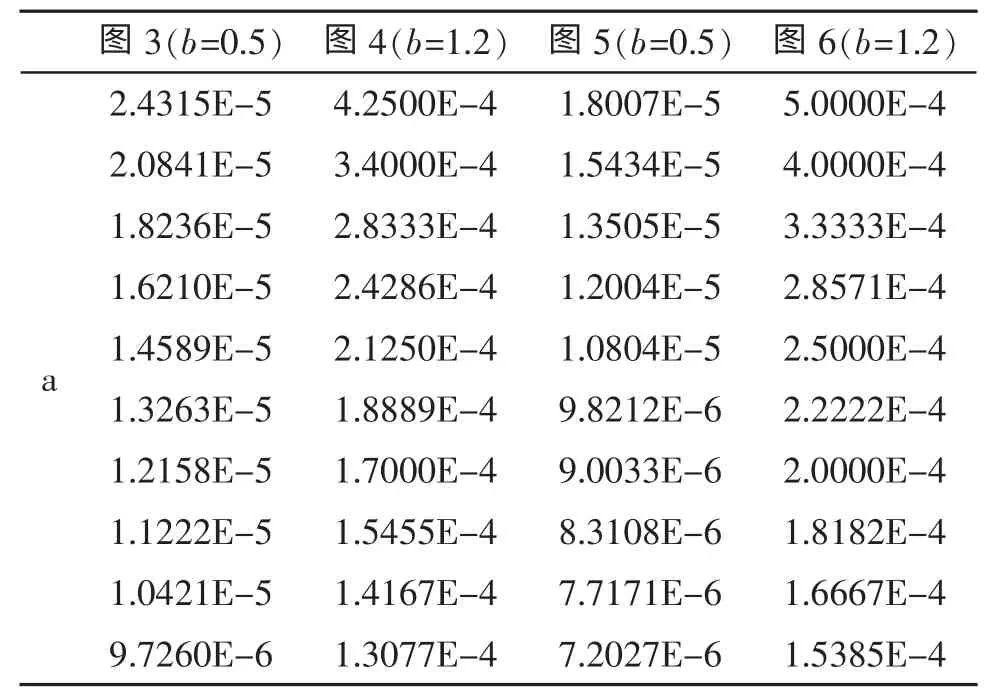
表2 負(fù)梯度聲速剖面模型的主要參數(shù)

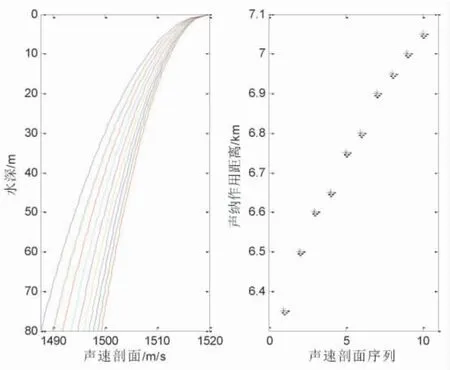
圖3 上凸1 型負(fù)梯度聲速剖面及聲吶作用距離

圖4 上凸2 型負(fù)梯度聲速剖面及聲吶作用距離

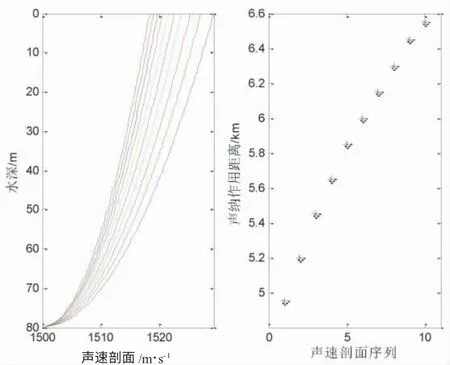
圖5 下凸1 型負(fù)梯度聲速剖面及聲吶作用距離

圖6 下凸2 型負(fù)梯度聲速剖面及聲吶作用距離

圖3～圖6 給出聲源深度7 m，接收深度15 m，優(yōu)質(zhì)因子為75 dB 的仿真結(jié)果。各圖的左側(cè)子圖是聲速剖面圖，右側(cè)子圖是不同聲速剖面的聲吶作用距離，表3 列出了4 種情形下的聲吶作用距離。表3 可見(jiàn)，聲吶作用距離范圍分別是[6 350，7 050]m，[6 250，8 850]m，[4 950，6 550]m 和 [5 450，7 050]m。圖3 和圖5 對(duì)應(yīng)的海底和海面的聲速誤差是一樣的，對(duì)應(yīng)的最大誤差分別為700 m 和1 600 m，最大誤差與聲吶作用距離的最小值比分別是11%和32%，由此得到海面聲速誤差對(duì)聲吶作用距離的影響更大。圖4 和圖6 對(duì)應(yīng)的海面和海底的聲速誤差是一樣的，對(duì)應(yīng)的最大誤差分別是2 600 m 和1 600 m，最大誤差與聲吶作用距離的最小值比分別是42%和29%，由此得到海面聲速誤差對(duì)聲吶作用距離的影響更大。由表3 計(jì)算結(jié)果看，負(fù)梯度的聲速剖面結(jié)構(gòu)誤差對(duì)于聲吶作用距離影響大，最小的占比誤差為11%，最大的占比誤差高達(dá)42%。海底和海面同樣的聲速誤差，海面的聲速誤差相比于海底聲速的誤差對(duì)于聲吶作用距離影響更大。表2 和表3 實(shí)質(zhì)上建立了給定參數(shù)b 取值，不同參數(shù)a 取值下，聲吶作用距離的定量變化規(guī)律。此外，當(dāng)優(yōu)質(zhì)因子增大時(shí)，聲吶作用距離的最大誤差有加大的趨勢(shì)，與2.1 中結(jié)果類(lèi)似。

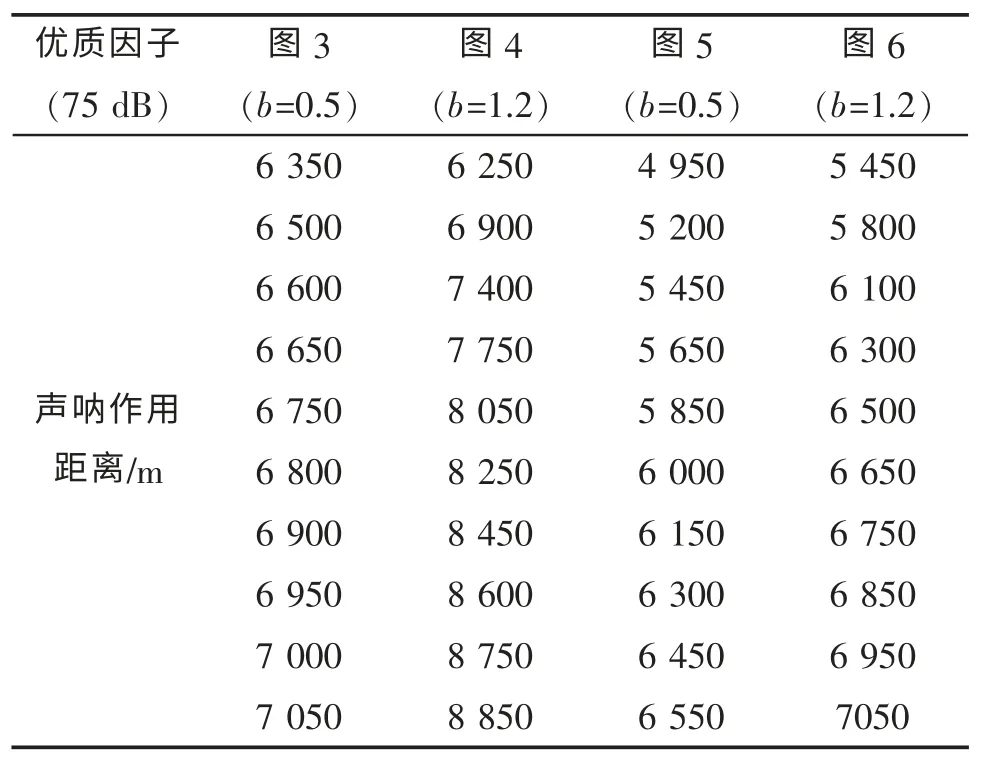
表3 負(fù)梯度聲速剖面下聲吶作用距離（聲源深度7 m，接收深度15 m）

2.3 正梯度聲速剖面

正梯度聲速剖面由式（1）獲得，同2.2，參數(shù)b是刻化曲線(xiàn)的凹凸性的，選擇了b=0.4，0.5，1.2 分別表示曲線(xiàn)上凸和下凸，不同的a 值的選擇見(jiàn)表4，表示了聲速剖面是海面聲速變化大，還是海底聲速變化大，由此構(gòu)成了4 類(lèi)不同的正梯度聲速剖面。

圖7～圖10 給出了聲源深度7 m，接收深度15 m，優(yōu)質(zhì)因子為75 dB 的仿真結(jié)果，表5 列出了4 種情形下的聲吶作用距離。由表5 可見(jiàn)，聲吶的作用距離范圍分別是 [20 000，27 550]m，[11 200，19 950]m，[22 500，35 300]m 和[13 150，195 00]m。圖 7 和圖 9 對(duì)應(yīng)的海底和海面的聲速誤差是基本一樣的，對(duì)應(yīng)的最大誤差分別是7 550 m 和12 800 m，最大誤差與聲吶作用距離的最小值比分別是38%和57%，由此得到海面聲速誤差對(duì)聲吶作用距離的影響更大。圖8，圖10 對(duì)應(yīng)的海面和海底的聲速誤差是一樣的，對(duì)應(yīng)的最大誤差分別是8 750 m 和6 350 m，最大誤差與聲吶作用距離的最小值比分別是78%和48%，由此得到海面聲速誤差對(duì)聲吶作用距離的影響更大。由表5 中的計(jì)算結(jié)果看，正梯度的聲速剖面結(jié)構(gòu)誤差對(duì)于聲吶作用距離影響大，最小的占比誤差為38%，最大的占比誤差高達(dá)78%。海底和海面同樣的聲速誤差，海面的聲速誤差相比于海底聲速的誤差對(duì)于聲吶作用距離影響更大。表2 和表3 實(shí)質(zhì)上建立了給定參數(shù)b 取值，不同參數(shù)a 取值下，聲吶作用距離的變化規(guī)律。表4 和表5 實(shí)質(zhì)上建立了給定參數(shù)b 取值，不同參數(shù)a 取值下，聲吶作用距離的變化規(guī)律。當(dāng)優(yōu)質(zhì)因子增大時(shí)，聲吶作用距離的最大誤差有加大的趨勢(shì)，與2.1 中結(jié)果類(lèi)似。

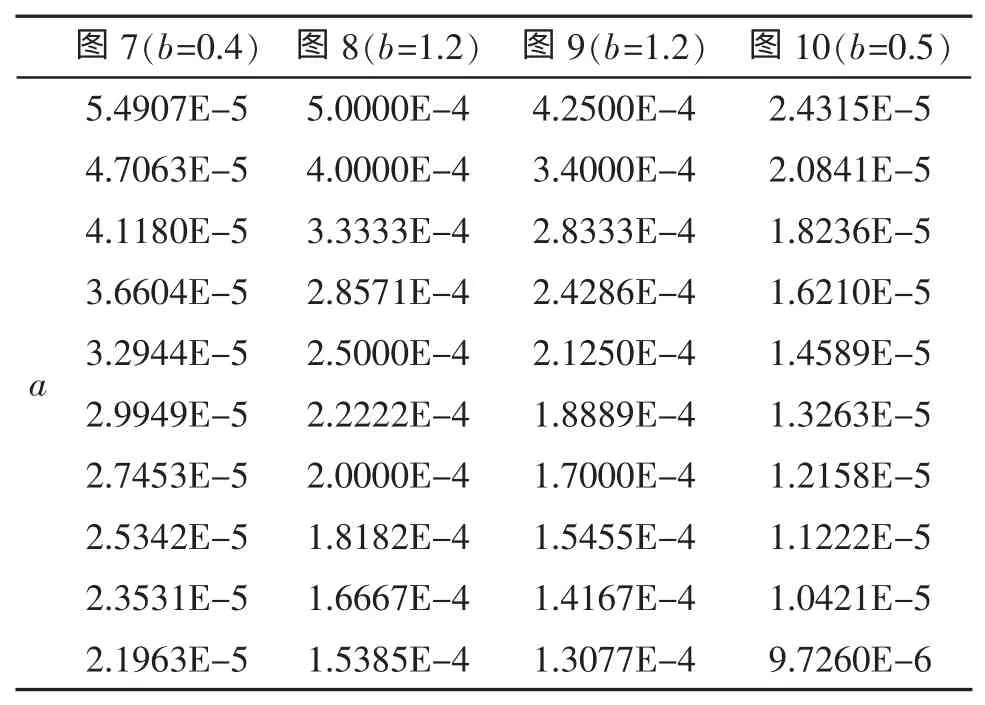
表4 正梯度聲速剖面模型的主要參數(shù)

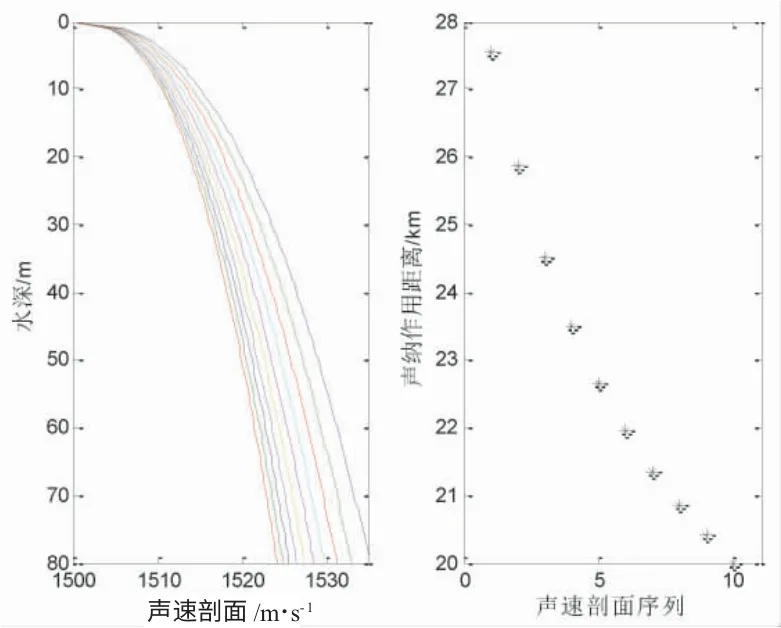
圖7 上凸1 型正梯度聲速剖面及聲吶作用距離

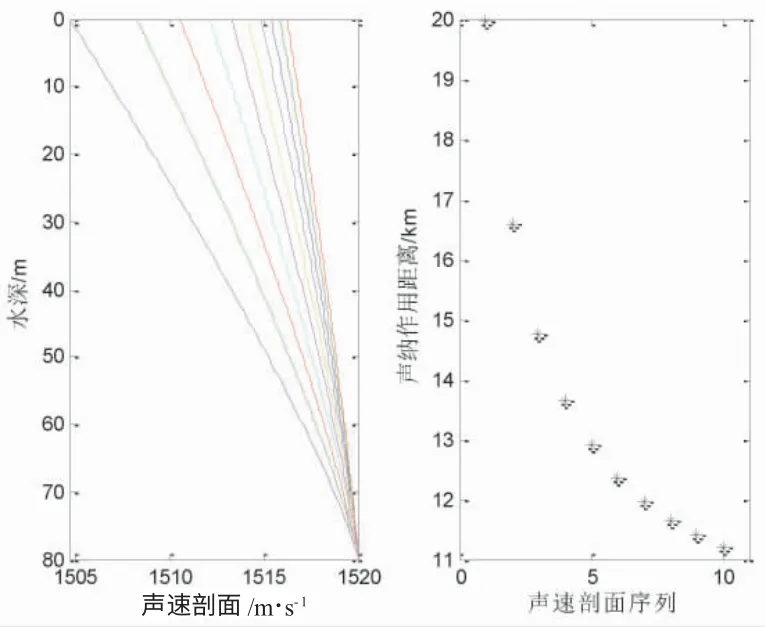
圖8 上凸2 型正梯度聲速剖面及聲吶作用距離

圖9 下凸1 型正梯度聲速剖面及聲吶作用距離

圖10 下凸2 型正梯度聲速剖面及聲吶作用距離

表5 正梯度聲速剖面下聲吶作用距離（聲源深度7 m，接收深度15 m）

2.4 負(fù)躍層聲速梯度

負(fù)躍層聲速剖面由式（4）和Wilson 公式計(jì)算得到，其中參數(shù)A 表示躍層的平均深度；B 表示躍層中溫度梯度的變化率。考慮了固定躍層深度，A=20的兩類(lèi)負(fù)躍層聲速剖面，一是變溫度梯度變化率B見(jiàn)表6 的第2 列和第3 列，分別對(duì)應(yīng)不同的接收深度15 m 和40 m；二是溫度梯度變化率B=2，選擇不同的海表溫度，即躍層以上的均勻?qū)勇曀偈亲兓模?jiàn)表6 的最后兩列，對(duì)應(yīng)著不同的聲源深度15 m和40 m。

圖11～圖14 給出了優(yōu)質(zhì)因子為75 dB 的仿真結(jié)果，表7 列出了4 種情形下的聲吶作用距離。由表7 可見(jiàn)，聲吶作用距離范圍分別是[3100，3550]m，[2800，3250]m，[3700，4600]m 和[2750，3750]m。圖 11和圖12 是負(fù)躍層厚度20 m，不同的接收器深度，聲吶作用距離隨著溫度梯度變化率的變化情況，結(jié)果顯示溫度梯度變化率對(duì)聲吶作用距離有影響。圖11和圖12 顯示同樣的聲源深度下，接收器在躍層以上或以下，聲吶作用距離的最大誤差均是450 m，最大誤差與聲吶作用距離的最小值比分別是15%和16%。圖13 和圖14 是負(fù)躍層厚度20 m， 溫度梯度變化率均為2，不同的聲源深度，聲吶作用距離隨著躍層以上均勻?qū)勇曀俚淖兓闆r，結(jié)果顯示，均勻?qū)勇曀俚淖兓瘜?duì)聲吶作用距離有影響，而不同的聲源深度，分別選擇15 m 和40 m，聲吶作用距離最大誤差分別是900 m 和1 000 m，最大誤差相對(duì)于聲吶作用距離的最小值分別是24%和36%，相比于接收器的誤差占比，聲源深度的影響更大。表6 和表7本質(zhì)上建立了溫度梯度變化率、均勻?qū)勇曀倥c聲吶作用距離的定量關(guān)系。

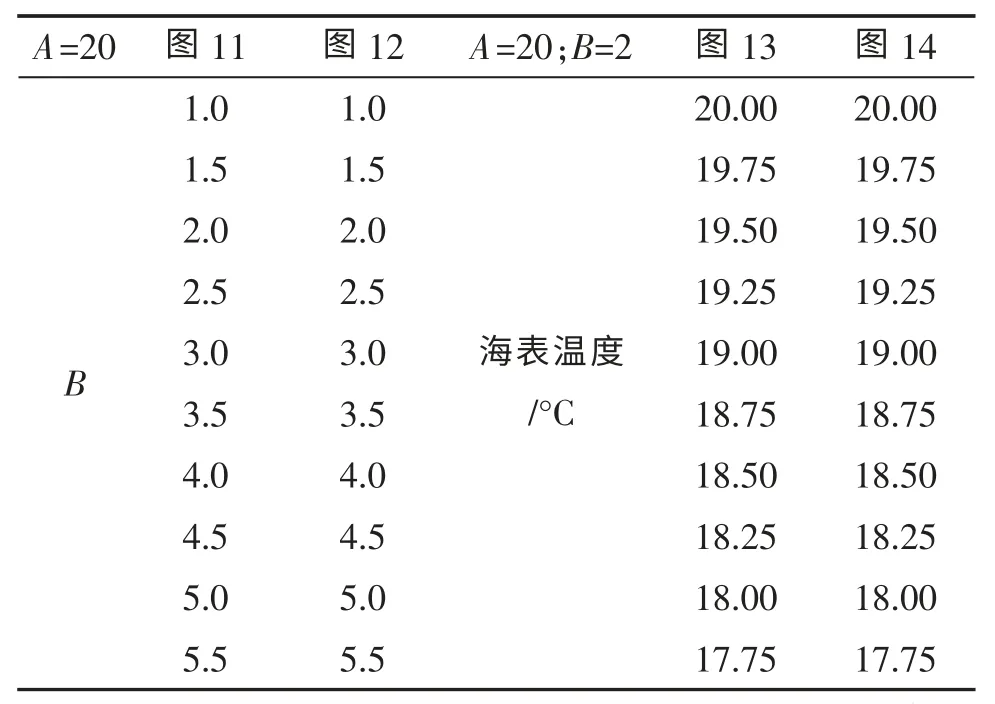
表6 負(fù)躍層聲速剖面模型的主要參數(shù)

圖11 變溫度梯度變化率的聲速剖面及聲吶作用距離（接收深度15 m）

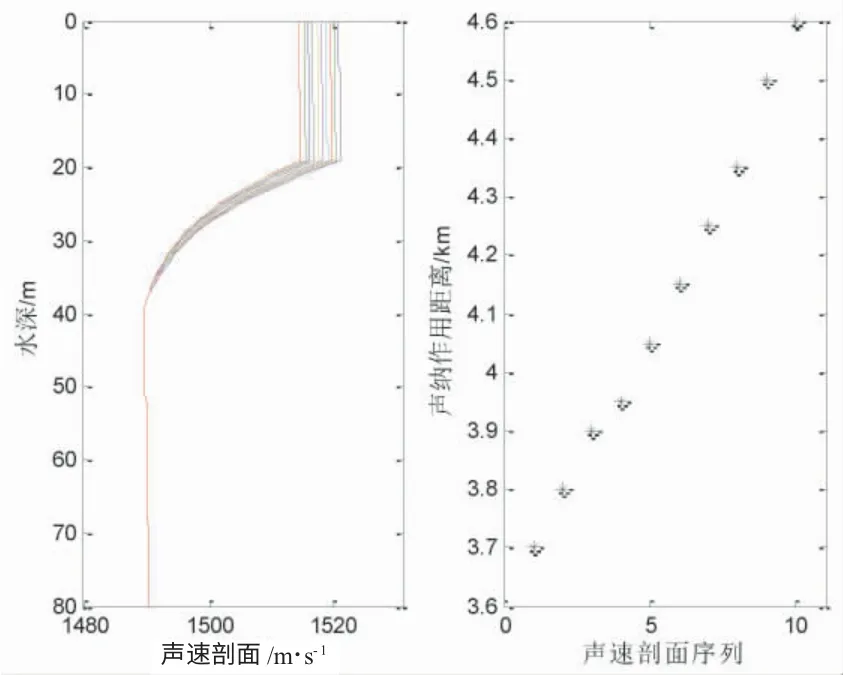
圖12 變溫度梯度變化率的聲速剖面及聲吶作用距離（接收深度40 m）

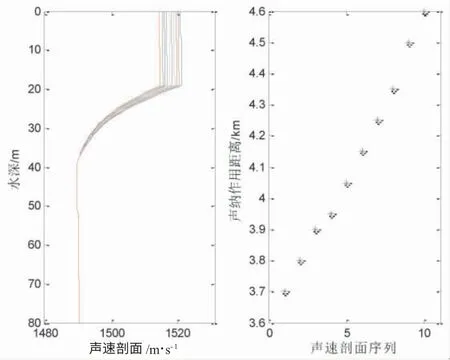
圖13 變海表溫度的聲速剖面及聲吶作用距離（聲源深度15 m）

圖14 變海表溫度的聲速剖面及聲吶作用距離（聲源深度40 m）

表7 負(fù)躍層聲速剖面下聲吶作用距離

由上分析可見(jiàn)，溫度梯度變化率和躍層上均勻?qū)拥穆曀偈怯绊懧晠茸饔镁嚯x的兩個(gè)因子，海表聲速的影響大一些。優(yōu)質(zhì)因子增大時(shí)，聲吶作用距離的最大誤差有加大的趨勢(shì)，與2.1 節(jié)研究結(jié)果類(lèi)似。

3 結(jié)論

本文針對(duì)淺海4 種不同的典型聲速剖面，通過(guò)聲速剖面的數(shù)學(xué)解析函數(shù)，選擇不同的參數(shù)取值，構(gòu)造了不同結(jié)構(gòu)的聲速剖面，結(jié)合Kraken 聲傳播模型對(duì)于聲吶作用距離進(jìn)行了仿真計(jì)算。仿真結(jié)果顯示，不同的聲速剖面的結(jié)構(gòu)變化對(duì)于聲吶作用距離的影響是不同的，其中正梯度聲速剖面的結(jié)構(gòu)變化，對(duì)于聲吶作用距離影響最大。在模擬的結(jié)果中，也顯示了對(duì)于同樣大小的誤差，海面的聲速誤差相比于海底聲速的誤差對(duì)于聲吶作用距離影響更大。對(duì)于其它頻率的情形也作了仿真，結(jié)果類(lèi)似。對(duì)于負(fù)躍層聲速剖面的結(jié)構(gòu)變化，在躍層深度不變的情況下，溫度梯度變化率和躍層以上均勻?qū)拥穆曀偈怯绊懧晠茸饔镁嚯x不確定的兩個(gè)因素。

此外，增加優(yōu)質(zhì)因子的數(shù)值仿真結(jié)果揭示了，隨著優(yōu)質(zhì)因子的增加，聲吶作用距離增大，聲吶作用距離的誤差也增大。這說(shuō)明，優(yōu)質(zhì)因子增大，除了聲吶作用距離增大，還需要注意估計(jì)的誤差也會(huì)增大。當(dāng)然，仿真不可能窮盡所有可能情形，這里給出的結(jié)果僅僅表達(dá)了論文條件下的一種認(rèn)識(shí)。但是可以確定的是，在淺海環(huán)境中，聲速剖面的結(jié)構(gòu)變化同樣會(huì)導(dǎo)致聲吶作用距離估計(jì)的誤差，這啟發(fā)研究人員，在聲吶的實(shí)際應(yīng)用中，由于聲速剖面是帶有誤差的，用一次觀(guān)測(cè)得到的聲速剖面，作為聲場(chǎng)預(yù)報(bào)的輸入，進(jìn)而確定的聲吶作用距離是不準(zhǔn)確的，更合理的做法是，還應(yīng)給出這個(gè)估計(jì)值的某個(gè)范圍，即應(yīng)該給出某個(gè)置信區(qū)間，這方面的結(jié)論還有待于理論和仿真做進(jìn)一步的詳細(xì)研究。