Fluent 兩相模型高含沙模擬需要注意的幾個問題

楊 晨 ，陳 鑫 ，薛 亮 ，孫 健

（1. 華北水利水電大學 水利學院，河南 鄭州 450046；2. 中國農業大學 水利與土木工程學院，北京 100083；3. 中國石油大學（北京） 石油工程學院，北京 102249；4. 清華大學 水沙科學與水利水電工程國家重點實驗室，北京 100084）

相對于歐美國家來看，我國河流含沙量普遍偏高，特別是北方地區，如黃河流域。另外，我國有廣大的河口海岸地區如環渤海灣、江蘇中部沿長江口至浙江北部都屬于淤泥質海岸，懸移質含沙量比較高。由于生產活動的需要，我國許多水利與海洋工程都不可避免地需要直接應用高含沙水，例如使用高含沙水吹填島礁或者用于農業灌溉，整治深水航道的疏浚維護等，即使某些應用會帶來如增加灌溉成本、損害水力機械等很多危害，因此研究高含沙條件下的水沙運動具有重要意義。隨著計算機軟硬件技術的發展，工程中比較普遍使用ANSYS 軟件模擬高含沙流動，以其中的Fluent 通用兩相流模型的應用為例，涉及的模型控制方程和紊流模型眾多，邊界條件復雜，參數不確定性極大，本文對這些問題進行了探討與研究。

1 控制方程

根據Elghobashi S E[1]的總結，水沙兩相的耦合模式按照級別從低到高可以分為單向耦合、雙向耦合和四向耦合三種類型。單向耦合模式下，泥沙顆粒對流體運動的影響被完全忽略，只需要描述顆粒在紊流中的對流擴散運動。當泥沙體積濃度達到10-6～10-3時，需要用雙向耦合模式，此時考慮了顆粒相對流體相紊動的影響。特別是顆粒自身對周邊水流繞流渦的影響，以及這種影響對顆粒運動的作用。當泥沙相濃度更高的時候，相間的相互作用需要考慮；泥沙顆粒之間的相互碰撞即碰撞效應應力變得非常重要，并且這種碰撞還強烈影響到自身以及流體的紊動特別是繞流渦，以及大量泥沙懸浮后對更多泥沙懸浮的再抑制的影響，這些因素都考慮的就是四向耦合模式。然而現有的Fluent 軟件多相流模型卻并非針對高含沙流動構建，故而需要在運用中針對此問題進行大量的二次開發，如層移輸沙問題、岸灘底層泥沙運動問題和高含沙泥漿抽取及輸送問題等。Fluent 軟件包的通用兩相流模型包括VOF 模型、混合模型和歐拉模型。VOF 模型所考慮的問題，兩相之間并沒有充分耦合，而是彼此之間有很明確的連續整段分界面分層或者自由表面流。混合模型跟VOF 方法一樣仍然使用單一流體的方法，求解混合物各種物理量的方程，不過考慮相間的滑移，由于不考慮相間作用力和顆粒粒間應力，不適合于高含沙的情況。此處討論的高含沙數值模擬是體積濃度達到10-3時的情形，適合于歐拉模型，是一種四向耦合模式。

紊流時均的相連續方程和動量方程，軟件中略去了其中紊動的時間導數項、三階紊動項、壓力梯度紊動項、應力相關紊動項，得到如下控制方程組：

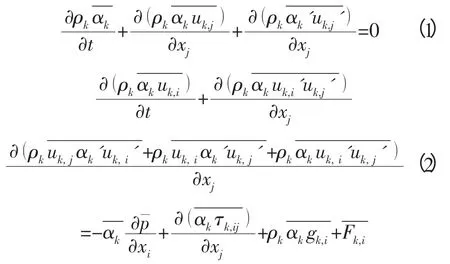
式中：下標 k 指代某一項，k=f，s；而 f 代表流體相；s 代表泥沙相；ρ 為相密度；t 代表時間；x 代表空間坐標軸；下標i,j=1，2 分別代表水平和垂直方向上的坐標，遵循愛因斯坦求和約定；u 為流速；p 為壓力；τ 為應力張量；g 為單位質量力；F 為相間作用力，它由相界面上應力的積分所得。

運用Fluent 連續介質模型，需要強調的是，模型的建立基于雙流體模型連續介質理論，只適用于高含沙濃度的情況，Hsu T 等[2]認為是泥沙體積濃度大于10-4。低濃度條件下的連續性假設不是客觀成立的，在實際問題中強行將模型運用于低濃度問題不一定能獲得收斂解，計算精度極有可能低于混合模型甚至是普通的擴散模型。此外，這個模型得到的只是兩相的濃度和運動場，并沒有方程表達單個粒子的運動，所以不能直接從此模型得到泥沙顆粒運動軌跡。

在一般濃度兩相流問題中，相界面不連續且相間作用力太過復雜，很難對這些基本方程進行封閉求解。對模型各項的物理意義理解不一樣而導致模型封閉不同，從而使得模型的最終表達式存在差異。Fluent 的紊動關聯項中，兩相體積分數與兩相速度相關項可以根據梯度輸移假定由式（3）給出，雷諾應力項可以根據Boussinesq 假設由式（4）給出。

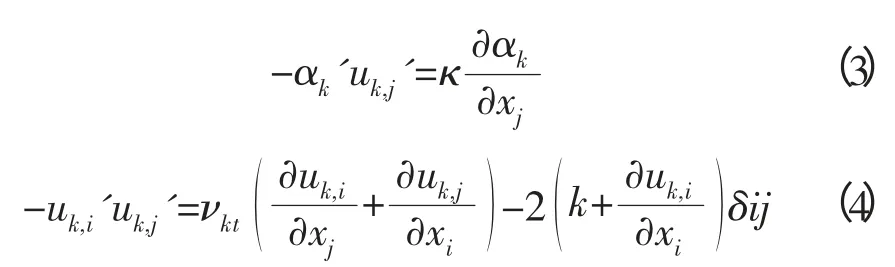
式中：κ=νst/σ 為泥沙紊動擴散系數，σ 為泥沙Schmidt 數；νft和 νst分別為流體相和泥沙相紊動粘性系數。

2 基本應力項

Fluent 通用多項模型的基礎是分子運動論，大量使用動理學理論描述泥沙相運動。Fluent 軟件完整的固體動量方程式（2）包含了固體應力項τ，只考慮平移和碰撞從顆粒的動量交換中產生的剪切和體積應力，源于 Chapman S 等[3]、Syamlal M 等[4]、Gidaspow D 等[5]學者的理論。基礎是分子運動論，多用動理學模型建模，主要運用于氣固兩相流和顆粒流。與顆粒溫度有關，隨顆粒溫度增加而增大。顆粒溫度物理意義與紊動能相同，與顆粒隨機運動的動能成比例。應力粘性包括碰撞粘性（Collisional viscosity）、動力粘度（Kinetic viscosity）、體積粘度（Bulk viscosity）和摩擦粘度（Friction viscosity）。

這些源于分子運動論和動理學理論的應力項運用于氣固兩相流和顆粒流獲得了較好的效果，但是在高含沙水流中使用仍然有待完善，因為即使紊動微弱甚至無紊動的高含沙流動中顆粒的碰撞和摩擦也是存在的。在河流海洋極限含沙區域，如底床區域，流動微弱，其適用性值得進一步商榷。此外體積粘度是顆粒壓縮和擴張的抵抗力；摩擦粘度與可壓縮機制下顆粒流動的固體壓力正相關，而固體壓力隨顆粒溫度或者是紊動能增加而增大。水沙兩相流動中的假設是泥沙顆粒不可壓縮，因此在高含沙的計算中不適合使用這兩項。

Fluent 軟件并不包含顆粒粒間應力 (Intergranular stress)，也叫離散應力(Dispersive stress)，這個是高含沙模擬的關鍵。為了獲得更貼合實際的高精度模擬結果，可考慮在二次開發中將此項編譯于源項中。Bagnold R A[6-7]最早對它進行了相關研究，其后還有 Ahilan R V 等[8]和 Fredsoe 等[9]，其等價粘性的一個基本形式如式（5）和式（6）：

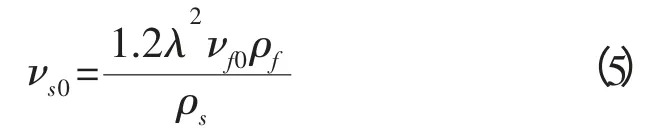
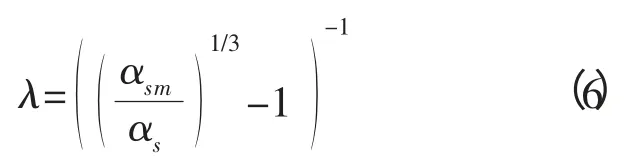
式中：λ 是泥沙相的線性濃度；αsm是泥沙相最大體積濃度，一般取值是 0.6～0.65。Liu H 等[10]、Li M等[11]、Bakhtyar R 等[12]在高濃度水沙兩相模型中充分使用并發展了粒間應力，Fluent 模擬中可考慮編譯此項。

3 紊流模型

單相流紊流模型僅有速度紊動相關項，形式相對簡單；而兩相流動量方程由于包含體積分數、壓力、速度的紊動相關項，使用的紊流模型遠遠要復雜。基于Fluent 可以使用或者二次開發的兩相紊流模型跟單相紊流一樣有很多種。在模擬高含沙水流時所有的常規紊流模型以及較為先進的大渦模擬和直接數值模擬都可以選擇使用。由于紊流理論及先進的紊流模型本身也一直在發展中，綜合考慮計算成本、穩定性、成熟性以及精度，其中最常用的是基于雙方程紊流模型的模化。無論使用何種紊流模型，在高含沙狀態下均需要合理考慮水沙的特性，特別是大量泥沙運動對水流的影響、顆粒碰撞的影響和顆粒繞流渦的影響。以經典常用的k-ε 模型為基礎，Fluent 提供了3 種方法模擬多相流中的紊流。不過其既有兩相紊流模型主要源于氣固兩相流動，有關固體相的紊動理論主要依靠分子運動論，在水沙兩相流動中的適用性值得進一步完善。

最完整和容易理解的是每相紊流模型（Turbulence Model for Each Phase）。它為水相和泥沙相都求解一套k 和ε 輸運方程。同時考慮體積分數、壓力和流速的紊動后，兩相流動方程按雷諾展開平均后推導所得到的紊動能方程和紊動能耗散率項數非常大[13]，分別具有三十多項和六十多項。當紊流傳遞在相間起重要作用時，這個紊流模型是合適的選擇。然而此模型需要模化參數太多，計算成本巨大并且不易收斂，還有待進一步發展以提高結果的可靠性，周立行[14]進行了大量研究。考慮到兩相最大速度差一般不會超過最大流速2%[11]，在高含沙水流動模擬中的應用需要慎重考慮。

Fluent 默認的是混合紊流模型（Mixture Turbulence Model）。它源于混合動量方程的時均化，僅求解混合物共同的k-ε 方程，一般認為它適合于相分離、分層或接近分層的多相流，或者兩相之間的密度比接近1 的情況。不去考慮泥沙相跟水相紊動區別的情形下，使用混合屬性和混合速度捕獲紊流的重要特征是足夠的。比較理想的運用情況是泥沙相的濃度不會太高，在一般的水力機械問題里面應當是合適的；而在河流海洋具有低床的情形，由于床面附近含沙濃度達到了極限狀態，模擬效果會差很多。

最普通的是分散紊流模型（Dispersed Turbulence Model）。對水相使用k-ε 方程求解，在此基礎上采用顆粒追隨理論獲得泥沙相紊動特征。這種情形下，對泥沙相隨機運動的起支配作用的是水相紊流的影響，顆粒間的碰撞可忽略。此時泥沙相的紊動量根據水相的平均特征、顆粒弛豫時間和粒子相互作用時間的旋渦給出。當明顯地水相是主要連續相而泥沙相是分散稀釋的第二相時，這個模型是比較適用的。總體上看水力機械中很多高含沙水流都是屬于這種情形，再考慮到此模型相對成熟和完善，計算成本不大，因此采用此模型用于水力機械高含沙水流計算是比較合適的。

關于紊流模型，還需要注意到高含沙濃度對水流紊動的抑制作用。Elghobashi S E 等[13]最初紊流模型包含體積紊動相關量，但并沒有具體應用于高含沙問題，其參數也沒有含沙影響。大量兩相模型不直接計算高濃度處的紊動能量和耗散率，而像單相流動利用壁函數在底部一定高度給定高含沙條件下的紊動能和紊動能耗散率[12，15-16]。

4 邊界條件

水相的邊界條件中，最需要注意的是壁面邊界條件。傳統的壁函數表達式僅僅適合于清水狀況，與泥沙（粒徑、濃度）沒有關系。當大量泥沙存在時，粗糙高度、粘性底層和過渡層的厚度都會發生較大的變化；流速分布跟清水條件下的分布也有很大不同，如圖 1 所示[17]。其中：uf與式（1）一樣代表水相流速；u*代表摩阻流速；y' 代表相對水深，y'=0 為水底，y'=1 為水面。而壁面邊界條件的選擇又極大影響紊流模型及動量方程的求解精度，然后影響泥沙擴散系數和濃度分布計算的精度，最終影響的是泥沙輸送率的估計。關于這方面的論著已有不少[18-20]，可以考慮將最先進的成果用于Fluent 高含沙模擬中，改善數值結果。

泥沙相的邊界條件，最大的問題是現有的泥沙運動理論體系都源于恒定流動，在考慮時間變化時并非總是適用的，極有可能給計算結果帶來巨大誤差。以周期性的流動為例，見圖2 二階Stokes 波流動過程中層移輸沙問題泥沙參考濃度的變化過程：點代表實驗值，點畫線和虛線代表兩個經典恒定流動公式，實線代表非恒定流動理論推導的理論解[21]，t 即式（1）的時間；T 代表二階 Stokes 波流動的周期。傳統恒定流動的邊界條件不受相位差影響，在流動轉向時候t/T～0.42 瞬時流速很小，根據經典的Engelund F 等[22]和 Zyserman J A 等[23]公式（即圖 2中EF76 和ZF94）獲得的參考濃度很小，而實際情況下已懸浮泥沙含量來不及沉降會保持一定的數值；不考慮大量已懸浮泥沙對再懸浮的抑制，兩個經典公式的解隨著流動速度增加一直增長到很大的水平t/T～0.21，與實驗背離。揚沙率或者挾沙能力等泥沙參數的變化也跟參考濃度類似。由于現實中大部分流動都是時間變化的非恒定流動，因此可以考慮在運用Fluent 軟件時重新編譯泥沙邊界條件。

5 結論

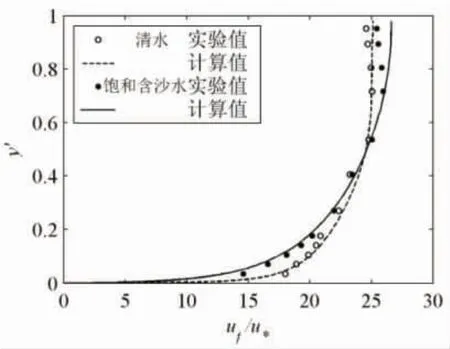
圖1 清水和飽和含沙水流速分布

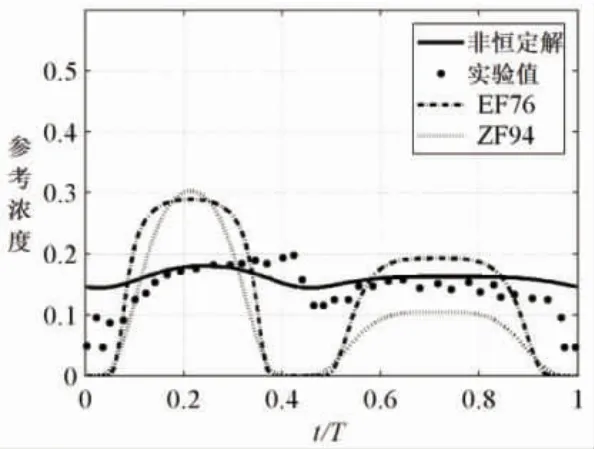
圖2 非恒定流動中泥沙濃度邊界條件

高含沙兩相流動的精確數值模擬在我國水利工程中具有重要的意義。本文針對較為普遍使用的Fluent 商業軟件通用兩相模型，在控制方程、基本應力項、紊流模型和邊界條件這幾個要素的比選上展開了討論。在此基礎上本文提出了在軟件模擬仿真中可能出現問題的原因及改進的方向，并期望Fluent 軟件在高含沙流動模擬這方面能得到更好的發展和應用。