用動態畫板實現超聲波反射、折射和波形轉換的動態演示

徐平軍

【摘? 要】通過應用GeoGebra動態畫板演示了超聲波的反射、折射和波形轉換的動態演示，設置了鋼軌超聲波探傷中常用的探頭入射角、介質聲速等參數，生動直觀地展示了這些參數對反射、折射、波形轉換的影響。

【關鍵詞】鋼軌超聲波探傷;反射;折射;波形轉換;動態畫板;GeoGebra

1 簡介

無損檢測是鋼軌探傷工的基礎課，超聲波的反射、折射和波形轉換是其中難點之一，其原理復雜、抽象、理論性強，我們新職工在學習中往往不容易掌握，本文以超聲波平面波為例，通過GeoGebra的動態演示了平面波在平面、曲面上的各種狀態，將抽象的理論變得形象，將籠統的知識點變得直觀，幫助學員能很好地掌握知識點。

2 超聲波在平面上反射過程

2.1 反射的定義：超聲波從一種介質傳播到另一種介質時，在兩種介質的分界面上，部分能量反射回原介質內，這種現象稱為反射。界面上這種聲能（聲壓、聲強）的分配和傳播方向的變化都遵循一定的規律。

2.2 操作過程

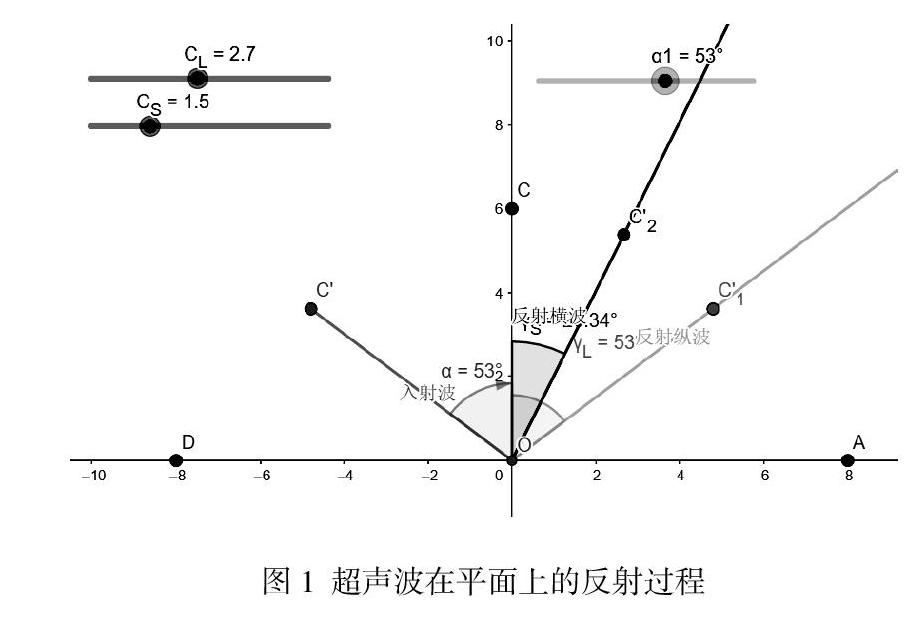
（1）如圖1為一入射縱波經CO入射至AD界面上，形成OC₁的反射縱波。假設入射角為α1，縱波反射角為γ_L，第一介質縱波聲速為C_L，根據折射定律sinα1/C_L=sinγ_L/C_L，γ_L=sin^-1（C_Lsin（α1）/ C_L）。

（2）在x-y坐標系中，如圖2選擇描點工具建立原點O，在x軸上建立A、D點，做直線AD表示界面，在y軸上建立B、C點，經B、C點做一條法線。如圖3建立滑動條α1，類型為角度，最小值為0°，最大值為90°，增量為0.1°。

（3）如圖4選擇軸對稱的旋轉功能繪制一個以O為旋轉中心，以C為對象旋轉了α1的點C，做線段CO代表入射波，標示∠COC為入射角α。選擇旋轉工具，以O為旋轉中心，以C為對象旋轉了sin^-1（C_Lsin（α1）/ C_L）的點C₁，標示∠CO C1為反射角γ_L，做射線O C1代表反射縱波。

（3）如圖5選擇旋轉工具，以O為旋轉中心，以C為對象旋轉了sin^-1（C_Ssin（α1）/ C_L）的點C₂，標示∠CO C2為反射角γ_S，做射線O C2代表反射橫波。

（4）橫波入射時過程類似，不再贅述。

（5）拉動滑動條α1，使入射角α在0°-90°之間變化，入射波和反射波也會隨之變化。

3 超聲波在平面上的折射過程

3.1 折射的定義：超聲波從一種介質傳播到另一種介質時，在兩種介質的分界面上，有有部分能力透過界面進入另一種介質，這種現象稱為折射。界面上這種聲能（聲壓、聲強）的分配和傳播方向的變化都遵循一定的規律。

3.2 操作過程

（1）如圖6為一入射縱波經CO入射至AD界面上，形成OC₃的反射縱波和OC₄折射橫波。假設縱波折射角為β_L，橫波折射角為β_S，第二介質縱波聲速為C_L2，第二介質縱波聲速為C_S2，根據折射定律sinα1/C_L=sinβ_L/ C_L2=sinβ_S/ C_S2，β_L=sin^-1（C_L2 sin（α1）/ C_L），β_S=sin^-1（C_S2 sin（α1）/ C_L）。

（2）前面步驟參考2.2。如圖7選擇軸對稱的旋轉功能繪制一個以O為旋轉中心，以C為對象旋轉了角度為β_L的點C₃，標示∠BO C₃為縱波折射角β_L，做射線O C₃代表折射縱波。

（3）如圖8選擇旋轉工具，以O為旋轉中心，以C為對象旋轉了角度為β_S的點C₄，標示∠BO C₄為橫波折射角β_S，做射線O C₄代表折射橫波。

（4）橫波入射時過程類似，要注意的是需合理設置第二介質中的聲速，必須使得sin值在-1至1之間，否則將不會產生折射波，詳細過程不再贅述。

（5）拉動滑動條α1，使入射角α在0°-90°之間變化，入射波和折射波也會隨之變化。

4 超聲波傾斜入射至異質平界面時產生的臨界角

臨界角是特殊的入射角，在鋼軌超聲波探傷中具有很重要的意義。

4.1 臨界角的概念：當C_L2 > C_L1，則β_L=90°時對應的縱波入射角稱為第一臨界角，用α_Ⅰ表示。若C_S2 > C_L1，則β_S= 90°時對應的縱波入射角稱為第二臨界角，用α_Ⅱ表示。當γ_L= 90°時，對應的橫波入射角稱為第三臨界角，用α_Ⅲ表示。表1為鋼軌探傷中常用的臨界角。第一介質中的縱波入射角α_L<α_Ⅰ，則第二介質中既存在折射橫波，又存在折射縱波，如圖9所示。若α_L=α_Ⅰ～α_Ⅱ，則第二介質中只存在折射橫波，不存在折射縱波。當第一介質為固體時，橫波入射時，若α_S≥α_Ⅲ才會有第三臨界角，此時第一介質中只有反射橫波，沒有反射縱波。鋼軌探傷中37?探頭檢測軌底橫向裂紋具有非常好的檢測效果，就是因為橫波入射角α_S≥α_Ⅲ的緣故，此時反射橫波很強，且與裂紋的長度無關。

4.2 操作過程

（1）前面步驟參考3.2。假設縱波折射角為β_L，橫波折射角為β_S，第一介質為有機玻璃縱波聲速為2730m/s，第二介質為鋼，縱波聲速為5900m/s，橫波聲速為3230m/s。建立3個按鈕，標題分別是第一臨界角、第二臨界角、第三臨界角。根據折射定律可得α_Ⅰ=sin^-1（2730/5900 sin（α1））=27.6°，α_Ⅱ=sin^-1（2730/3230 sin（α1））=57.7°，α_Ⅲ=sin^-1（3230/5900 sin（α1））=33.2°。

（2）調到第一臨界角按鈕的設置界面，在腳本里輸入C_L=2730m/s，C_L2=5900m/s，CS2=3230m/s，α1=27.6°。第二臨界角按鈕的腳本中輸入相同內容，并把α1改為57.7°。

（3）由于第三臨界角是固體介質中橫波入射的情況，所以需要增加新的參數設置，并增加反射路徑，過程可參考3.2。調到第三臨界角按鈕的設置界面，在腳本里輸入C_L=3230m/s，C_L=5900m/s，C_S=3230m/s，α1=33.2°。

（4）點擊3個按鈕就能直接觀察到臨界角的對折射波或反射波的影響。

5 超聲波在彎曲界面上的反射和折射過程

5.1 當超聲波入射到彎曲界面上時，其反射波將發生聚集或反射，如圖4、5所示。波束與曲面上各入射點的法線成不同的夾角，入射角為0的聲束沿原方向返回，其余聲束的反射則隨著距聲軸距離的增大，反射角逐漸增大。曲面的凹凸按從發射方向看進行區分，當曲面為凹面時，反射波發生聚焦;曲面為凸面時，反射波向四周發散。

5.2 平面波入射于球面上產生球面反射波，在柱面上則產生柱面反射波，其反射聲壓可根據焦距f進行計算。當超聲波入射至彎曲界面上使，其折射波同樣會發生聚集和發散，圖11、12所示是以鋼/水為例說明了四種情況。

5.3 操作過程參考2.2。

6結語

本文采用GeoGebra對超聲波的反射、折射和波形轉換進行了動態繪圖演示，同時設置了入射角、聲速、臨界角等參數，使學員能夠直觀的觀察反射、折射及波形轉換的過程，使得原來復雜抽象的理論知識變得生動形象，促進了他們對超聲波理論知識的理解和掌握。

參考文獻：

[1]鐵路職工崗位培訓教材編審委員會.鋼軌探傷工.北京：中國鐵道出版社，2014.

[2]王洪濤 石禮偉 李艷.用GeoGebra實現反射折射及雙折射的惠更斯原理繪圖.物理教師，2019，40（5）：75-77.