優化參考答案 發揮導向作用

白雪峰 宋月娟 任媛媛

[摘? 要] 文章基于一道中考數學試題多種解題方法的比較研究，闡明了參考答案的價值和作用，結合中考復習解題教學改進的實際需求，提出了在教學評價中編制和使用參考答案的具體策略與要求.

[關鍵詞] 參考答案;導向作用;中考數學試題;一題多解;比較研究

教學評價既是整體教學理念的引導，又是教學理念變化的反映，而評價的標準是整個評價的核心 [1]. 因此， 從標準的變化中我們可以看出教學理念的變化. 在各種考試評價中，都會提供參考答案，因此，參考答案對師生來說都是非常熟悉的. 在使用參考答案的過程中，師生都能感受到參考答案帶來的便利：明確了數學表達的規范格式，有助于指導學生養成良好的書寫習慣;提供了便于學生及時自我反饋檢測情況的參考依據，有助于學生及時糾正錯誤;呈現了解題思路和主要方法，有助于教師備課，節省了時間等等[2] . 但是，由于使用參考答案不當以及參考答案自身存在一些缺陷，也帶來了一些問題，使得參考答案失去了指導教學改進的導向功能，以及拓展師生解題思路、發現數學內容本質的實踐價值. 本文以2019年成都市中考數學第19題為例，闡明了筆者對發揮參考答案價值導向作用的思考與實踐，以期和同仁分享.

問題與解析

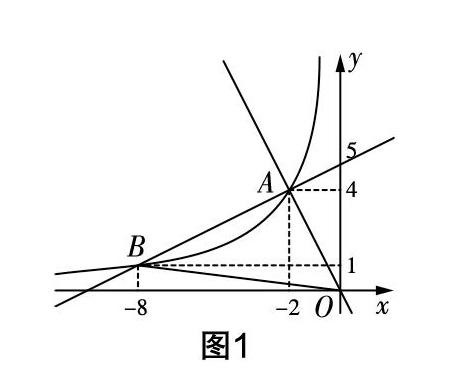
如圖1，在平面直角坐標系xOy中，一次函數y=■x+5和y=-2x的圖像相交于點A，反比例函數y=■的圖像經過點A.

（1）求反比例函數的解析表達式;

（2）設一次函數y=■x+5與反比例函數y=■的圖像交于點B，連接OB，求△AOB的面積.

我們知道，在平面直角坐標系中，點的坐標是這樣定義的：設A是平面直角坐標系上的一點，過點A作x軸的垂線AM，作y軸的垂線AN，M，N是垂足，則點M在x軸的坐標m和點N在y軸的坐標n一起，記作（m，n），叫作點A在平面直角坐標系上的坐標，簡稱點A的坐標，記作A（m，n），垂線段AM=m，AN=n.有了這樣的理解，如果知道在平面直角坐標系內的三點A，B，C的坐標，那么求△ABC的面積就不必死記硬背那些所謂的公式，應用AM，AN為高線，依據“補形法”便可順暢求解△ABC的面積.

■ 多解與比較

如圖1，（1）由y=■x+5，y=-2x解得x=-2，y=4.所以點A的坐標為（-2，4）. 將（-2，4）代入y=■，得到a=-8. 所以反比例函數的表達式為y=-■.

（2）由y=■x+5，y=-■解得x=-2，y=4或x=-8，y=1. 所以B（-8，1）.在△ABO中，點A，B，O的坐標分別為A（-2，4），B（-8，1），O（0，0）.

下面來求△ABO的面積.

筆者認為，求一個三角形的面積，一般來說可以考慮從以下三個角度入手：第一，考慮這個三角形是否可直接求面積，即是否可以直接求出此三角形的一邊及這一邊上的高;第二，考慮能否將原三角形看成幾個易求面積的三角形的和或者差;第三，考慮將原三角形轉化為其他易求的等面積的圖形來解決. 實際上，本題中的三角形或可補成其他圖形以間接求其面積，但是一般來說，補成的圖形邊數越多，圖形就會越復雜，求解相對也更加困難. 這里僅舉幾例，旨在說明方法，有興趣的讀者可以做更多嘗試.

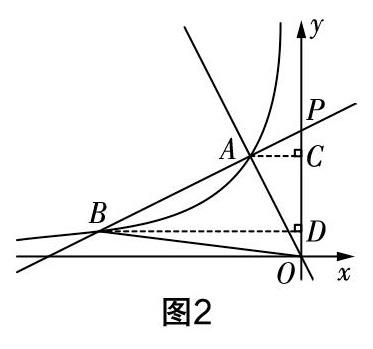
解法1?如圖2，直線AB：y=■x+5與y軸交于點（0，5），即在y軸上的截距為5，所以 OP=5，過點A，B分別作y軸的垂線AC，BD，垂足為C，D.

因為點A，B的坐標分別為（-2，4），（-8，1），所以 AC=2，BD=8. 所以S△ABO=S△BOP-S△AOP=■OP·BD-■OP·AC？搖=■OP·（BD-AC）=■×5×（8-2）=15.

說明解法1從直線AB與y軸相交這個條件出發，發現△ABO面積是△BOP與△AOP面積的差，且△BOP與△AOP有公共邊OP，OP易求且長度為5.

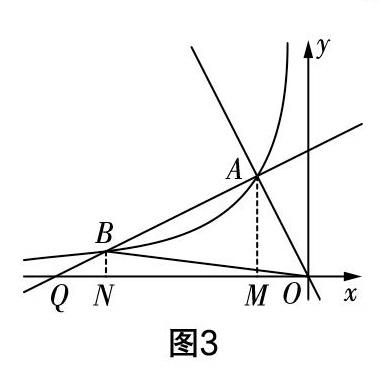
解法2?類似于解法1，如圖3，直線AB：y=■x+5在x軸上的截距為-10，所以OQ=10. 過點A，B分別作x軸的垂線AM，BN，垂足為M，N. S△ABO=S△AOQ-S△BOQ=15.

說明?解法2是從直線AB與x軸相交這個條件出發，將△ABO面積看成是△AOQ與△BOQ面積的差，借助于A，B，Q三點坐標求解. 解法2相較于解法1，需先求出Q的坐標，計算量略微增多，難度也略有增加.

解法3?如圖4，過點A，B分別作x軸的垂線AM，BN，垂足為M，N. 由模型可知： S△ABO=S梯形AMNB. 所以S△ABO =■（y1+y2）（x1-x2）=■（1+4）[（-2）-（-8）] =■×5×6=15.

說明?實際上，在解法3中，應用反比例函數 y=-■解析式得x·y=-8，所以x·y=8，所以S△AOM =S△BON=4. 去掉其公共部分的△POM，S△AOP =S梯形BNMP，應用題目中反比例函數圖像及其特殊的性質，割去△MOP而補成梯形BNMP，這種解法計算難度不大，不過對于學生來說不易想到.

解法4?如圖5，過點A，B分別作y軸、x軸的垂線AM，BN，垂足為M，N，設AM，BN交于點Q. 這樣所求△ABO的面積就轉化為從矩形MONQ的面積中，減去三個三角形，即減去△AOM、△BON和△ABQ 的面積.

說明?解法3和解法4采用的都是典型的“割補法”，其中解法3是將△ABO補成梯形進行求解，而解法4則是將△ABO補成矩形進行求解. 應該說，解題思路是比較簡單的，但計算量較解法1和2有所增加.

解法5?如圖6，因為點B（-8，1），所以直線BO：y=-■x.

過點A作AN⊥x軸，垂足為N，且交BO于點C，則yC=■. 所以 S△ABO=■AC·（xO-xB）=■4-■（0+8）=15.

說明?實際上，我們還可以拆分△ABO成兩個具有公共邊的三角形. 如圖6，如果過點B作AN的垂線，垂足為M. 作BP垂直x軸于點P，OP=8. 這樣原△ABO被分成兩個三角形△ABC和△AOC，公共邊為AC. 所以S△ABO = S△ABC+S△AOC=■AC·BM+■AC·ON=■AC·（BM+ON）=■AC·OP=15.

解法6?如圖7，因為點B的坐標為（-8，1）. 過點B作BC⊥y軸于點C，交AO于點D. 將y=1代入y=-2x，解得x=-■. 所以D-■，1，所以BD=■. 所以S△ABO=■×■×4=15.

說明在上述解法中，基于過點B作垂直于y軸的直線，將△ABO分成了兩個三角形△ABD和△BOD，且兩個三角形具有公共邊為BD. 實際上，如圖7，我們還可以過點A作AF⊥x軸于點F，與BD交于點E，則EF=OC. 于是S△ABO=S△ABD+S△BOD=■BD·AE+■BD·OC=■BD·AE+■BD·EF=■BD·AF. 即S△ABO =■BD（yA-yO）=15.

事實上，筆者認為解法5和解法6都是通過分割△ABO求得結果，解題中所產生的計算既復雜又不易理解，不如利用點A，B的坐標和補形法相結合而產生的解法1和解法2來得簡單. 實踐出真知，數學的解題也是如此.

解法7 如圖8，過點B作BC∥OA，可設直線BC的解析表達式為y=-2x+b，且過點（-8，1），易求b=-15，所以可得直線BC：y=-2x-15. 直線BC與x軸的交點為（-7.5，0）. 所以S△AOB=S△AOC=■OC·yA=■×7.5×4=15.

解法8?類似地，如圖9，如果過點A作AC∥OB，并設直線AC的解析表達式為y=-■x+b，由于AC過點（-2，4），則可得直線AC的解析表達式為y=-■x+■，它與y軸的交點為0，■. 進一步由S△AOB=S△BOC求解.

說明? 在解法8中，直線OB的解析式題目中沒有直接給出，需要學生自己求解，相較于解法7略為復雜，感興趣的讀者可自行完成計算.

解法9?由直線AB的解析式y=■x+5得kAB=■，由直線OA的解析式y=-2x得kOA=-2.

因為 kAB·kOA=-2×■=-1，所以OA⊥AB. 所以△OAB為直角三角形. 經計算得OA=■=2■，AB=■=3■，所以 S△ABO=■OA·AB=■×2■×3■=15.

說明?從直線AB與直線OA的解析式可以發現kAB·kOA=-2×■=-1，根據解析幾何知識：如果直線l1的解析式為y=k1x+b1，直線l2的解析式為y=k2x+b2，同時k1，k2存在且k1k2≠0，那么k1=-■？圳l1⊥l2 . 可知△ABO為直角三角形，因此可以直接求這個三角形的面積. 但是，這個條件相較于圖形信息而言較為隱秘，不容易被發現.

另外，在函數與幾何結合的綜合題中，兩條直線平行或垂直的問題屬于常見問題. 在初三專題復習過程中，教師可以結合學生實際，在不增加學生學習負擔的情況下，把部分解析幾何的內容介紹給考生，并指導學生進行解題實踐，這也是一種值得提倡的做法. 有了以上公式，學生再遇到垂直和平行的問題，應用上述公式便可使“直線型”問題得到順暢而簡明的解決.

縱觀上述解法，可以發現，解法1至4采用的都是“補形”的方法，通過借助顯性的已知條件，將所求圖形“轉化”為易求面積的特殊圖形，再用補成的大圖形減去相應小圖形從而得解. 此種方法選取的條件信息最為直觀，計算比較簡單，計算量略有區別，蘊含其中的重要數學思想就是“化歸”的思想. 解法5、6對學生的數學能力有更高要求，需要借助已知條件合理“分割”這個三角形，然后再用分割圖形的面積和來求解：比如，可以作平行于x軸的輔助線進行橫向拆分或者作平行于y軸的輔助線縱向拆分;再如，可以過點A作輔助線拆分，或者過點B作輔助線. 當然，還需要學生理解平面內與坐標軸平行的直線上兩點間的距離公式AB=x1-x2或CD=y1-y2. 而解法7、8主要利用轉化思想，通過作△ABO中某一邊的平行線，將原三角形問題轉化為邊落在坐標軸上的三角形的面積，這種方法對學生的能力要求更高，需要將函數解析式、幾何圖形之間的關系、坐標的運用綜合思考，確實需要有較高站位才能實現這種解法的突破. 在上述解法中，解法9很好地利用了隱含條件kAB·kOA=-1，屬于特殊解法，不具有一般性.

■ 實踐與思考

縱觀上述四類九種解法，基于比較研究不難發現：在坐標系下解決問題，如何將點的坐標轉化為線段長，是解題關鍵. 根據點坐標的定義，必然需要作平行（或垂直）于坐標軸的直線，據此產生多種思路，也是基于利用坐標轉化成線段長的方法，將轉化后的圖形與所給坐標或可求點的坐標相互關聯，通俗地說就是過已知點（或易求點）作平行（或垂直）于坐標軸的直線，從而實現圖形的“割”或“補”. 另外值得一提的是，解法5和 6是不同教輔材料中給出的參考答案，而其他解法都是筆者在教學實踐中收集整理的. 應該說每種解法都有它的優勢，學生在運用中也會存在一些障礙點. 在具體的教學中，教師還要根據學生的認知基礎、接受程度和發展要求以及復習教學實際，適當展開對解題方法的研討，因材施教效果才會更佳.

1. 把握數學本質，提供典型解題方法

在解題教學中，教師如果固守參考答案所提供的思路或解法，在試題講解中就會被局限，學生也就會缺乏靈活而創新的解題能力，甚至會因為解題思路窄化而“碰壁”. 事實上，參考答案不一定是標準答案，不一定就是最優、最簡的解法，教師在使用參考答案時必須要有自己的思考，不能過分依賴參考答案. 在實際解題教學中，教師要善于基于學生，更要善于發展學生.